字符子串和字符子序列的区别
字符字串指的是字符串中连续的n个字符;如palindrome中,pa,alind,drome等都属于它的字串
而字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符;如palindrome中,plind,lime属于它的子序列,而mod,rope则不是,因为它们与字符串的字符顺序不一致。
Manacher's Algorithm
在计算机科学中,最长回文子串或最长对称因子问题是在一个字符串中查找一个最长的连续的回文的子串,例如“banana”最长回文子串是“anana”。最长回文子串并不一定是唯一的,比如“abracadabra”,没有超过3的回文子串,但是有两个回文字串长度都是3:“ada”和“aca”。在一些应用中,我们求出全部的极大回文子串(不被其他回文串包含的回文子串)。
Manacher于[1]发现了一种线性时间算法,可以在列出给定字符串中从任意位置开始的所有回文子串。并且,Apostolico, Breslauer & Galil [2]发现,同样的算法也可以在任意位置查找全部极大回文子串,并且时间复杂度是线性的。因此,他们提供了一种时间复杂度为线性的最长回文子串解法。另外,Jeuring (1994)[3], Gusfield (1997)[4]发现了基于后缀树的算法。也存在已知的高效并行算法。
最长回文子串算法不应当与最长回文子序列算法混淆。
要在线性时间内找出字符串的最长回文子串,这个算法必须利用回文和子回文的这些特点和观察
C++实现
constexpr auto MAXN = (int)7000000; char s[MAXN << 1], str[MAXN]; int RL[MAXN]; int Manacher(void) { size_t len = strlen(str); *s = '#'; for (int i = 0; i < len; i++) { s[(i << 1) + 1] = str[i]; s[(i << 1) + 2] = '#'; }len = (len << 1) + 1; int max = 1, pos, maxRight = -1; memset(RL, 0, sizeof(RL)); for (int i = 0; i < len; i++) { if (i < maxRight) RL[i] = std::min(RL[(pos << 1) - i], maxRight - i); else RL[i] = 1; while (i - RL[i] >= 0 && i + RL[i] < len && s[i - RL[i]] == s[i + RL[i]])++RL[i]; if (i + RL[i] > maxRight) { pos = i; maxRight = i + RL[i]; } max = std::max(max, RL[i] - 1); } return max; }
具体实现过程演示
#include<cstring> #include<cstdio> #include<iostream> #include<algorithm> #include<cmath> #include<queue> #define lson l,mid,idx<<1 #define rson mid+1,r,idx<<1|1 #define lc idx<<1 #define rc idx<<1|1 #define N 100010 #define ll long long using namespace std; char str[N],s[N]; int len[N]={0}; int manachr(){ s[0]='$'; int n=1; for(int i=0;str[i];i++)s[n++]='#',s[n++]=str[i]; s[n++]='#';s[n]='�'; int MAX=0,id=0,mix=0; for(int i=1;i<n;i++){ if(i<mix)len[i]=min(len[2*id-i],mix-i); else len[i]=1; while(s[i-len[i]]==s[i+len[i]])len[i]++; if(len[i]+i>mix)mix=len[i]+i,id=i,MAX=max(MAX,len[i]); } for(int i=1;i<n;i++)printf("len[%d]=%d ",i,len[i]); return MAX-1; } //mix 为id为中心 回文串最右端 当i<mix 时 // 利用回文串的性质 len[i]=len[id-(i-id)] 考虑到i会超过mix 和mix-i取最小 // int main(int argc, char const *argv[]) { cin >> str; cout << manachr() << endl; return 0; }
MATLAB实现
function m = Manacher(a) T = ['$#' reshape([a;ones(size(a))*'#'], 1, '') '@']; l = length(T); P = zeros(1, l); mx = 0; %range id = 0; %center for i = 2:l-1 if i < mx P(i) = min(P(2 * id - i), mx - i); else P(i) = 1; end while T(i+P(i)) == T(i-P(i)) P(i) = P(i) + 1; end if P(i) + i > mx mx = P(i) + i; id = i; end end m = max(P)-1;
最长回文子序列
分析
对任意字符串,如果头和尾相同,那么它的最长回文子序列一定是去头去尾之后的部分的最长回文子序列加上头和尾。如果头和尾不同,那么它的最长回文子序列是去头的部分的最长回文子序列和去尾的部分的最长回文子序列的较长的那一个。
str[0...n-1]是给定的字符串序列,长度为n,假设f(0,n-1)表示序列str[0...n-1]的最长回文子序列的长度。
1.如果str的最后一个元素和第一个元素是相同的,则有:f(0,n-1)=f(1,n-2)+2;例如字符串序列“AABACACBA”,第一个元素和最后一个元素相同,其中f(1,n-2)表示红色部分的最长回文子序列的长度;
2.如果str的最后一个元素和第一个元素是不相同的,则有:f(0,n-1)=max(f(1,n-1),f(0,n-2));例如字符串序列“ABACACB”,其中f(1,n-1)表示去掉第一元素的子序列,f(0,n-2)表示去掉最后一个元素的子序列。
设字符串为s,f(i,j)表示s[i..j]的最长回文子序列。
状态转移方程如下:
当i>j时,f(i,j)=0。
当i=j时,f(i,j)=1。
当i<j并且s[i]=s[j]时,f(i,j)=f(i+1,j-1)+2。
当i<j并且s[i]≠s[j]时,f(i,j)=max( f(i,j-1), f(i+1,j) )。
由于f(i,j)依赖i+1,所以循环计算的时候,第一维必须倒过来计算,从s.length()-1到0。
最后,s的最长回文子序列长度为f(0, s.length()-1)。
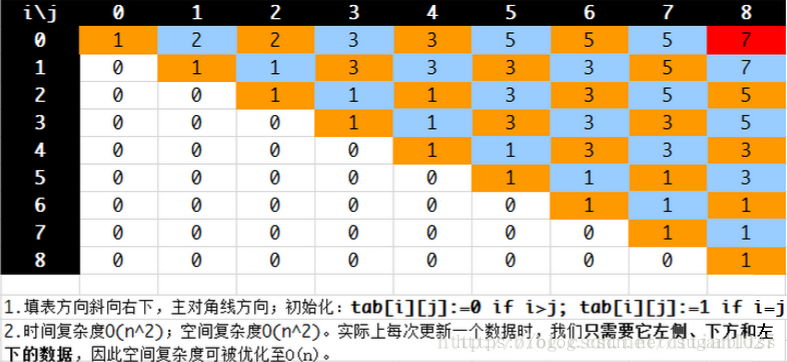
以"BBABCBCAB"为例:
(注:本程序的填表方向斜向左上,即每次从最后一行最后一个数开始,依次向左填写)
C++实现
int dp[1005][1005]; char str[N]; // dp[i][j] 代表 str[i]到str[j] 中回文子序列的最大长度 // str[i]==str[j] dp[i][j]=dp[i+1][j-1]+2; // str[i]!=str[j] dp[i][j]=max(dp[i][j-1],dp[i+1][j]); int main(){ cin>>(str+1); int n=strlen(str+1); for(int i=n;i>=1;i--){ dp[i][i]=1; for(int j=i+1;j<=n;j++){ if(str[i]==str[j])dp[i][j]=dp[i+1][j-1]+2; else dp[i][j]=max(dp[i+1][j],dp[i][j-1]); } } cout<<dp[1][n]<<endl; }
为进一步减小空间复杂度,我们发现计算第i行时只用到了第i+1行,这样我们便不需要n行,只需要2行即可。
滚动数组优化
#include <iostream> #include <bits/stdc++.h> using namespace std; int dp[2][1500]; int main() { string str; while(cin >> str) { int len = str.length(); memset(dp,0,sizeof(dp)); int cur = 0; for(int i = len - 1; i >= 0; i--) { cur ^= 1; dp[cur][i] = 1; for(int j = i + 1; j < len; j++) { if(str[i] == str[j]) dp[cur][j] = dp[cur^1][j-1] + 2; else dp[cur][j] = max(dp[cur][j-1],dp[cur^1][j]); } } cout<<dp[cur][len-1]<<endl; } }