在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以tree来表示。
用途
维护一个无向图的连通性,判断n个点m条边时最少加多少边可以连通所有点
判断在一个无向图中,两点间加边是否会产生环(最小生成树克鲁斯卡尔中有用到)
维护集合等操作
操作
(1)Union(Root1, Root2):把子集合Root2并入集合Root1中。要求这两个集合互不相交,否则不执行合并。
(2)Find(x):搜索单元素x所在的集合,并返回该集合的名字。
(3)UnionFindSets(s):构造函数,将并查集中s个元素初始化为s个只有一个单元素的子集合。
初始化
用数组来建立一个并查集,数组下标代表元素,下标对应的值代表父节点,全部初始化为-1,根节点为一个集合的元素个数,数组的长度为并查集的初始连通分量的个数。并查集要求各集合是不相交的,因此要求x没有在其他集合中出现过。算法如下:
//构造函数
UF(int size){ this->count = size; array = new int[size]; for(int i = 0 ; i < size ; i++){ this->array[i] = -1; } }
查找操作
返回能代表x所在集合的节点,通常返回x所在集合的根节点。这里的查找操作通常采用路径压缩的办法,即在查找过程中组不减小树的高度,把元素逐步指向一开始的根节点。这样下次再找根节点的时间复杂度会变成o(1)。如下图所示
算法如下:
//查找操作,路径压缩
int Find(int x){ if(this->array[x] < 0){ return x; }else{ //首先查找x的父节点array[x],然后把根变成array[x],之后再返回根 return this->array[x] = Find(this->array[x]); } }
并操作
将包含x,y的动态集合合并为一个新的集合。合并两个集合的关键是找到两个集合的根节点,如果两个根节点相同则不用合并;如果不同,则需要合并。
这里对并操作有两种优化:根节点存树高的相反数或者根节点存集合的个数的相反数,这两种方法统称按秩归并。通常选用第二种方法。
归并过程如下图:
算法如下:
//并操作,跟结点存储集合元素个数的负数
//通过对根结点的比较
void Uion(int root1, int root2){ root1 = this->Find(root1); root2 = this->Find(root2); if(root1 == root2){ return; }else if(this->array[root1] < this->array[root2]){ //root1所代表的集合的个数大于root2所代表集合的个数 //因为为存放的是元素个数的负数 this->array[root1] += this->array[root2]; this->array[root2] = root1; count--; }else{ this->array[root2] += this->array[root1]; this->array[root1] = root2; count--; } } }
实现方案
1 树结构(父指针表示法)
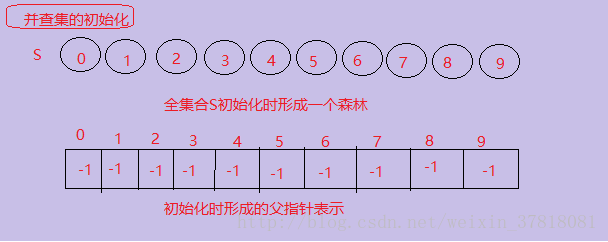
用这种实现方式,每个集合用一棵树表示,树的每一个节点代表集合的一个单元素。所有各个集合的全集合构成一个森林,并用树与森林的父指针表示法来实现。其下标代表元素名。第I个数组元素代表包含集合元素I的树节点。树的根节点的下标代表集合名,根节点的父为-1,表示集合中元素个数。
下面看一个例子:
全集合是S = {0,1,2,3,4,5,6,7,8,9},初始化每个元素自成为一个单元素子集合。(书上原图,感觉挺清晰的)
经过一段时间的计算,这些子集合并成3个集合,他们是全集合S的子集合:S1 = {0,6,7,8},S2= {1,4,9},S3 = {2,3,5}。则表示他们并查集的树形结构如下图:

上面数组中的元素值有两种含义:
(1)负数表示当前节点是树的根节点,负数的绝对值表示树中节点的个数,也即集合中元素的个数。
(2)正数表示其所属的树的根节点,由树形表示很容易理解,这也是树的父指针表示的定义。
经过上面对相关数据的组织,再回头来看并查集的3中核心操作是怎样依托于树来实现的:
(1)将root2并入到root1中,其实就可以直接把root2的数组元素(就是他的父节点)改成root1的名字(就是他所在的数组下标)。
下面的图表示了合并两个子集合的过程:

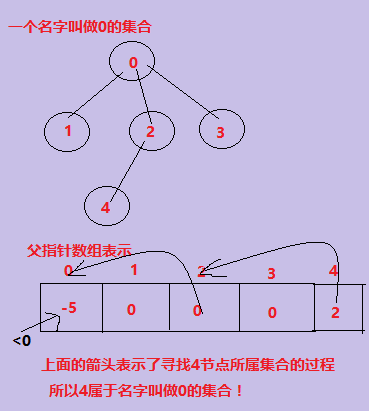
(2)查找x所属于的根节点(或者说是x所属于的集合),就可以一直找array[x],直到array[x]小于0,则证明找到了根(所在集合)。
下面的图示意了查找一个节点所属集合的过程:
(3)将整个集合初始化为单元素集合,其实就是建立树的父指针数组的过程,把数组元素全初始化为-1,也就表示了每个元素都各占一个集合。
有了上面的理论,代码也比较容易实现出来!下面给出了一个代码的实例:
/* *树结构构建并查集,其中树用父指针形式表示 */ #include <iostream> const int DefaultSize = 10; class UFSets { //集合中的各个子集合互不相交 public: UFSets(int sz = DefaultSize); //构造函数 (并查集的基本操作) ~UFSets() { delete[] parent; } //析构函数 UFSets& operator = (UFSets& R); //重载函数:集合赋值 void Union(int Root1, int Root2); //两个子集合合并 (并查集的基本操作) int Find(int x); //搜寻x所在集合 (并查集的基本操作) void WeightedUnion(int Root1, int Root2); //加权的合并算法 private: int *parent; //集合元素数组(父指针数组) int size; //集合元素的数目 }; UFSets::UFSets(int sz) { //构造函数,sz是集合元素的个数,父指针数组的范围0到sz-1 size = sz; //集合元素的个数 parent = new int[size]; //开辟父指针数组 for (int i = 0; i < size; i ++) { //初始化父指针数组 parent[i] = -1; //每个自成单元素集合 } } int UFSets::Find(int x) { //函数搜索并返回包含元素x的树的根 while (parent[x] >= 0) { x = parent[x]; } return x; } void UFSets::Union(int Root1, int Root2) { //函数求两个不相交集合的并,要求Root1与Root2是不同的,且表示了子集合的名字 parent[Root1] += parent[Root2]; //更新Root1的元素个数 parent[Root2] = Root1; //令Root1作为Root2的父节点 } void UFSets::WeightedUnion(int Root1, int Root2) { //使用节点个数探查方法求两个UFSets集合的并 int r1 = Find(Root1); //找到root1集合的根 int r2 = Find(Root2); //找到root2集合的根 if (r1 != r2) { //两个集合不属于同一树 int temp = parent[r1] + parent[r2]; //计算总节点数 if (parent[r2] < parent[r1]) { //注意比较的是负数,越小元素越多,此处是r2元素多 parent[r1] = r2; //r1作为r2的孩子 parent[r2] = temp; //更新r2的节点个数 } else { parent[r2] = r1; //... parent[r1] = temp; //... } } }
代码的注释比较详尽,我就不在赘言。但是有一个注意点我已经写在了下面!
当前并查集的改进!
的确,有一个极端的状况使得上面的树实现的并查集性能低下!问题原因在于,这里没有规定子集合并的顺序,更确切的说是子集一直在向同一个方向依附:
下面的图片展示了当Union(0,1),Union(1,2),Union(2,3),Union(3,4)执行完后的树的形状。

在这种极端情况下他编变成了一个单链表(退化的树),这样的话,用Find函数查找完所有的节点所归属的集合将会开销的时间复杂度为:O(n^2)。