Codeforces Round #467 (Div. 2)

题目链接：http://codeforces.com/contest/937

B. Vile Grasshoppers

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

The weather is fine today and hence it's high time to climb the nearby pine and enjoy the landscape.

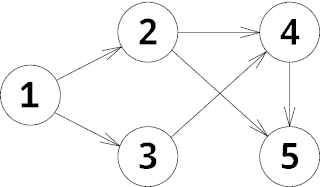
The pine's trunk includes several branches, located one above another and numbered from 2 to y. Some of them (more precise, from 2 to p) are occupied by tiny vile grasshoppers which you're at war with. These grasshoppers are known for their awesome jumping skills: the grasshopper at branch x can jump to branches .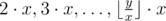

Keeping this in mind, you wisely decided to choose such a branch that none of the grasshoppers could interrupt you. At the same time you wanna settle as high as possible since the view from up there is simply breathtaking.

In other words, your goal is to find the highest branch that cannot be reached by any of the grasshoppers or report that it's impossible.

Input

The only line contains two integers p and y (2 ≤ p ≤ y ≤ 109).

Output

Output the number of the highest suitable branch. If there are none, print -1 instead.

Examples

input

Copy

3 6

output

Copy

5

input

Copy

3 4

output

Copy

-1

Note

In the first sample case grasshopper from branch 2 reaches branches 2, 4 and 6 while branch 3 is initially settled by another grasshopper. Therefore the answer is 5.

It immediately follows that there are no valid branches in second sample case.

题解：

问：在[2,y]范围内，不能被[2,p]整除的最大整数，其中p<=y, y<=1e9。

1.可知，小于y且大于p的最大素数即为答案，而两个素数间的间隔不会太大（好像是300左右），所以可以直接从y递减枚举答案ans，看是否不能被[2,p]整除。

2.由于p的范围也可达到1e9，如果直接判断ans能否被[2,p]整除，也必定会超时，所以需要优化。根据以往的经验，求一个数的因子ai，我们只需要枚举到sqrt(n)，而与之对应的另一个因子aj为n/ai。那么对于此题，我们也可以这样优化：判断ans能否被[2,min(p,sqrt(y))]中的整除。这样整体复杂度就达到 300*sqrt(1e9)了。

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <sstream>
#include <algorithm>
using namespace std;
typedef long long LL;
const double eps = 1e-8;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 2e5+10;

int a[MAXN];
int main()
{
    int y, p;
    while(scanf("%d%d",&p,&y)!=EOF)
    {
        bool flag = 0;
        int ans = 0;
        for(; y>p; y--)
        {
            bool f = true;
            int m = sqrt(y); m++;
            int maxx = min(m,p);
            for(int i = 2; i<=maxx; i++)
                if(y%i==0)
                {
                    f = false;
                    break;
                }

            if(f)
            {
                printf("%d
", y);
                flag = true;
                break;
            }
        }

        if(!flag) puts("-1");
    }
}

C. Save Energy!

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Julia is going to cook a chicken in the kitchen of her dormitory. To save energy, the stove in the kitchen automatically turns off after kminutes after turning on.

During cooking, Julia goes to the kitchen every d minutes and turns on the stove if it is turned off. While the cooker is turned off, it stays warm. The stove switches on and off instantly.

It is known that the chicken needs t minutes to be cooked on the stove, if it is turned on, and 2t minutes, if it is turned off. You need to find out, how much time will Julia have to cook the chicken, if it is considered that the chicken is cooked evenly, with constant speed when the stove is turned on and at a constant speed when it is turned off.

Input

The single line contains three integers k, d and t (1 ≤ k, d, t ≤ 1018).

Output

Print a single number, the total time of cooking in minutes. The relative or absolute error must not exceed 10 - 9.

Namely, let's assume that your answer is x and the answer of the jury is y. The checker program will consider your answer correct if .

Examples

input

Copy

3 2 6

output

Copy

6.5

input

Copy

4 2 20

output

Copy

20.0

Note

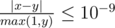In the first example, the chicken will be cooked for 3 minutes on the turned on stove, after this it will be cooked for . Then the chicken will be cooked for one minute on a turned off stove, it will be cooked for 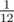. Thus, after four minutes the chicken will be cooked for . Before the fifth minute Julia will turn on the stove and after 2.5 minutes the chicken will be ready .

In the second example, when the stove is turned off, Julia will immediately turn it on, so the stove will always be turned on and the chicken will be cooked in 20 minutes.

题解：

可分为三种情况：

1.d能整除k，即在火炉熄灭的一瞬间，人刚好去检查，并把火炉重新打开，所以时间为t；

2.k<d，那么每一次火炉熄灭后，都要等上(d-k)个时间，再被重新打开，所以是一个循环。

3.当k>d时，即在火炉熄灭前，人已经检查了若干次，但这些检查都是无用的，真正有用的是第i次，使得i*d>k。在前k个时间内，火炉一直开着，过了k之后，火炉就熄灭了，知道i*d时刻，火炉才被重新启动。因此也是一个循环。

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <sstream>
#include <algorithm>
using namespace std;
typedef long long LL;
const double eps = 1e-8;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 2e5+10;


int main()
{
    LL k, d, t;
    scanf("%lld%lld%lld",&k,&d,&t);
    double time = 0, c = 1.0/t, w = 0.5/t;  //单位时间
    if(k%d==0)
        time = 1.0*t;
    else if(k<d)
    {
        double ui = k*c+(d-k)*w;
        LL cnt = (LL)(1.0/ui);
        time += cnt*d;
        double left = 1.0-cnt*ui;
        if(left<=c*k) time += left/c;
        else time += k+(left-c*k)/w;
    }
    else
    {
        LL gap = (k/d+1)*d-k;

        double ui = k*c+gap*w;
        LL cnt = (LL)(1.0/ui);
        time += cnt*(k+gap);
        double left = 1.0-cnt*ui;
        if(left<=c*k) time += left/c;
        else time += k+(left-c*k)/w;
    }
    printf("%f
", time);
}

D. Sleepy Game

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Petya and Vasya arranged a game. The game runs by the following rules. Players have a directed graph consisting of n vertices and medges. One of the vertices contains a chip. Initially the chip is located at vertex s. Players take turns moving the chip along some edge of the graph. Petya goes first. Player who can't move the chip loses. If the game lasts for 106 turns the draw is announced.

Vasya was performing big laboratory work in "Spelling and parts of speech" at night before the game, so he fell asleep at the very beginning of the game. Petya decided to take the advantage of this situation and make both Petya's and Vasya's moves.

Your task is to help Petya find out if he can win the game or at least draw a tie.

Input

The first line of input contain two integers n and m — the number of vertices and the number of edges in the graph (2 ≤ n ≤ 105, 0 ≤ m ≤ 2·105).

The next n lines contain the information about edges of the graph. i-th line (1 ≤ i ≤ n) contains nonnegative integer ci — number of vertices such that there is an edge from i to these vertices and ci distinct integers ai, j — indices of these vertices (1 ≤ ai, j ≤ n, ai, j ≠ i).

It is guaranteed that the total sum of ci equals to m.

The next line contains index of vertex s — the initial position of the chip (1 ≤ s ≤ n).

Output

If Petya can win print «Win» in the first line. In the next line print numbers v1, v2, ..., vk (1 ≤ k ≤ 106) — the sequence of vertices Petya should visit for the winning. Vertex v1 should coincide with s. For i = 1... k - 1 there should be an edge from vi to vi + 1 in the graph. There must be no possible move from vertex vk. The sequence should be such that Petya wins the game.

If Petya can't win but can draw a tie, print «Draw» in the only line. Otherwise print «Lose».

Examples

input

Copy

5 6
2 2 3
2 4 5
1 4
1 5
0
1

output

Copy

Win
1 2 4 5 

input

Copy

3 2
1 3
1 1
0
2

output

Copy

Lose

input

Copy

2 2
1 2
1 1
1

output

Copy

Draw

Note

In the first example the graph is the following:

Initially the chip is located at vertex 1. In the first move Petya moves the chip to vertex 2, after that he moves it to vertex 4 for Vasya. After that he moves to vertex 5. Now it is Vasya's turn and there is no possible move, so Petya wins.

In the second example the graph is the following:

Initially the chip is located at vertex 2. The only possible Petya's move is to go to vertex 1. After that he has to go to 3 for Vasya. Now it's Petya's turn but he has no possible move, so Petya loses.

In the third example the graph is the following:

Petya can't win, but he can move along the cycle, so the players will draw a tie.

题意：

给出一副有向图（可能含有环、自环），问以s为起点，是否存在一条结点数为偶数的路径，且末尾结点没有后继结点，如果有，输出“win”并且输入路径；否则，再寻找是否存在一条以s为起点，形成回路的路径（s可以不在回路内），如果有，则输出“draw”否则输出“lose”。

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <sstream>
#include <algorithm>
using namespace std;
typedef long long LL;
const double eps = 1e-8;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 2e5+10;

int viss[MAXN], vis[MAXN][2];
vector<int>son[MAXN];

int ans[MAXN], tt;
int dfs(int u, int s)
{
    if(vis[u][s&1]) return false;   //此种方式走过了，即证明行不通（如果行得通，那在第一次走的时候就直接返回true了）
    ans[s] = u; //先把答案存起来
    vis[u][s&1] = 1;
    if((s&1)==0&&son[u].size()==0) return tt=s, true;   //找到偶数长度的路径，且末尾结点没有后继结点，则能赢

    for(int i = 0; i<son[u].size(); i++)
    {
        int v = son[u][i];
        if(!vis[v][(s+1)&1]&&dfs(v,s+1))
            return true;
    }
    return false;
}

bool check(int u)
{
    viss[u] = 1;    //标记1：孙子结点没有被遍历完全
    int sz = son[u].size();
    for(int i = 0; i<sz; i++)
    {
        int v = son[u][i];
        if(!viss[v]&& check(v)) return true;
        else if(viss[v]==1) return true;    //如果找到孙子结点没有被遍历完全的结点，即证明是该节点的祖先，形成环。
    }
    viss[u] = 2;    //标记2：孙子结点遍历完全
    return false;
}

int main()
{
    int n,m,s;
    while(scanf("%d%d",&n,&m)!=EOF)
    {
        for(int i = 1; i<=n; i++)
        {
            son[i].clear();
            int c, v;
            scanf("%d",&c);
            while(c--)
            {
                scanf("%d",&v);
                son[i].push_back(v);
            }
        }
        scanf("%d",&s);

        tt = 0;
        memset(vis, 0, sizeof(vis));
        if(dfs(s,1))
        {
            puts("Win");
            for(int i = 1; i<=tt; i++)
                printf("%d ", ans[i]);
            puts("");
        }
        else
        {
            memset(vis, 0, sizeof(vis));
            printf("%s
", check(s)?"Draw":"Lose");
        }
    }
}

E. Lock Puzzle

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Welcome to another task about breaking the code lock! Explorers Whitfield and Martin came across an unusual safe, inside of which, according to rumors, there are untold riches, among which one can find the solution of the problem of discrete logarithm!

Of course, there is a code lock is installed on the safe. The lock has a screen that displays a string of n lowercase Latin letters. Initially, the screen displays string s. Whitfield and Martin found out that the safe will open when string t will be displayed on the screen.

The string on the screen can be changed using the operation «shift x». In order to apply this operation, explorers choose an integer xfrom 0 to n inclusive. After that, the current string p = αβ changes to βRα, where the length of β is x, and the length of α is n - x. In other words, the suffix of the length x of string p is reversed and moved to the beginning of the string. For example, after the operation «shift4» the string «abcacb» will be changed with string «bcacab », since α = ab, β = cacb, βR = bcac.

Explorers are afraid that if they apply too many operations «shift», the lock will be locked forever. They ask you to find a way to get the string t on the screen, using no more than 6100 operations.

Input

The first line contains an integer n, the length of the strings s and t (1 ≤ n ≤ 2 000).

After that, there are two strings s and t, consisting of n lowercase Latin letters each.

Output

If it is impossible to get string t from string s using no more than 6100 operations «shift», print a single number  - 1.

Otherwise, in the first line output the number of operations k (0 ≤ k ≤ 6100). In the next line output k numbers xi corresponding to the operations «shift xi» (0 ≤ xi ≤ n) in the order in which they should be applied.

Examples

input

Copy

6
abacbb
babcba

output

Copy

4
6 3 2 3

input

Copy

3
aba
bba

output

Copy

-1

In the first example, after applying the operations, the string on the screen will change as follows:

1. abacbb  bbcaba
2. bbcaba  ababbc
3. ababbc  cbabab
4. cbabab  babcba

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <sstream>
#include <algorithm>
using namespace std;
typedef long long LL;
const double eps = 1e-8;
const int INF = 2e9;
const LL LNF = 9e18;
const int MOD = 1e9+7;
const int MAXN = 2e5+10;

int n;
char s[MAXN], t[MAXN];
int ans[MAXN], tot;
void turn(int pos)
{
    char tmp = s[pos];
    reverse(s+pos+1,s+n+1);
    for(int i = pos-1; i>=1; i--) s[i+1] = s[i];
    s[1] = tmp;
    ans[++tot] = n; ans[++tot] = pos-1; ans[++tot] = 1;
}

int main()
{
    while(scanf("%d",&n)!=EOF)
    {

        bool flag = true;
        tot = 0;
        scanf("%s%s",s+1,t+1);
        for(int i = 1; i<=n; i++)
        {
            int pos = i;
            while(pos<=n&& s[pos]!=t[n-i+1]) pos++;
            if(pos>n)
            {
                flag = false;
                break;
            }
            turn(pos);
        }

        if(flag)
        {
            printf("%d
", tot);
            for(int i = 1; i<=tot; i++)
                printf("%d ", ans[i]);
            puts("");
        }
        else puts("-1");
    }
}