后缀数组小结

一.必备学习资料

《后缀数组——处理字符串的有力工具》

二. 模板及其注解：

//Rank[0~n-1]为有效值， Rank[n]必定为0是无效值。
//sa[1~n]为有效值，sa[0]必定为n是无效值。
//height[2~n]为有效值；height[1]为0。
bool cmp(int *r, int a, int b, int l)
{
    return r[a]==r[b] && r[a+l]==r[b+l];
}

int r[MAXN], sa[MAXN], Rank[MAXN], height[MAXN];
int t1[MAXN], t2[MAXN], c[MAXN];
void DA(int str[], int sa[], int Rank[], int height[], int n, int m)
{
    n++;    // 加多一位是为了在第一名之前插多一名，且为'',即字典序最小的，以便处理边界问题。
    int i, j, p, *x = t1, *y = t2;
    for(i = 0; i<m; i++) c[i] = 0;  //初始化每个“桶”
    for(i = 0; i<n; i++) c[x[i] = str[i]]++; //把每个数入桶
    for(i = 1; i<m; i++) c[i] += c[i-1];    // 求前缀和， 以便求出排名
    for(i = n-1; i>=0; i--) sa[--c[x[i]]] = i;  /*求出每个数的排名。这里从0开始枚举应该没问题， 
                                                  而下面那句必须从n-1来时枚举，详情看下面注释*/
    for(j = 1; j<=n; j <<= 1)
    {
        //x相当于Rank， y相当于sa
        //对第二关键字进行排序（借助上一次的第一关键字）：
        p = 0;
        for(i = n-j; i<n; i++) y[p++] = i;  //没有第二关键字的，第二关键字设为最小。这里从n-1开始枚举应该没问题。
        for(i = 0; i<n; i++) if(sa[i]>=j) y[p++] = sa[i]-j; //枚举sa数组，sa[i]-j的第二关键字为sa[i]
        //对第二关键字进行排序
        for(i = 0; i<m; i++) c[i] = 0;
        for(i = 0; i<n; i++) c[x[y[i]]]++;
        for(i = 1; i<m; i++) c[i] += c[i-1];
        for(i = n-1; i>=0; i--) sa[--c[x[y[i]]]] = y[i]; /*因为y的顺序是按照第二关键字的顺序来排的
                                                           第二关键字靠后的，在同一个第一关键字桶中排名越靠后*/

        //重新求x（即Rank），因为此时y没有作用，所以把x复制到y上，然后再根据y对x重新求值。
        swap(x, y);
        p = 1; x[sa[0]] = 0;
        for(i = 1; i<n; i++)
            x[sa[i]] = cmp(y, sa[i-1], sa[i], j)?p-1:p++;
        if(p>=n) break; //关键字会越来越多，当大于等于n个时，即表明所有位置的排名都已明确，则排序结束。
        m = p;
    }

    int k = 0;
    n--;
    for(i = 0; i<=n; i++) Rank[sa[i]] = i;  //注:sa[0]必定为n， 因而避免了sa[Rank[i]-1]溢出。
    for(i = 0; i<n; i++)  //sa[0]必定为n， 即Rank[n]必定为0，所以只枚举到n-1，避免了sa[Rank[i]-1]溢出。
    {
        /*
            i与sa[Rank[i]-1]的最长前缀为height[Rank[i]]],
            那么i与sa[Rank[i]-1]都去掉第一个字符，就得到 i+1与sa[Rank[i]-1]+1，
            而i+1与sa[Rank[i]-1]+1的最长前缀显然为height[Rank[i]]-1.
            所以 height[Rank[i+1]] >= height[Rank[i]]-1。因而可以根据这个性质加快速度。
        */
        if(k) k--;
        j = sa[Rank[i]-1];
        while(str[i+k]==str[j+k]) k++;
        height[Rank[i]] = k;
    }
}

看排序过程有助于理解：https://zhuanlan.zhihu.com/p/21283102?refer=Vector

三. 题目分类（依照论文）

1. 单个字符串的相关问题

1.1 重复子串

POJ1743 Musical Theme（ 重复出现且不重叠的最长子串）

POJ3261 Milk Patterns （出现k次且可重叠的最长子串）

SPOJ - REPEATS（重复次数最多的连续重复子串）

POJ3693 Maximum repetition substring （重复次数最多的连续重复子串）

1.2 子串的个数

SPOJ - SUBST1 New Distinct Substrings 

1.3  回文子串

URAL - 1297 Palindrome（最长回文子串）

UVA - 11475 Extend to Palindrome （往后添加字符使其成为回文串）

1.4 连续重复子串

POJ2406 Power Strings

1.5 其他

POJ3581 Sequence

2. 两个字符串的相关问题

2.1 最长公共子串

POJ2774 Long Long Message

POJ1226 Substrings （可存在于逆串中）

2.2 公共子串个数

POJ3415 Common Substrings

3. 多个字符串的相关问题

POJ3294 Life Forms（不小于k个字符串中的最长子串）

SPOJ - PHRASES Relevant Phrases of Annihilation（每个字符串中至少出现两次且不重叠的最长子串）

POJ3450 Corporate Identity（每个字符串中出现的最长子串）

四 理解

1.sa[]数组：sa[i] = j， 排名为第i的是suffix[j]。

假设字符串长度为n，下标从1开始，后缀排名从1开始。那么按照排名从前到后把后缀排成一列，如图：

 

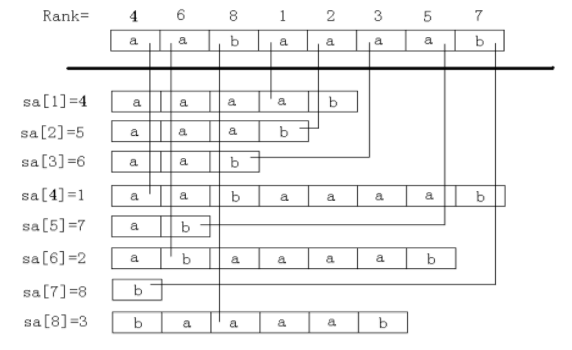
2.rank[]数组：rank[i] = j，suffix[i]排名第j。

3.height[]数组：suffix[sa[i]] 与 suffix[sa[i-1]]（即suffix[sa[i]]与它前一名）的最长公共前缀。

4.三者之间的关系

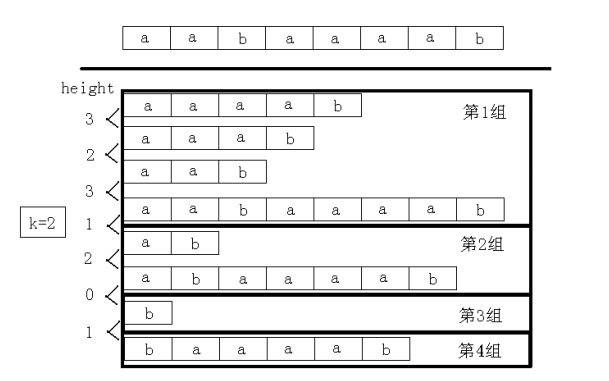
1） 求sa[i]与sa[j]的最长公共前缀lcp， 则 lcp =（height[k]）， i+1<=k<=j （假设i<j）。

2） 求suffix[i]与suffix[j]的最长公共前缀lcp， 则 lcp = min（height[k]）， min(rank[i], rank[j])+1<=k<= max(rank[i], rank[j]) 。常使用RMQ进行预处理。

3）当要求把后缀分成若干组，且每一组的最长公共前缀不小于k，则每一组在sa[]数组，即排名内是连续的。话句话说：长度k把排名分成了若干组，且每一组的最长公共前缀不小于k，如下图：