URAL1099 Work Scheduling —— 一般图匹配带花树

题目链接：https://vjudge.net/problem/URAL-1099

1099. Work Scheduling

Time limit: 0.5 second
Memory limit: 64 MB

There is a certain amount of night guards that are available to protect the local junkyard from possible junk robberies. These guards need to be scheduled in pairs so that each pair guards in a different night. The junkyard CEO ordered you to write a program which given the guards characteristics determines the maximum amount of scheduled guards (the rest will be fired). Please note that each guard can be scheduled with only one of his colleagues and no guard can work alone.

Input

The first line of the input contains one number N ≤ 222 which is a number of night guards. Unlimited number of lines consisting of unordered pairs (i, j) follow, each such pair means that guard #i and guard #j can work together, because it is possible to find uniforms that suit both of them (The junkyard uses different parts of uniforms for different guards i.e. helmets, pants, jackets. It is impossible to put small helmet on a guard with a big head or big shoes on guard with small feet). The input ends with Eof.

Output

You should output one possible optimal assignment. On the first line of the output write the even number C, the amount of scheduled guards. Then output C/2 lines, each containing 2 integers (i, j) that denote that i and j will work together.

Sample

input	output
3 1 2 2 3 1 3	2 1 2

题解：

一般图匹配带花树的模板题。还是看不太懂，以后有时间再看看。

有关怎么找到奇环：

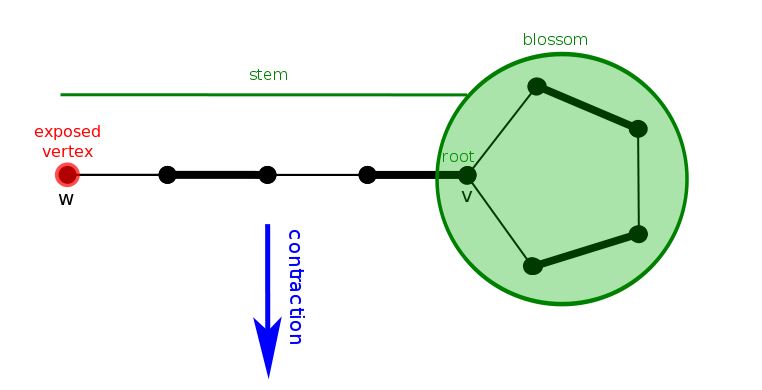
其中可以把最右边两个点看成是找到奇环时的两个点，其中root为他们的LCA。

疑问1：什么要把花上的边的方向取反？

疑问2：为什么在找奇环时要特判 v==start ？

代码如下：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <string>
#include <vector>
#include <map>
#include <set>
#include <queue>
#include <sstream>
#include <algorithm>
using namespace std;
const int INF = 2e9;
const int MOD = 1e9+7;
const int MAXM = 20+10;
const int MAXN = 2e3+10;

int N;
bool graph[MAXN][MAXN];
int match[MAXN];
bool inque[MAXN], inpath[MAXN], inblos[MAXN];
queue<int>q;
int start, finish;
int newbase, fa[MAXN], base[MAXN];

int FindCommonAncester(int u, int v)   //仅仅是找LCA，并不修改任何值
{
    memset(inpath, false, sizeof(inpath));
    while(true)
    {
        u = base[u];
        inpath[u] = true;
        if(u==start) break;
        u = fa[match[u]];
    }
    while(true)
    {
        v = base[v];
        if(inpath[v]) break;
        v = fa[match[v]];
    }
    return v;
}

void ResetTrace(int u)  //把fa的方向取反
{
    int v;
    while(base[u]!=newbase) //匹配边、非匹配边交替出现
    {
        v = match[u];   //u--match[u]匹配边
        inblos[base[u]] = inblos[base[v]] = true;
        u = fa[v];      //v--fa[v]非匹配边
        if(base[u]!=newbase) fa[u] = v;
    }
}

void BloosomContract(int u, int v)
{
    newbase = FindCommonAncester(u, v);
    memset(inblos, false, sizeof(inblos));
    ResetTrace(u);   //把u到LCA上的边取反
    ResetTrace(v);   //把v到LCA上的边取反
    if(base[u]!=newbase) fa[u] = v; //看不懂
    if(base[v]!=newbase) fa[v] = u;

    for(int tu = 1; tu<=N; tu++)
    if(inblos[base[tu]])
    {
        base[tu] = newbase;     //设置它属于的集合
        if(!inque[tu]) q.push(tu);  //在花中的点加入队列，因为与花中点相连的点还可以找增广路
    }
}

void FindAugmentingPath()
{
    memset(inque, false, sizeof(inque));
    memset(fa, 0, sizeof(fa));
    for(int i = 1; i<=N; i++)
        base[i] = i;
    while(!q.empty()) q.pop();
    q.push(start);
    finish = 0;

    while(!q.empty())
    {
        int u = q.front(); q.pop();

        for(int v = 1; v<=N; v++)  //fa[u]--u是匹配边, u--v是未匹配边。
        if(graph[u][v] && base[u]!=base[v] && match[u]!=v )
        {
            //为什么要特判 v==start ？
            if( (v==start) || (match[v]>0 && fa[match[v]]>0))   //找到奇环。
                BloosomContract(u, v);
            else if(fa[v]==0)   //v点在这次找增广路时没有被访问
            {
                fa[v] = u;
                if(match[v]>0)  //如果已经匹配了，则加入他的匹配点，继续找增广路。
                    q.push(match[v]);
                else    //如果没有匹配，则找到了增广路。
                {
                    finish = v;
                    return;
                }
            }
        }
    }
}

void AugmentPath()
{
    int u, v, w;
    u = finish;
    while(u>0)  //沿着增广路往回走，把匹配边和非匹配边取反
    {
        v = fa[u];
        w = match[v];
        match[v] = u;
        match[u] = v;
        u = w;
    }
}

void Edmonds()
{
    memset(match, 0, sizeof(match));
    for(int u = 1; u<=N; u++)
    if(match[u]==0)
    {
        start = u;
        FindAugmentingPath();
        if(finish>0) AugmentPath();
    }
}

int main()
{
    scanf("%d", &N);
    memset(graph, false, sizeof(graph));
    int u, v;
    while(scanf("%d%d", &u, &v)!=EOF)
        graph[u][v] = graph[v][u] = true;

    Edmonds();
    int sum = 0;
    for(int u = 1; u<=N; u++)
        if(match[u]>0) sum++;
    printf("%d
", sum);
    for(int u = 1; u<=N; u++)
        if(u<match[u])
            printf("%d %d
", u, match[u]);

    return 0;
}