1.BP neural network optimized by PSO algorithm on Ammunition storage reliability prediction 文献简介
文献来源:https://ieeexplore.ieee.org/document/8242856
文献级别:EI检索
摘要:Storage reliability of the ammunition dominates the efforts in achieving the mission reliability goal. Prediction of storage reliability is important in practice to monitor the ammunition quality. In this paper we provided an integrated method where particle swarm optimization (PSO) algorithm is applied to adjust and optimize the BP neural network global parameters (weights and thresholds). The experiment results show that PSO-BP algorithm can achieve the convergence rate and increase the prediction accuracy of storage reliability.
弹药的贮存可靠性是实现任务可靠性目标的关键。在弹药质量监测中,贮存可靠性的预测具有重要的现实意义。本文提出了一种应用粒子群优化算法对BP神经网络全局参数(权重和阈值)进行调整和优化的综合方法。实验结果表明,PSO-BP算法能够达到收敛速度,提高存储可靠性的预测精度。
关键词:BP neural network; prediction; Storage reliability (BP神经网络,预测,贮存可靠性)
主要内容和思想:作者首先说明了弹药贮存可靠性是弹药后勤保障技术的核心,也是衡量国家弹药技术水平一项重要指标。由此提出论文中弹药贮存可靠性的预测具有重大研究意义。接着介绍了一些常用的方法(文献调研,总结其他人的工作),然后,引出了自己对该问题的解决方法:即是提出了一种基于粒子群优化的PSO-BP神经网络算法,利用粒子群优化方法对神经网络的权值和阈值进行优化,使得PSO-BP算法的预测性能优于BP神经网络。随后简要介绍了PSO算法和BP神经网络,详细介绍了PSO-BP算法,并且阐述了实验过程和结果,最后,作出了总结性评论。
2.PSO算法和BP神经网络
2.1Particle Swarm Optimization Algorithm (PSO)算法
埃伯哈特和肯尼迪[10]提出的粒子群优化算法是一种进化计算技术,受鸟类群的捕食行为的启发,用于求解优化问题。粒子群算法可以描述如下:假设在D维搜索空间中存在一个大小为N的粒子群。
Xi=(xi1,…,xiD) i=1,…,N 表示粒子 i 的位置
Vi=(vi1,…,viD) i=1,…,N 表示粒子 i 的速度
随机生成一组具有位置和速度的粒子,计算每个粒子的适应度fitness(i),每个粒子都可以通过全局搜索和局部搜索之间的迭代操作来更新和调整自己的搜索方向。令pbest为每个粒子迄今为止搜索到的最优位置(个体极值),gbest为整个个粒子群迄今为止搜索到的最优位置(全局极值)。通过以下两个公式更新粒子的速度和位置:
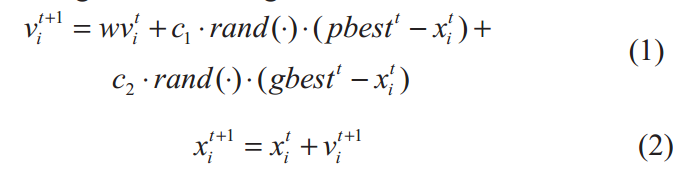
式中, vit是迭代次数为t时粒子i的速度,xit是迭代次数为t时粒子i的位置。粒子的速度通常限制在区间[-vmax, vmax]内。c1和c2是学习因子;rand()是统一来自[0,1]的随机数。PBestt和GBestt分别是迭代次数为t时所有粒子的个体最佳位置和全局最佳位置。变量w是迭代次数为t时的惯性权重,其定义如下:

其中wmax和wmin分别是惯性重量的最大值和最小值,tmax是最大迭代次数。一般来说,wmax=0.9,wmin=0.4。
2.2BP神经网络
BP神经网络的结构是三层网络:输入层、隐藏层和输出层。在本文中,我们选择八个节点作为输入层。输出层中只有一个节点,即是是弹药储存可靠性预测值。由于隐层影响网络的鲁棒性,采用Hecht-Nelson方法[11]确定隐层的节点数。隐藏层h的节点数范围由三种公式确定:2n+1、√(n+m)+α和(m+n)/2,其中n是输入层的节点数,m是输出层的节点数,α是[1,10]中的常数。
3.PSO-BP神经网络预测方法
粒子群优化算法优化的BP神经网络即为是PSO-BP算法。文中提出的PSO-BP神经网络可用于弹药贮存可靠性的预测。PSO-BP算法优化了粒子群算法训练神经元的权值和偏差。PSO-BP算法的总体工作流程如图1所示

该算法的具体步骤描述如下:
step1:将训练数据集和测试数据集规范化为[0,1]之间。在标准化之后,为网络构建训练和测试样本。设置神经网络的输入层节点数、隐藏层节点数、输出层节点数。
step2:随机产生初始的一组种群规模为N 的粒子及其位置和速度。设置参数,例如迭代次数、惯性权重和学习因子。计算推断的网络输出向量和权重矩阵变化。
step3:计算每次迭代时每个粒子的适应度值,并记录全局极值和个体极值。更新每个粒子的位置和速度。将个体极值与全局极值进行比较。如果粒子个体极值优于全局最佳值,则更新全局最佳值。
step4:使用当前gbest值更新每个神经元的权值和偏值。选择MSE函数作为性能函数,用均方误差表示![]() 其中yid和yi分别是网络输出的期望值和实际值。
其中yid和yi分别是网络输出的期望值和实际值。
4.仿真实验的实现
4.1数据集
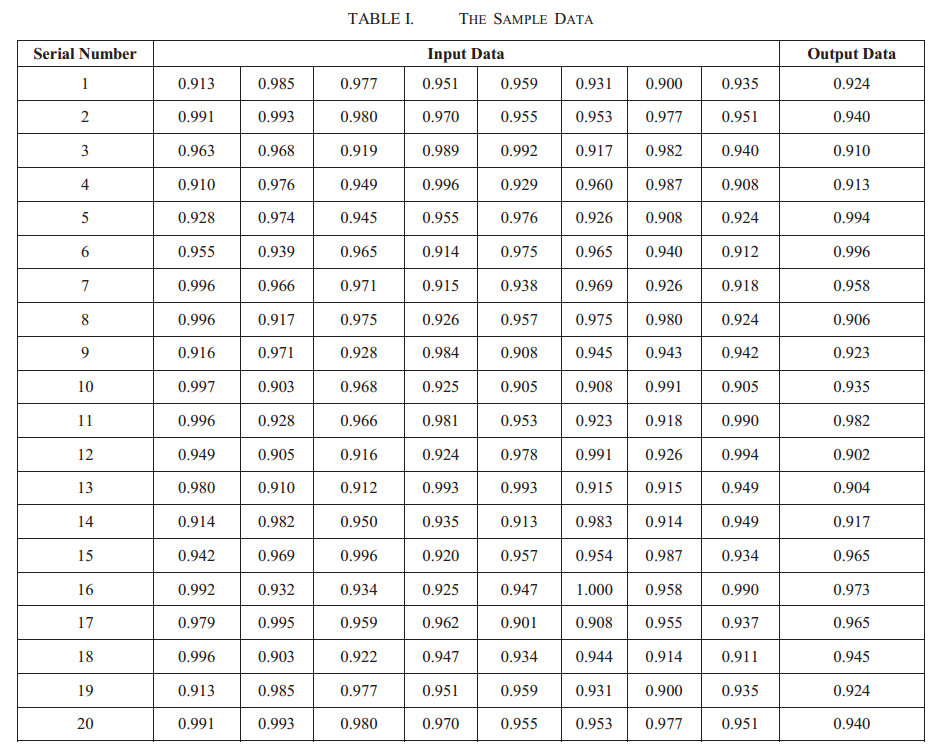
论文中选取了20组弹药数据进行实验,如下图所示,其中前12组为训练集,后8组为测试集,每一组数组的前8列为输入,最后一列为输出,该数据是已经经过归一化处理后的数据。
4.2BP神经网络和PSO的参数设置
(1)BP神经网络的参数设置:
输入层节点:8
隐藏层节点:11(通过训练3-17的发现11是最优的)
输出层节点:1
最大训练次数:10000
学习率:0.5
精度:0.001
激活函数:tansig和logsig
训练函数:分别采用了traingdm和traingda进行对比
其中隐藏层是经过分别选取3-17的数作为隐藏层节点,然后训练网络,发现选择11的效果最好,如下图:

(2)PSO的参数设置:
粒子数目:30
维度:D=(n+m)*h+h+m n:输入层节点数,m:输出层节点数,h:隐藏层节点数
最大速度:1
学习因子:c1=c2=2
最大迭代次数:1000
惯性权重:wmax =0.9 , wmin =0.4.
4.3实验仿真结果

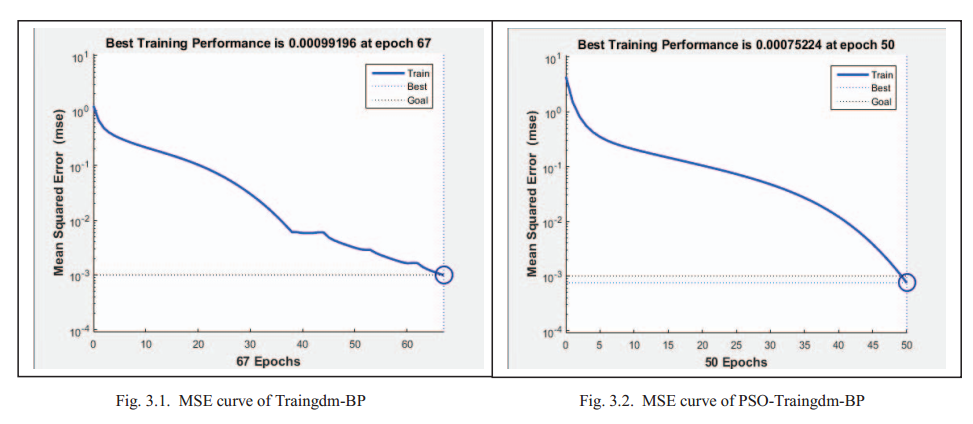
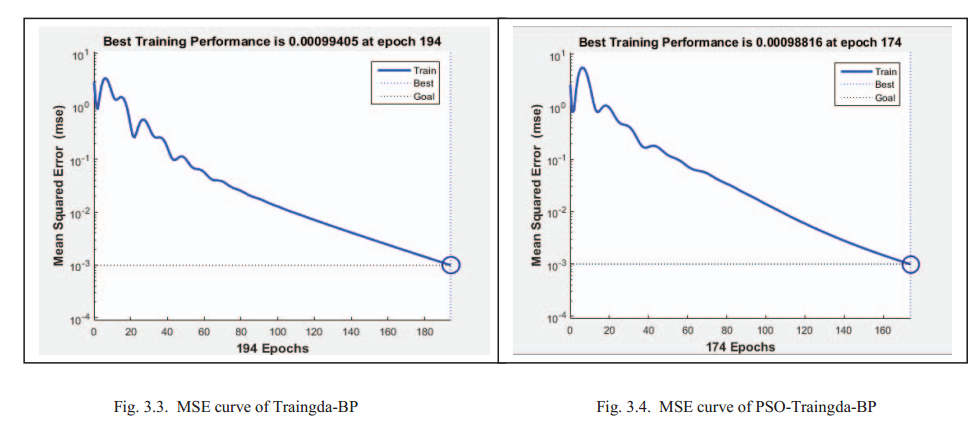
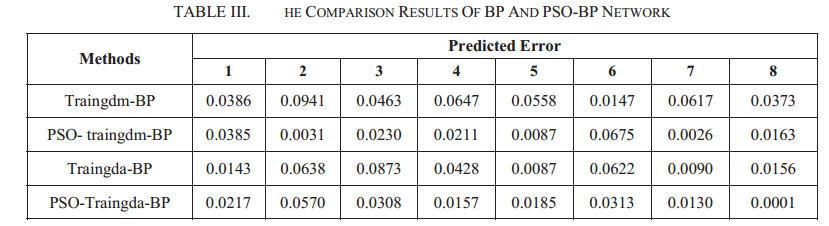

BP神经网络和PSOBP神经网络的实验结果如表3所示。可以看出,PSO-BP方法的性能优于BP方法。图2.1和图2.2表明,PSO-BP方法的预测精度大于98%。从图3.1—图3.4可以看出,当训练要求精度达到0.01时,两种算法都能满足预测误差的精度。PSO-BP方法的迭代次数小于BP方法的迭代次数。这意味着算法是收敛的。MSE曲线进一步说明了PSO-BP方法的稳定性优于BP方法。最后的图表明,PSO-BP方法的预测误差小于BP方法。结果表明,与常规BP算法相比,PSO-BP算法在最优参数搜索中具有更好的性能。PSO-BP方法的预测性能更适合于弹药储存的可靠性。
5.总结
文章运用了粒子群算法来优化BP神经网络中的权值和阈值,以此来提高弹药存储预测性能,而且预测精度也确实得到了提高,但由于数据集共有20组(也许是弹药数据的特殊性),还是觉得结果可能难以让人信服,但思路确实还是有用的,准备后面把该文的实验复现一下,或者用其他数据量比较大的预测数据,看下结果,再看一下有哪些还能值得改进的地方。