《数值分析引论》-易大义,陈道琦
P387 第一题(1)(2)
1.二分法(对分法或分半法)
1 import math 2 import numpy as np 3 import matplotlib.pyplot as plt 4 5 a=0.3 6 b=0.4 7 h=b-a 8 p=1e-4 9 x = np.arange(-0.3, 0.4, 0.0001)#可以自动生成x轴坐标,最小间隔为0.0001 10 y=x**4-3*x+1 11 plt.style.use('ggplot')#使用‘ggplot风格美化图表’ 12 plt.xlabel(u"x") 13 plt.title(u'Dichotomy for roots') 14 plt.plot(x,y,'r',linewidth=2) 15 #计算迭代次数N 16 N=math.ceil((math.log((b-a)/p)/math.log(2)))#向上取整 17 A=[0]*(N+1) 18 B=[0]*(N+1) 19 X=[0]*(N+1)#保存中点 20 F=[0]*(N+1)#保存中点的函数值 21 FA=[0]*(N+1) 22 x1=[0]*(N+1) 23 A[0]=a 24 B[0]=b 25 for i in range(N): 26 X[i]=(A[i]+B[i])/2 27 F[i]=X[i]**4-3*X[i]+1 28 FA[i]=A[i]**4-3*A[i]+1 29 if F[i]==0: 30 x1=X[i] 31 elif F[i]*FA[i]>0: 32 A[i+1]=X[i] 33 B[i+1]=B[i] 34 elif F[i]*FA[i]<0: 35 A[i+1]=A[i] 36 B[i+1]=X[i] 37 #print(A[i],B[i],F[i],FA[i]) 38 print('使用二分法迭代%d次后的根为%f'%(N,X[-2])) 39 print('近似解序列为:',X[:-1])

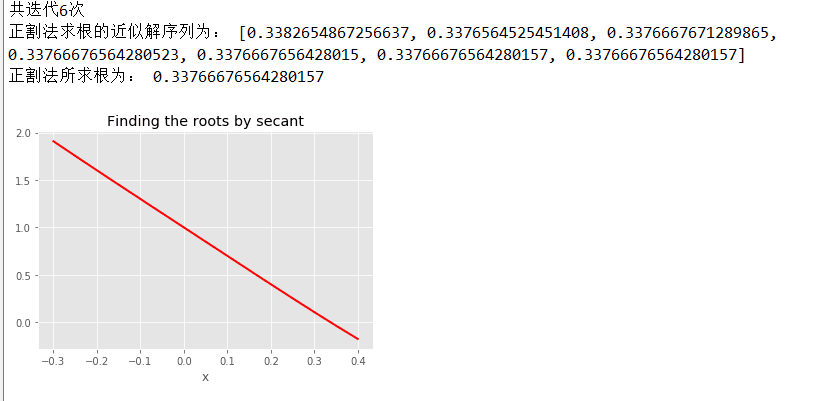
2.正割法
1 import numpy as np 2 import matplotlib.pyplot as plt 3 4 a=0.3 5 b=0.4 6 x=[0]*1000 7 X=[] 8 x1 = np.arange(-0.3, 0.4, 0.0001)#可以自动生成x轴坐标,最小间隔为0.0001 9 y=x1**4-3*x1+1 10 plt.style.use('ggplot')#使用‘ggplot风格美化图表’ 11 plt.xlabel(u"x") 12 plt.title(u'Finding the roots by secant') 13 plt.plot(x1,y,'r',linewidth=2) 14 15 def fx(x): 16 y=x**4-3*x+1 17 return y 18 x[0]=a 19 x[1]=b 20 for i in range(1000): 21 root=x[i+1]-(x[i+1]-x[i])/(fx(x[i+1])-fx(x[i]))*fx(x[i+1]) 22 x[i+2]=root 23 X.append(root) 24 #if (x[i+2]-x[i+1])<0.0001:计算一次即可 25 if x[i+2]==x[i+1]: 26 break 27 28 print('共迭代%d次'%i) 29 print('正割法求根的近似解序列为:',X) 30 print('正割法所求根为:',X[-1])