概率图模型是一类用图来表达变量相关关系的概率模型。它以图为表示工具，最常见的是用一个结点表示一个或一组随机变量，结点之间的边表示变量间的概率相关关系，即“变量关系图”。根据边的性质不同，概率图模型可大致分为两类：
1. 使用有向无环图表示变量间的依赖关系，称为有向图模型或贝叶斯网；
2. 使用无向图表示变量间的相关关系，称为无向图模型或马尔科夫网。
- 隐马尔科夫模型是结构最简单的动态贝叶斯网，这是一种著名的有向图模型，主要用于时序数据建模，在语音识别、自然语言处理等领域有广泛应用。
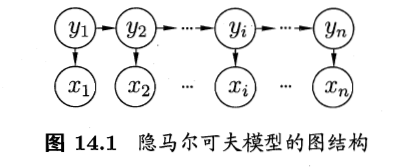
如上图所示，隐马尔可夫模型中的变量可分为两组：第一组是状态变量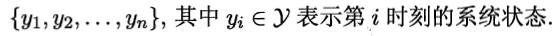
。通常假定状态变量是隐藏的、不可被观测的，因此状态变量亦称隐变量。第二组时观测变量
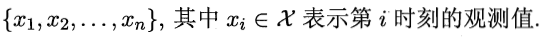在隐尔科夫模型中，系统通常在多个状态
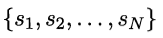之间转换，因此状态变量yi的取值范围Y（称为状态空间）通常是有N个可能取值的离散空间。观测变量xi可以使离散型也可以是连续型。
- 马尔科夫随机场是典型的马尔科夫网，这是一种著名的无向图模型。有一组势函数，亦称“因子”，这是定义在变量子集上的非负实函数，主要用于定义概率分布函数。
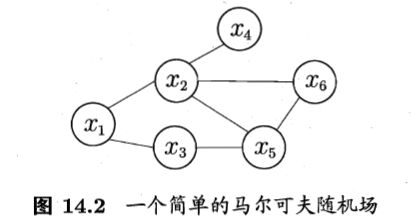
上图显示出一个简单的马尔可夫随机场，对于图中结点的一个子集，若其中任意两结点间都有边连接，则称该节点子集为一个团。若在一个团中加入另外任何一个结点都不再形成团，则称该团为“极大团”。换言之，极大团就是不能被其他团所包含的团，在图中
在马尔科夫随机场中，多个变量之间的联合概率分布能基于团分解为多个因子的乘积，每个因子仅与一个团相关。
- 条件随机场（CRF）：是一种判别式无向图模型，是对条件分布进行建模（ps：生成式模型是直接对联合分布进行建模）。以上两种隐马尔可夫模型和马尔科夫随机场都是生成式模型，而这个条件随机场则是判别式模型，试图对多个变量在给定观测值后的条件概率进行建模。
下面了解一下学习与推断~
概率图模型的推断：大致可分为两类。第一类是精确推断方法，希望能计算出目标变量的边际分布或条件分布的精确值；遗憾的是，一般情形下，此类算法的计算复杂度随着极大团规模的增长呈指数增长，适用范围有限；第二类是近似推断方法，希望在较低的时间复杂度下获得原问题的近似解，下面介绍一下两种代表性的精确推断方法，然后再介绍近似推断方法~
精确推断方法：
1. 变量消去：是一类动态规划算法，它利用图模型所描述的条件独立性来削减计算目标概率值所需的计算量，该方法是最直观的精确推断算法，也是构建其他精确推断算法的基础。
2. 信念传播：将变量消去法中的求和操作看作一个消息传递过程，较好地解决了求解多个边际分布时的重复计算问题。
近似推断：
1. MCMC采样（马尔科夫链蒙特卡罗方法）：我们关系某些概率分布并非因为对这些概率分布本身感兴趣，而是要基于它们计算某些期望，并且还可以进一步基于这些期望做出决策。直接计算或逼近这个期望比推断概率分布更容易。
2. 变分推断：通过使用已知简单分布来逼近需推断的复杂分布，并通过限制近似分布的类型，从而得到一种局部最优、但具有确定解的近似后验分布。
补充阅读：
话题模型：是一族生成式有向图模型，主要用于处理离散型的数据（如文本集合），在信息检索、自然语言处理等领域有广泛应用。----LDA是话题模型的典型代表。