深度学习研究的对象是具有深层表示的学习模型,它实际上是由两种不同的类型构成:
1.以神经网络为核心的深度神经网络;
2.以概率图模型为核心的深度图模型。
下面介绍深度概率图模型。---常用的深度图模型------玻尔兹曼机(Boltzmann Machine,BM)。
它是马尔科夫无向图网络中的一种,以顶点表示随机变量,边便是变量间的依赖关系。在深度学习领域中,玻尔兹曼机与自编码器一样,是深度学习中常见的预训练模型和无监督学习模型。BM是一个完全图结构,所有的结点通过无向边相连,它将节点集划分为可视层节点集V和隐藏层节点集H。其中,可是层,也称为输入层,用于接收可观察的样本数据集合;隐藏层则是对输入数据的抽象,通常能起到隐特征提取、降维等作用。下图表示的是由4个可视层神经元和3个隐藏层神经元构成,并且任意两个节点都有边相连,构成一个完全图结构。

BM具有强大的无监督学习能力,能够学习到输入数据中复杂的规则。但是无差别的无连接结构,使得其训练的代价非常昂贵。因此,在实际的应用中,更多的采用的是它的一种简化版变种网络:受限玻尔兹曼机。在这种网络结构中,进保留了可视层神经元与隐藏层神经元之间的连接,但可视层神经元之间,以及隐藏层神经元之间互不相连,这样就把网络结构从完全图简化为完全二分图。这种限制性的改造就构成该模型。
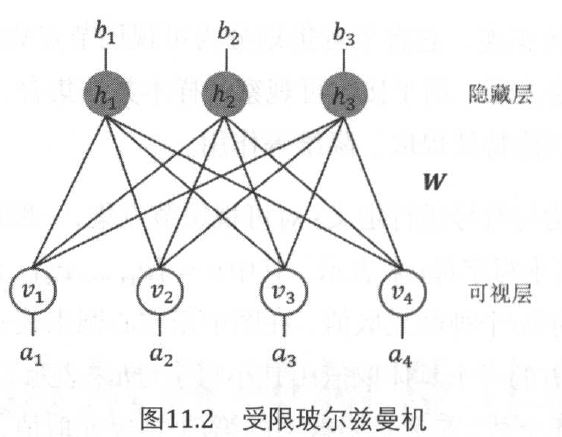
上图的受限玻尔兹曼机的每一个可视层神经元的输入数据类型,可以取二进制数据0或1,也可以取任意实数值。隐藏层单元是用来提取可视层数据的隐式特征,一般是二进制数值,当神经元的值为1的时候,称神经元处于激活状态;当神经元值为0的时候,称神经元处于非激活或抑制状态。隐藏层单元的取值服从伯努利分布。
相关模型--------能量模型:是概率图中一种具有普适意义的模型,能量的概念来源于物理学和热力学,用来描述一个物体的稳定性。
转化步骤:首先是先定义变量集的能量函数,然后根据能量函数得到每一个子团的势函数,最后根据无向图的马尔科夫独立性把势函数转化为随机变量的概率分布。
(1)能量函数:通过为随机变量集合定义一个能量值(标量),从而捕获该集合中随机变量间的依赖关系。如果一个随机变量组合被认为是合理的,则该变量组合也就越稳定,那么它应该具有较少的能量,也就是在所偏好的变量取值上有较小的能量值。
(2)从能量函数到势函数:势函数是一个非负函数,描述了变量集合间的相互关系。和能量函数类似,只是取值范围不同。
(3)从势函数到概率分布:在马尔科夫网络中,多个变量之间的联合概率分布是基于“最大团”分解为多个势函数的乘积。
表明:变量值的概率分布是关于能量函数,也就是说能量值越小,概率分布越大,从认知的角度来理解,就是说能量最小,则概率分布越大,也就是分布越合理。
补充阅读:
推荐系统,是连接用户和物品之间的桥梁,个性化推荐的形式化定义表述为:为特定的推荐产品形态或推荐场景下,构造合理的算法模型与系统架构,把正确的物品,在正确时间,推动给正确的用户。个性化推荐的应用场景非常广泛,包括:内容产业、电子商务、社交网络、广告精准投放等领域。
