Leetcode 第 217 场周赛

直接求就完事了

class Solution {
public:
    int maximumWealth(vector<vector<int>>& a) {
        int ans = 0;
        int temp = 0;
        for(auto &e:a){
            temp = 0;
            for(auto gg:e){
                temp += gg;
            }
            ans = max(ans, temp);
        }
        return ans;
    }
};

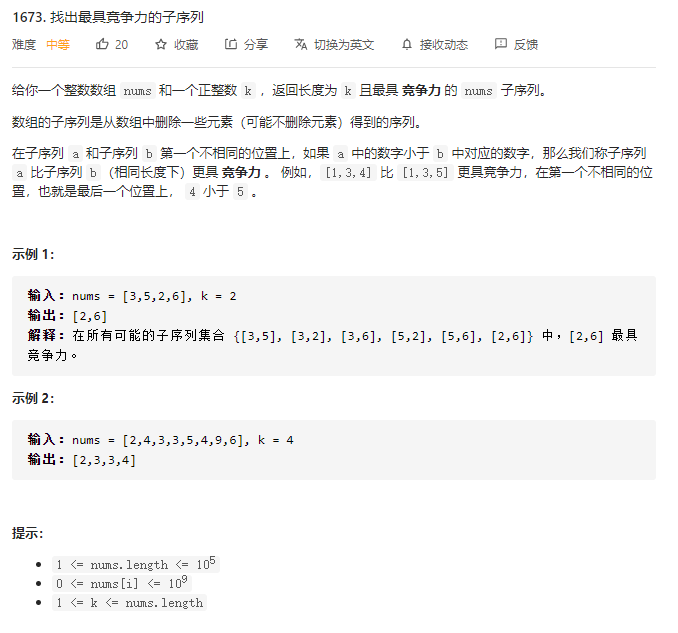
可知要使得前缀字典序最小，那么考虑使用单调栈
来使得栈内元素在每个能满足的位置都是最小的

class Solution {
public:
    vector<int> mostCompetitive(vector<int>& nums, int k) {
        vector<int> ans;
        int n = nums.size();
        for(int i=0; i<nums.size(); i++){
            while(ans.size()&&nums[i]<ans.back()&&ans.size()+(n-i)>k){
                ans.pop_back();
            }
            ans.push_back(nums[i]);
        }
        while(ans.size()>k) ans.pop_back();
        return ans;
    }
};

可以知道每一对能变成的范围是 2~2*limits
维护几个关键位置需要变几次，利用差分
然后扫一遍数组就可以求得答案

class Solution {
public:
    int minMoves(vector<int>& nums, int limits) {
        int n=nums.size();
        vector<int> sum(5*limits, 0);
        for(int i=0; 2*i<n; i++){
            int mi = min(nums[i], nums[n-i-1])+1;
            int ma = max(nums[i], nums[n-i-1])+limits;
            int zero = nums[i]+nums[n-i-1];
            sum[2] += 2;
            sum[mi] -= 2;
            sum[mi] += 1;
            sum[zero] -= 1;
            sum[zero+1] += 1;
            sum[ma+1] -= 1;
            sum[ma+1] += 2;
            
        }
        int ans = 1e8;
        int temp = 0;
        for(int i=2; i<=2*limits; i++){
            temp += sum[i];
            ans = min(ans, temp);
        }
        return ans;
    }
};

首先把所有数变成偶数 然后维护一个Set
那么我们可以知道，如果在前面将小数变得更小不会对答案产生更好的贡献
所以可以尝试着将最大值变小 每次取最后一个值，如果是偶数，则除2再插入
求一次最大差距 直到最大值是一个奇数

using ll = long long;
class Solution {
public:
    int minimumDeviation(vector<int>& nums) {
        int ans = 2147483647;
        set<int> se;
        for(auto e:nums){
           if(e&1) se.insert(e*2);
           else se.insert(e);
        }
        auto p = se.end();
        auto e = *--p;
        se.erase(p);
        while(true){
            p = se.end();
            if(e%2==0&&e>=*p)  e/=2;
            se.insert(e);
            p = se.end();
            ans = min(ans, (*--p) - (*se.begin()));
            e = *p;
            se.erase(p);
            if(e&1) break;
        }
     
        return ans;
    }
};