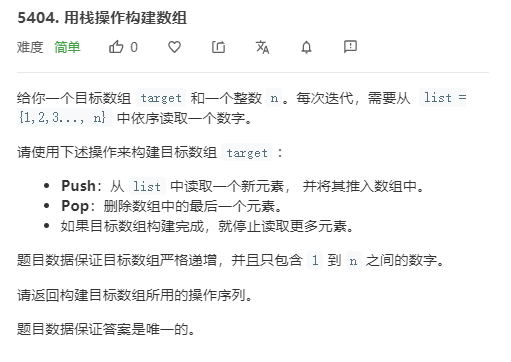
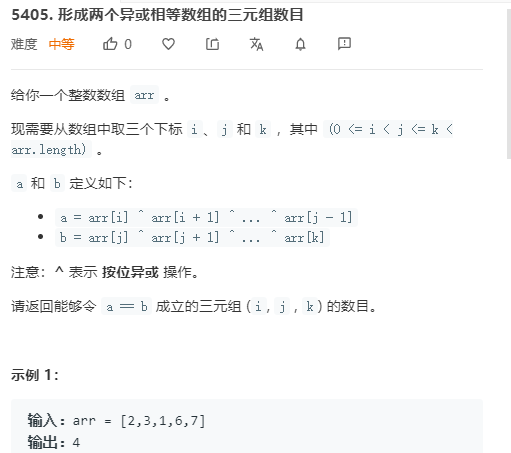
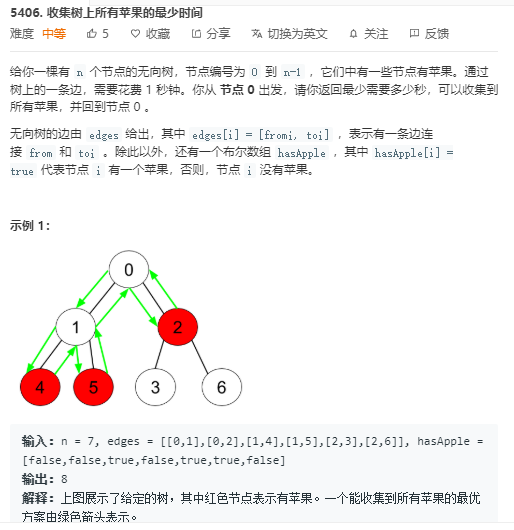
直接线性扫描就好
class Solution {
public:
vector<string> buildArray(vector<int>& target, int n) {
vector<string> ans;
int cur=1;
for(int i:target){
while(cur<i){
ans.push_back("Push");
ans.push_back("Pop");
cur++;
}
ans.push_back("Push");
cur++;
}
return ans;
}
};
一段连续的序列的异或为零,那么固定两端点为边界,中间点可以任意取
可以预处理前缀的异或,直接N^2遍历寻找左右边界即可
class Solution {
public:
int countTriplets(vector<int>& a){
int presum[301];
int ans=0;
for(int i=0; i<a.size(); i++)
presum[i+1]=presum[i]^a[i];
for(int i=1; i<a.size(); i++){
for(int k=i+1; k<=a.size(); k++)
if((presum[k]^presum[i-1])==0)
ans+=(k-i);
}
return ans;
}
};
仔细观察,会发现要走过的点刚好是一棵树
直接一遍dfs将所有子节点有苹果的点标记为有苹果
然后直接统计即可
class Solution {
public:
int minTime(int n, vector<vector<int>>& edges, vector<bool>& has) {
//建树然后深搜
// vector<int>(edges.size(),0);
bool vis[100000];
memset(vis,0,sizeof vis);
vector<int> g[100000];
for(auto e:edges){
g[e[0]].push_back(e[1]);
g[e[1]].push_back(e[0]);
}
vis[0]=1;
has[0] = dfs(0,has,g,vis);
int ans=0;
for(int i=0; i<has.size(); i++)
if(has[i]) ans++;
return ans>0?ans*2-2:0;
}
bool dfs(int cur,vector<bool>& has,vector<int>g[], bool vis[]){
int h=has[cur];
for(int i:g[cur]){
if(!vis[i]){
vis[i]=1;
h+=dfs(i,has,g,vis);
}
}
has[cur]=h;
return h;
}
};
操蛋了这么简单的记忆化搜索比赛的时候竟然没有写出来,害
直接记忆化搜索就好复杂度应该是O(mnk)
class Solution {
public:
int dp[55][55][15];
int sum[55][55]={0};
const int mod=1e9+7;
bool ck(int x1,int y1,int x2,int y2){
return sum[x2][y2]-sum[x1-1][y2]-sum[x2][y1-1]+sum[x1-1][y1-1]>0;
}
int dfs(int x1,int y1,int x2,int y2,int k){
if(k==0)return 1;
if(x1==x2&&y1==y2&&k)return 0;
if(dp[x1][y1][k]!=-1)return dp[x1][y1][k];
long long ans=0;
for(int i=x1+1;i<=x2;i++){
if(ck(x1,y1,i-1,y2)&&ck(i,y1,x2,y2))
ans+=dfs(i,y1,x2,y2,k-1);
ans%=mod;
}
for(int i=y1+1;i<=y2;i++){
if(ck(x1,y1,x2,i-1)&&ck(x1,i,x2,y2))
ans+=dfs(x1,i,x2,y2,k-1);
ans%=mod;
}
return dp[x1][y1][k]=ans;
}
int ways(vector<string>& pz, int k) {
int n=pz.size(),m=pz[0].size();
memset(dp,-1,sizeof(dp));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
sum[i][j]=(pz[i-1][j-1]=='A')+sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1];
}
}
if(k==1&&ck(1,1,n,m))return 1;
if(k==1)return 0;
return dfs(1,1,n,m,k-1);
}
};