Luogu3163 [CQOI2014]危桥
题意
有$n$个点和$m$条边,有些边可以无限次数的走,有些边这辈子只能走两次,给定两个起点和终点$a_1 --> a_2$(起点 --> 终点)和$b_1 --> b_2$(起点 --> 终点),询问是否可以让$a_1 --> a_2$往返$a_n$次,让$b_1 --> b_2$往返$b_n$次
题解
思路
思路还是比较好想的,就是原图连双向边,然后炒鸡源汇连$a_n*2$和$b_n*2$判断满流是否为$(a_n+b_n)*2$。
但是这样可以吗,不可以。
解决方案是把$b_1 和 b_2$反过来跑。
为什么呢?因为有可能$a_1$的流量可能会跑到$b_2$处。
于是下面给出说明。
反正就会发生这么一种情况:
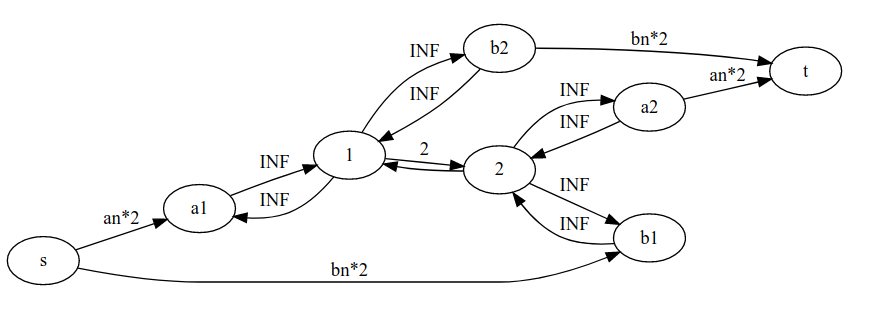
我们发现这张图的流量是满了,但是中间旁边就发现流量根本忽略了危桥,而且$a_1$的流量跑到了$b_2$那里。
所以我们直接把第二条路反过来,就是这样

然后发现就不会出现那种情况
一个细节
有人会说“如果危桥正向边反向边都有2的流量呢”?
然而我们证明一下发现这是不可能的。
证明:
如果出现了正向边反向边都有2的流量(或者一个为2一个为1),那么就说明$a_1 --> a_2$和$b_1 --> b_2$在危桥的路径上相反。也就是提取他们的路径刚好相反。
那么这种情况其实就是图1的情况,$a_1 --> a_2$要经过危桥的正向边$b_1 --> b_2$要经过危桥的反向边,然后就会发现$a_1$和$b_2$连在一起了,然后这个时候最小割应该是靠近源点的$(a_n+b_n)*2$而不是中间的$INF+INF+2*2$,而且中间根本不会有流量!所以这种情况下不会去流中间的边(根据最小割)。
代码如下:
然而由于数组没开足够大挂了半天......
1 #include <cstdio> 2 #include <cctype> 3 #include <cstring> 4 #include <iostream> 5 6 //User's Lib 7 8 using namespace std; 9 10 // #define DEBUG_PORT 11 #define DEBUG 12 13 #ifdef ONLINE_JUDGE 14 #undef DEBUG_PORT 15 #undef DEBUG 16 #endif 17 18 #ifdef DEBUG_PORT 19 #if __cplusplus >= 201103L 20 #ifdef DEBUG 21 template<typename T> 22 extern inline void Debug(T tar){ 23 cerr << tar << endl; 24 } 25 template<typename Head, typename T, typename... Tail> 26 extern inline void Debug(Head head, T mid, Tail... tail){ 27 cerr << head << ' '; 28 Debug(mid, tail...); 29 } 30 #else 31 # pragma GCC diagnostic push 32 # pragma GCC diagnostic ignored "-Wunused-parameter" 33 template<typename Head, typename T, typename... Tail> 34 extern inline void Debug(Head head, T mid, Tail... tail){ 35 return ; 36 } 37 # pragma GCC diagnostic pop 38 # pragma message "Warning : pragma used" 39 #endif 40 #else 41 # pragma message "Warning : C++11 Not Use" 42 #ifdef DEBUG 43 template <typename T> 44 extern inline void Debug(T tar){ 45 cerr << tar << endl; 46 } 47 #else 48 # pragma GCC diagnostic push 49 # pragma GCC diagnostic ignored "-Wunused-parameter" 50 template <typename T> 51 extern inline void Debug(T tar){ 52 return ; 53 } 54 # pragma GCC diagnostic pop 55 # pragma message "Warning : pragma used" 56 #endif 57 #endif 58 #else 59 # pragma GCC diagnostic push 60 # pragma GCC diagnostic ignored "-Wunused-parameter" 61 template<typename Head, typename T, typename... Tail> 62 extern inline void Debug(Head head, T mid, Tail... tail){ 63 return ; 64 } 65 template <typename T> 66 extern inline void Debug(T tar){ 67 return ; 68 } 69 # pragma GCC diagnostic pop 70 # pragma message "Warning : pragma used" 71 #endif 72 73 char buf[11111111], *pc = buf; 74 75 extern inline void Main_Init(){ 76 static bool INITED = false; 77 if(INITED) fclose(stdin), fclose(stdout); 78 else { 79 fread(buf, 1, 11111111, stdin); 80 INITED = true; 81 } 82 } 83 84 static inline int read(){ 85 int num = 0; 86 char c, sf = 1; 87 while(isspace(c = *pc++)); 88 if(c == 45) sf = -1, c = *pc ++; 89 while(num = num * 10 + c - 48, isdigit(c = *pc++)); 90 return num * sf; 91 } 92 93 namespace LKF{ 94 template <typename T> 95 extern inline T abs(T tar){ 96 return tar < 0 ? -tar : tar; 97 } 98 template <typename T> 99 extern inline void swap(T &a, T &b){ 100 T t = a; 101 a = b; 102 b = t; 103 } 104 template <typename T> 105 extern inline void upmax(T &x, const T &y){ 106 if(x < y) x = y; 107 } 108 template <typename T> 109 extern inline void upmin(T &x, const T &y){ 110 if(x > y) x = y; 111 } 112 template <typename T> 113 extern inline T max(T a, T b){ 114 return a > b ? a : b; 115 } 116 template <typename T> 117 extern inline T min(T a, T b){ 118 return a < b ? a : b; 119 } 120 } 121 122 //Source Code 123 124 /* 125 把原图往返看成经过两次 126 所以原图中起点和终点只有一个方向的流量这样子 127 然后危桥建单向边就可以了 128 同时为了防止出现什么起点和起点间的交易 129 所以跑一次之后再交换跑一次即可 130 证明博客:https://www.cnblogs.com/CreeperLKF/p/9176605.html 131 */ 132 133 const int MAXK = 55;///WTF...MAXN = 50炸了 134 const int MAXN = 66; 135 const int MAXM = 6666; 136 const int INF = 0x3f3f3f3f; 137 138 int n, m, s = MAXN - 10, t = s + 1; 139 140 struct Queue{ 141 int s, t; 142 int q[MAXN]; 143 Queue(){s = 1, t = 0;} 144 inline void clear(){ 145 s = 1, t = 0; 146 } 147 inline bool empty(){ 148 return s > t; 149 } 150 inline int size(){ 151 return t - s + 1; 152 } 153 inline void push(int tar){ 154 q[++ t] = tar; 155 } 156 inline int front(){ 157 return q[s]; 158 } 159 inline void pop(){ 160 s ++; 161 } 162 }; 163 164 struct Graph{ 165 int tot; 166 int beginx[MAXN], endx[MAXM], nxt[MAXM], res[MAXM]; 167 Graph(){ 168 tot = 1; 169 } 170 inline void Init(){ 171 tot = 1; 172 memset(beginx, 0, sizeof(beginx)); 173 } 174 inline void add_edge(int u, int v, int r){ 175 // Debug(u, "->", v, "[label = "", r, ""]");//Debug... 176 nxt[++ tot] = beginx[u], beginx[u] = tot, endx[tot] = v, res[tot] = r; 177 nxt[++ tot] = beginx[v], beginx[v] = tot, endx[tot] = u, res[tot] = 0; 178 } 179 }; 180 181 struct ISap{ 182 Graph g; 183 Queue mession; 184 int max_f; 185 int cur[MAXN], d[MAXN], num[MAXN], pre[MAXN]; 186 inline void bfs(){ 187 mession.clear(); 188 mession.push(t); 189 memset(d, 0, sizeof(d)); 190 memset(num, 0, sizeof(num)); 191 d[t] = 1; 192 int u, v; 193 while(!mession.empty()){ 194 u = mession.front(); 195 mession.pop(); 196 num[d[u]] ++; 197 for(int i = g.beginx[u]; i; i = g.nxt[i]){ 198 v = g.endx[i]; 199 if(!d[v] && g.res[i ^ 1]){ 200 d[v] = d[u] + 1; 201 mession.push(v); 202 } 203 } 204 } 205 } 206 inline int dfs(int u, int now_f){ 207 if(u == t) return now_f; 208 int ret_f = 0; 209 for(int &i = cur[u]; i; i = g.nxt[i]){ 210 int v = g.endx[i]; 211 if(g.res[i] && d[u] == d[v] + 1){ 212 int ret = dfs(v, min(g.res[i], now_f)); 213 ret_f += ret, now_f -= ret; 214 g.res[i] -= ret, g.res[i ^ 1] += ret; 215 if(d[s] >= MAXN - 4 || !now_f) return ret_f; 216 } 217 } 218 if(-- num[d[u]] == 0) d[s] = MAXN - 4; 219 ++ num[++ d[u]]; 220 cur[u] = g.beginx[u]; 221 return ret_f; 222 } 223 inline int ISAP(){ 224 bfs(); 225 max_f = 0; 226 memcpy(cur, g.beginx, sizeof(cur)); 227 while(d[s] < MAXN - 5) 228 max_f += dfs(s, INF); 229 return max_f; 230 } 231 }isap; 232 233 int a1, a2, an, b1, b2, bn; 234 int matrix[MAXK][MAXK]; 235 236 int main(){ 237 Main_Init(); 238 while((n = read()) > 0){ 239 a1 = read() + 1, a2 = read() + 1, an = read() << 1; 240 b1 = read() + 1, b2 = read() + 1, bn = read() << 1; 241 memset(matrix, 0, sizeof(matrix)); 242 for(int i = 1; i <= n; i++){ 243 while(isspace(*pc ++)); 244 pc --; 245 for(int j = 1; j <= n; j++){ 246 char c = *pc ++; 247 switch(c){ 248 case 'O': matrix[i][j] = 1; break; 249 case 'N': matrix[i][j] = 2; break; 250 } 251 } 252 } 253 254 isap.g.Init(); 255 isap.g.add_edge(s, a1, an), isap.g.add_edge(a2, t, an); 256 isap.g.add_edge(s, b1, bn), isap.g.add_edge(b2, t, bn); 257 for(int i = 1; i <= n; i++) 258 for(int j = 1; j <= n; j++) 259 if(matrix[i][j]) 260 isap.g.add_edge(i, j, matrix[i][j] & 1 ? 2 : INF); 261 if(isap.ISAP() != an + bn){ 262 puts("No"); 263 continue; 264 } 265 266 isap.g.Init(); 267 isap.g.add_edge(s, a1, an), isap.g.add_edge(a2, t, an); 268 isap.g.add_edge(s, b2, bn), isap.g.add_edge(b1, t, bn); 269 for(int i = 1; i <= n; i++) 270 for(int j = 1; j <= n; j++) 271 if(matrix[i][j]) 272 isap.g.add_edge(i, j, matrix[i][j] & 1 ? 2 : INF); 273 puts(isap.ISAP() == an + bn ? "Yes" : "No");//大小写...... 274 } 275 Main_Init(); 276 return 0; 277 }