CF809C Find a car

https://www.luogu.org/problemnew/show/CF809C

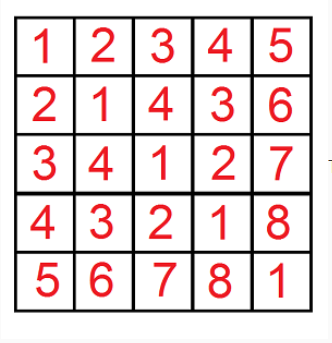
这个题的难点主要在于看出这个矩阵所有数字-1后，第i行第j列就等于i^j。

这个规律对着这个表，观察一会大概是可以观察出来的。

然后就是容斥+数位dp求解即可。

#include<bits/stdc++.h>
#define N 1100
#define eps 1e-7
#define inf 1e9+7
#define db double
#define ll long long
#define ldb long double
using namespace std;
inline int read()
{
	char ch=0;
	int x=0,flag=1;
	while(!isdigit(ch)){ch=getchar();if(ch=='-')flag=-1;}
	while(isdigit(ch)){x=(x<<3)+(x<<1)+ch-'0';ch=getchar();}
	return x*flag;
}
const int mo=1e9+7;
void add(int &x,int k){x=(x+k)%mo;}
int f[N],g[N],h[N],dp[2][2][2],DP[2][2][2],dp_[2][2][2],DP_[2][2][2];
int solve()
{
	memset(dp,0,sizeof(dp));
	memset(DP,0,sizeof(DP));
	memset(dp_,0,sizeof(dp_));
	memset(DP_,0,sizeof(DP_));
	dp[0][0][0]=1;DP[0][0][0]=0;
	for(int i=1;i<=31;i++)
	{
		int w=(1<<(30-i+1))%mo; 
		for(int a=0;a<=1;a++)
		for(int b=0;b<=1;b++)
		for(int c=0;c<=1;c++)
		if(dp[a][b][c]||DP[a][b][c])
		for(int x=0;x<=(a?1:f[i]);x++)
		for(int y=0;y<=(b?1:g[i]);y++)
		if((x^y)<=(c?1:h[i]))
		{
			int o=dp[a][b][c],t=DP[a][b][c];
			add(dp_[a|(x<f[i])][b|(y<g[i])][c|((x^y)<h[i])],o);
			add(DP_[a|(x<f[i])][b|(y<g[i])][c|((x^y)<h[i])],((1ll*(x^y)*o*w%mo)+t)%mo);
		}
		for(int a=0;a<=1;a++)
		for(int b=0;b<=1;b++)
		for(int c=0;c<=1;c++)
		{
			dp[a][b][c]=dp_[a][b][c];dp_[a][b][c]=0;
			DP[a][b][c]=DP_[a][b][c];DP_[a][b][c]=0;
		}
	}
	int ans=0;
	for(int a=0;a<=1;a++)
	for(int b=0;b<=1;b++)
	for(int c=0;c<=1;c++)
	ans=(ans+((dp[a][b][c]+DP[a][b][c])%mo))%mo;
	return (ans%mo+mo)%mo;
}
void work()
{
	int a=read()-1,b=read()-1,c=read()-1,d=read()-1,k=read()-1,ans=0;
	for(int i=30;i>=0;i--)h[30-i+1]=((1<<i)&(k))?1:0;
	if(c>=0&&d>=0)
	{
		for(int i=30;i>=0;i--)f[30-i+1]=((1<<i)&(c))?1:0;
		for(int i=30;i>=0;i--)g[30-i+1]=((1<<i)&(d))?1:0;
		ans=(ans+solve())%mo;
	}
	if(a-1>=0&&d>=0)
	{
		for(int i=30;i>=0;i--)f[30-i+1]=((1<<i)&(a-1))?1:0;
		for(int i=30;i>=0;i--)g[30-i+1]=((1<<i)&(d))?1:0;
		ans=(ans-solve())%mo;
	}
	if(c>=0&&b-1>=0)
	{
		for(int i=30;i>=0;i--)f[30-i+1]=((1<<i)&(c))?1:0;
		for(int i=30;i>=0;i--)g[30-i+1]=((1<<i)&(b-1))?1:0;
		ans=(ans-solve())%mo;
	}	
	if(a-1>=0&&b-1>=0)
	{
		for(int i=30;i>=0;i--)f[30-i+1]=((1<<i)&(a-1))?1:0;
		for(int i=30;i>=0;i--)g[30-i+1]=((1<<i)&(b-1))?1:0;
		ans=(ans+solve())%mo;
	}
	printf("%d
",(ans%mo+mo)%mo);
}
int main()
{
	int t=read();
	for(int i=1;i<=t;i++)work();
	return 0;
}