图形学基础（一）光栅图形学_下：剪裁

c++,MFC,VS2017

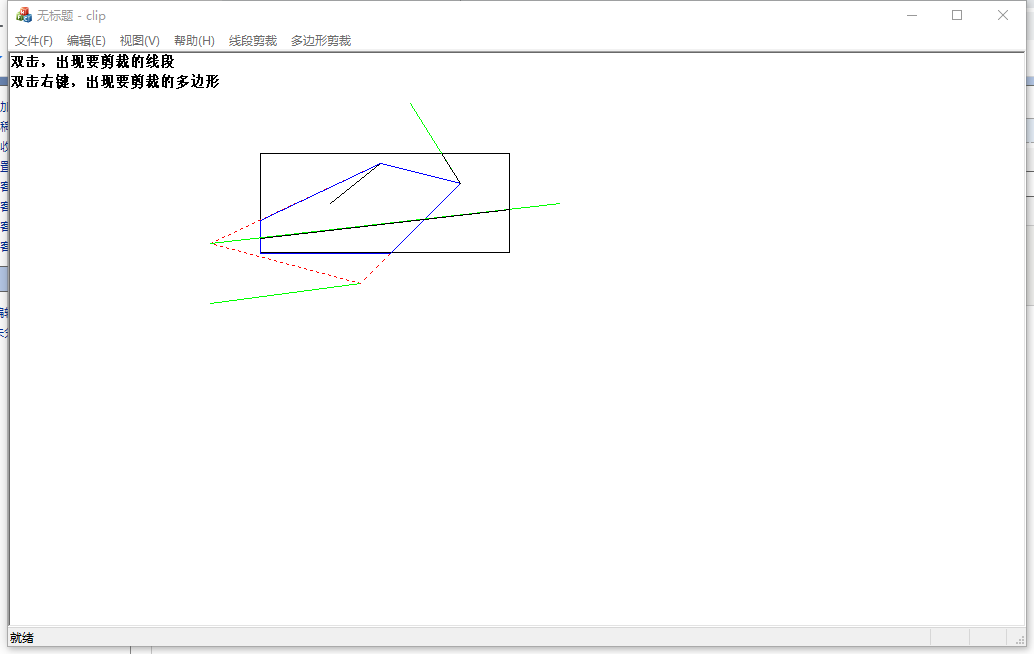
准备（矩形，线段，多边形）

void CclipView::OnDraw(CDC* pDC)
{
    CclipDoc* pDoc = GetDocument();
    ASSERT_VALID(pDoc);
    if (!pDoc)
        return;

    // TODO: 在此处为本机数据添加绘制代码
    CPen newpen(PS_SOLID, 1, RGB(0, 0, 0));
    CPen *old = pDC->SelectObject(&newpen);
    pDC->Rectangle(CRect(Xmin, Ymax, Xmax, Ymin));//矩形
    ptset[0] = CPoint(320, 150);
    ptset[1] = CPoint(370, 110);
    ptset[2] = CPoint(200, 190);
    ptset[3] = CPoint(550, 150);
    ptset[4] = CPoint(200, 250);
    ptset[5] = CPoint(350, 230);
    ptset[6] = CPoint(400, 50);
    ptset[7] = CPoint(450, 130);
    pDC->TextOutW(0, 0, TEXT("双击，出现要剪裁的线段"));
    pDC->TextOutW(0, 20, TEXT("双击右键，出现要剪裁的多边形"));
    pDC->SelectObject(old);
}

void CclipView::OnLButtonDblClk(UINT nFlags, CPoint point)//线段
{
    // TODO: 在此添加消息处理程序代码和/或调用默认值
    flag = 1;
    CDC* pDC = GetDC(); 
    CPen newpen(PS_SOLID, 1, RGB(0, 255, 0));
    CPen *old = pDC->SelectObject(&newpen);
    for (int i = 0; i < N; i++) {
        pDC->MoveTo(ptset[i]);
        pDC->LineTo(ptset[i + 1]);
        i++;
    }
    
    CView::OnLButtonDblClk(nFlags, point);
}

void CclipView::OnRButtonDblClk(UINT nFlags, CPoint point)//多边形
{
    // TODO: 在此添加消息处理程序代码和/或调用默认值
    flag = 1;
    CDC* pDC = GetDC();
    CPen newpen(PS_DOT, 1, RGB(255, 0, 0));
    CPen *old = pDC->SelectObject(&newpen);
    pt[0] = ptset[1]; pt[1] = ptset[7]; pt[2] = ptset[5]; pt[3] = ptset[2]; pt[4] = ptset[1];
    pDC->MoveTo(ptset[1]);
    pDC->LineTo(ptset[7]);
    pDC->LineTo(ptset[5]);
    pDC->LineTo(ptset[2]);
    pDC->LineTo(ptset[1]);
    CView::OnRButtonDblClk(nFlags, point);
}

直线段剪裁（Cohen-Sutherland算法 / Liang-Barsky算法）

（默认矩形窗口）

1、Cohen-Sutherland算法

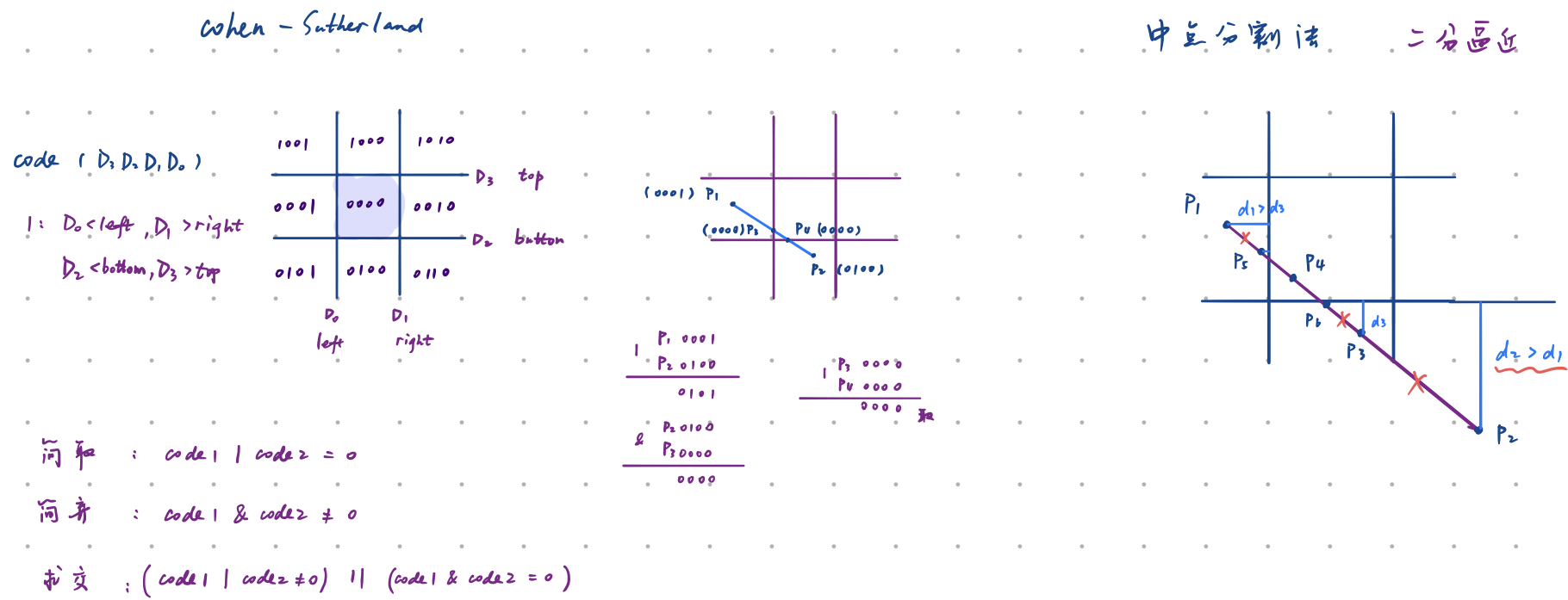
 以窗口的矩形为中心，形成一个九宫格，窗口左：0001，窗口右：0010，窗口下：0100，窗口上：1000，其余均由或运算得到。中点分割法是对Cohen-Sutherland算法的改进。（四次求交，全部舍弃。）

 步骤：为线段的端点编码 -> 由端点位置决定简取、简弃、求交 -> [ 更新两端点 -> ] 画线

void CclipView::OnClipline()
{
    // TODO: 在此添加命令处理程序代码
    CDC* pDC = GetDC();
    CPen newpen(PS_SOLID, 1, RGB(0, 0, 0));
    CPen *old = pDC->SelectObject(&newpen);
    if (flag != 1) {
        MessageBox(TEXT("请先双击"), TEXT("警告!"));
    }
    else {
        float x, y, x1, x2, y1, y2;
        int i, code1, code2;
        //求两端点的区号
        for (i = 0; i < N; i++, i++) {
            int c = 0;
            if (ptset[i].x < Xmin)    c = c | LEFT;
            else if (ptset[i].x > Xmax)    c = c | RIGHT;
            if (ptset[i].y > Ymin)    c = c | BOTTOM;
            else if (ptset[i].y < Ymax)    c = c | TOP;
            code1 = c; c = 0;
            if (ptset[i + 1].x < Xmin)    c = c | LEFT;
            else if (ptset[i + 1].x > Xmax)    c = c | RIGHT;
            if (ptset[i + 1].y > Ymin)    c = c | BOTTOM;
            else if (ptset[i + 1].y < Ymax)    c = c | TOP;
            code2 = c;
            //线段与区域相交
            if (code1 != 0 && code2 != 0 && (code1&code2) == 0) { //端点全在框外
                if ((LEFT&code1) != 0) {//与左边界交
                    x = Xmin;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmin - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                } else if ((RIGHT&code1) != 0) {//与右边界交
                    x = Xmax;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmax - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                } else if ((BOTTOM&code1) != 0) {//与下边界交
                    y = Ymin;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymin - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                } else if ((TOP&code1) != 0) {//与上边界交
                    y = Ymax;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymax - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                }
                ptset[i].x = x; ptset[i].y = y;
                if ((LEFT&code2) != 0) {//与左边界交
                    x = Xmin;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmin - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                }
                else if ((RIGHT&code2) != 0) {//与右边界交
                    x = Xmax;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmax - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                }
                else if ((BOTTOM&code2) != 0) {//与下边界交
                    y = Ymin;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymin - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                }
                else if ((TOP&code2) != 0) {//与上边界交
                    y = Ymax;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymax - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                }
                ptset[i + 1].x = x; ptset[i + 1].y = y;
                pDC->MoveTo(ptset[i].x, ptset[i].y);
                pDC->LineTo(ptset[i + 1].x, ptset[i + 1].y);
            }
            if (code1 == 0 && code2 == 0) {    //端点全在框内
                pDC->MoveTo(ptset[i].x, ptset[i].y);
                pDC->LineTo(ptset[i + 1].x, ptset[i + 1].y);
            }
            if (code1 == 0 && code2 != 0) {
                if ((LEFT&code2) != 0) {//与左边界交
                    x = Xmin;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmin - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                }
                else if ((RIGHT&code2) != 0) {//与右边界交
                    x = Xmax;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmax - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                }
                else if ((BOTTOM&code2) != 0) {//与下边界交
                    y = Ymin;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymin - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                }
                else if ((TOP&code2) != 0) {//与上边界交
                    y = Ymax;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymax - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                }
                ptset[i + 1].x = x; ptset[i + 1].y = y;
                pDC->MoveTo(ptset[i].x, ptset[i].y);
                pDC->LineTo(ptset[i + 1].x, ptset[i + 1].y);
            }
            if (code1 != 0 && code2 == 0) {
                if ((LEFT&code1) != 0) {//与左边界交
                    x = Xmin;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmin - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                }
                else if ((RIGHT&code1) != 0) {//与右边界交
                    x = Xmax;
                    y = ptset[i].y + (ptset[i + 1].y - ptset[i].y)*(Xmax - ptset[i].x) / (ptset[i + 1].x - ptset[i].x);
                }
                else if ((BOTTOM&code1) != 0) {//与下边界交
                    y = Ymin;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymin - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                }
                else if ((TOP&code1) != 0) {//与上边界交
                    y = Ymax;
                    x = ptset[i].x + (ptset[i + 1].x - ptset[i].x)*(Ymax - ptset[i].y) / (ptset[i + 1].y - ptset[i].y);
                }
                ptset[i].x = x; ptset[i].y = y;
                pDC->MoveTo(ptset[i + 1].x, ptset[i + 1].y);
                pDC->LineTo(ptset[i].x, ptset[i].y);
            }
        }        
    }
}

2、Liang-Barsky算法

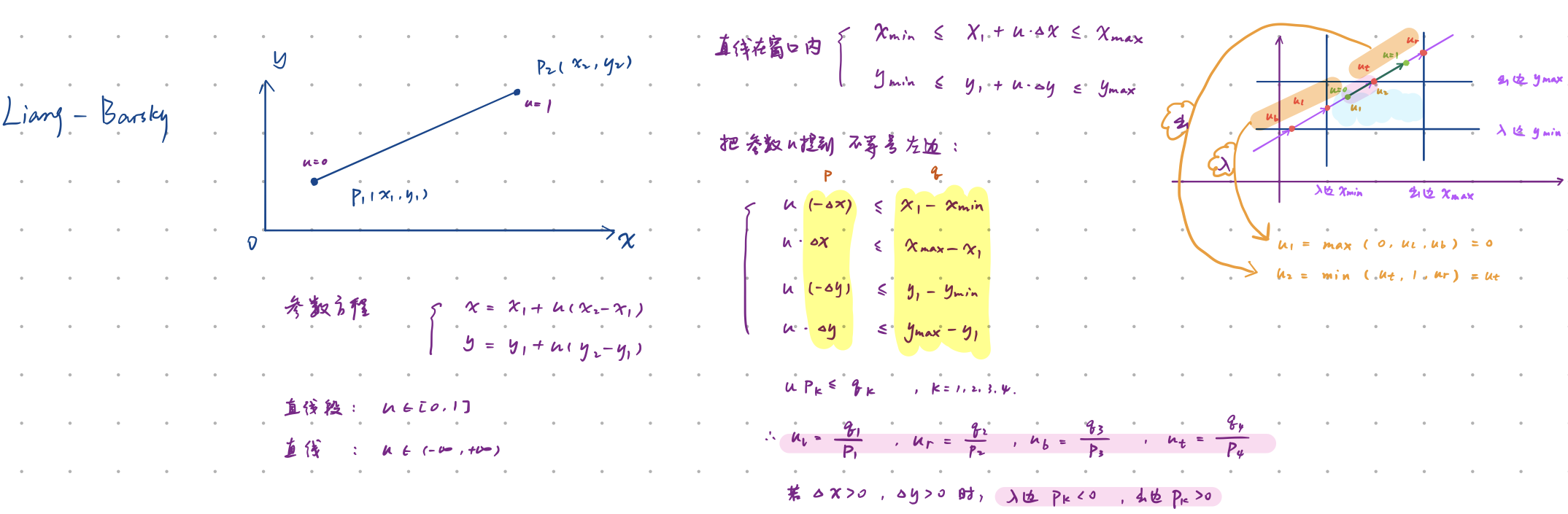
 二维参数表示一条直线段，把线段看成有向的，每次都要算出直线与四条边的交点，入边、出边由 P 的正负判断。

 步骤：求交 -> 每次选取两点max（入边交点1，入边交点2，向量始点），min（出边交点1，出边交点2，向量终点）-> 画线

多边形剪裁（Sutherland-Hodgman算法）

1、Sutherland-Hodgman算法

 步骤：用左右下上四条边切割原图形，切割时通过两点位置，判断该有向线段简取/求交，初取时取两点，后每次取可见侧向量终点（可能是交点）。

void CclipView::OnClippolygon()
{
    // TODO: 在此添加命令处理程序代码
    CDC* pDC = GetDC();
    CPen newpen(PS_SOLID, 1, RGB(0, 0, 255));
    CPen *old = pDC->SelectObject(&newpen);
    if (flag != 1) {
        MessageBox(TEXT("请先双击右键"), TEXT("警告!"));
    } else {
        int i, k; 
        int code1, code2;
        k = 0;
        for (i = 0; i < M-1; i++) {// L
            if (pt[i].x < Xmin)    code1 = LEFT;
            else if (pt[i].x > Xmin)    code1 = 0;
            if (pt[i + 1].x < Xmin)    code2 = LEFT;
            else if (pt[i + 1].x > Xmin)    code2 = 0;
            if (code1 != 0 && code2 == 0) {
                p[k].x = Xmin;
                p[k].y = pt[i].y + (pt[i + 1].y - pt[i].y)*(Xmin - pt[i].x) / (pt[i + 1].x - pt[i].x);
                p[k + 1].x = pt[i + 1].x; p[k + 1].y = pt[i + 1].y;
                k = k + 2;
            }
            if (code1 == 0 && code2 == 0) {
                if (k == 0) {
                    p[k].x = pt[i].x; p[k].y = pt[i].y;
                    p[k + 1].x = pt[i + 1].x; p[k + 1].y = pt[i + 1].y;
                    k = k + 2;
                } else {
                    p[k].x = pt[i + 1].x; p[k].y = pt[i + 1].y;
                    k = k + 1;
                }
            }
            if (code1 == 0 && code2 != 0) {
                p[k].x = Xmin;
                p[k].y = pt[i].y + (pt[i + 1].y - pt[i].y)*(Xmin - pt[i].x) / (pt[i + 1].x - pt[i].x);
                k = k + 1;
            }
        }
        M = k; k = 0;
        for (i = 0; i < M-1; i++) {// R
            if (p[i].x < Xmax)    code1 = 0;
            else if (p[i].x > Xmax)    code1 = RIGHT;
            if (p[i + 1].x < Xmax)    code2 = 0;
            else if (p[i + 1].x > Xmax)    code2 = RIGHT;
            if (code1 != 0 && code2 == 0) {
                pt[k].x = Xmax;
                pt[k].y = p[i].y + (p[i + 1].y - p[i].y)*(Xmax - p[i].x) / (p[i + 1].x - p[i].x);
                pt[k + 1].x = p[i + 1].x; pt[k + 1].y = p[i + 1].y;
                k = k + 2;
            }
            if (code1 == 0 && code2 == 0) {
                if (k == 0) {
                    pt[k].x = p[i].x; pt[k].y = p[i].y;
                    pt[k + 1].x = p[i + 1].x; pt[k + 1].y = p[i + 1].y;
                    k = k + 2;
                }
                else {
                    pt[k].x = p[i + 1].x; pt[k].y = p[i + 1].y;
                    k = k + 1;
                }
            }
            if (code1 == 0 && code2 != 0) {
                pt[k].x = Xmax;
                pt[k].y = p[i].y + (p[i + 1].y - p[i].y)*(Xmax - p[i].x) / (p[i + 1].x - p[i].x);
                k++;
            }
        }
        M = k; k = 0;    
        for (i = 0; i < M-1; i++) {// B
            if (pt[i].y > Ymin)    code1 = BOTTOM;
            else if (pt[i].y < Ymin)    code1 = 0;
            if (pt[i + 1].y > Ymin)    code2 = BOTTOM;
            else if (pt[i + 1].y < Ymin)    code2 = 0;
            if (code1 != 0 && code2 == 0) {
                p[k].y = Ymin;
                p[k].x = pt[i].x + (pt[i + 1].x - pt[i].x)*(Ymin - pt[i].y) / (pt[i + 1].y - pt[i].y);
                p[k + 1].x = pt[i + 1].x; p[k + 1].y = pt[i + 1].y;
                k = k + 2;
            }
            if (code1 == 0 && code2 == 0) {
                if (k == 0) {
                    p[k].x = pt[i].x; p[k].y = pt[i].y;
                    p[k + 1].x = pt[i + 1].x; p[k + 1].y = pt[i + 1].y;
                    k = k + 2;
                }
                else {
                    p[k].x = pt[i + 1].x; p[k].y = pt[i + 1].y;
                    k = k + 1;
                }
            }
            if (code1 == 0 && code2 != 0) {
                p[k].y = Ymin;
                p[k].x = pt[i].x + (pt[i + 1].x - pt[i].x)*(Ymin - pt[i].y) / (pt[i + 1].y - pt[i].y);
                k++;
            }
        }
        M = k; k = 0;
        for (i = 0; i < M-1; i++) {// T
            if (p[i].y > Ymax)    code1 = 0;
            else if (p[i].y < Ymax)    code1 = 0;
            if (p[i + 1].y > Ymax)    code2 = 0;
            else if (p[i + 1].y < Ymax)    code2 = TOP;
            if (code1 != 0 && code2 == 0) {
                pt[k].y = Ymax;
                pt[k].x = p[i].x + (p[i + 1].x - p[i].x)*(Ymax - p[i].y) / (p[i + 1].y - p[i].y);
                pt[k + 1].x = p[i + 1].x; pt[k + 1].y = p[i + 1].y;
                k = k + 2;
            }
            if (code1 == 0 && code2 == 0) {
                if (k == 0) {
                    pt[k].x = p[i].x; pt[k].y = p[i].y;
                    pt[k + 1].x = p[i + 1].x; pt[k + 1].y = p[i + 1].y;
                    k = k + 2;
                }
                else {
                    pt[k].x = p[i + 1].x; pt[k].y = p[i + 1].y;
                    k = k + 1;
                }
            }
            if (code1 == 0 && code2 != 0) {
                pt[k].y = Ymax;
                pt[k].x = p[i].x + (p[i + 1].x - p[i].x)*(Ymax - p[i].y) / (p[i + 1].y - p[i].y);
                k++;
            }
        }
        M = k;
        pDC->MoveTo(pt[0]);
        for (int j = 1; j < M; j++) {
            pDC->LineTo(pt[j]);
        }
    }
}

2、ex：Weiler-Atherton算法

先这样吧，以后再加。

参考资料：

1、《计算机图形学原理及算法教程》和青芳 编著

2、计算机图形学 - 中国农业大学 赵明 

本文采用CC BY 4.0知识共享许可协议。