HDU 1724 Ellipse 【自适应Simpson积分】

Ellipse

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 1977    Accepted Submission(s): 832

Problem Description

Math is important!! Many students failed in 2+2’s mathematical test, so let's AC this problem to mourn for our lost youth..
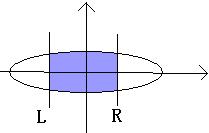
Look this sample picture:



A ellipses in the plane and center in point O. the L,R lines will be vertical through the X-axis. The problem is calculating the blue intersection area. But calculating the intersection area is dull, so I have turn to you, a talent of programmer. Your task is tell me the result of calculations.(defined PI=3.14159265 , The area of an ellipse A=PI*a*b )

 

Input

Input may contain multiple test cases. The first line is a positive integer N, denoting the number of test cases below. One case One line. The line will consist of a pair of integers a and b, denoting the ellipse equation , A pair of integers l and r, mean the L is (l, 0) and R is (r, 0). (-a <= l <= r <= a).

 

Output

For each case, output one line containing a float, the area of the intersection, accurate to three decimals after the decimal point.

 

Sample Input

2 2 1 -2 2 2 1 0 2

 

Sample Output

6.283 3.142

 

Author

威士忌

 

Source

HZIEE 2007 Programming Contest

题目链接：

　　http://acm.hdu.edu.cn/showproblem.php?pid=1724

题目大意：

　　求椭圆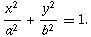被x=l,x=r两条线所围区域面积。

题目思路：

　　【自适应Simpson积分】

　　首先易得上半部分面积积分公式为sqrt(b²(1-x²/a²))

　　接下来就是套用自适应Simpson积分即可。eps一开始设为1e-4就行。

　　一道模板题。

/****************************************************
    
    Author : Coolxxx
    Copyright 2017 by Coolxxx. All rights reserved.
    BLOG : http://blog.csdn.net/u010568270
    
****************************************************/
#include<bits/stdc++.h>
#pragma comment(linker,"/STACK:1024000000,1024000000")
#define abs(a) ((a)>0?(a):(-(a)))
#define lowbit(a) (a&(-a))
#define sqr(a) ((a)*(a))
#define mem(a,b) memset(a,b,sizeof(a))
const double eps=1e-8;
const int J=10000;
const int mod=1000000007;
const int MAX=0x7f7f7f7f;
const double PI=3.14159265358979323;
const int N=104;
using namespace std;
typedef long long LL;
double anss;
LL aans;
int cas,cass;
int n,m,lll,ans;
double a,b;
double F(double x)//原函数f(x)
{
    return sqrt(b*b*(1-x*x/(a*a)));
}
double simpson(double a,double b)//求simpson公式S(a,b)
{
    double mid=(a+b)/2;
    return (b-a)/6*(F(a)+4*F(mid)+F(b));
}
double simpson(double l,double r,double eps,double A)//自适应simpson积分过程
{
    double mid=(l+r)/2;
    double L=simpson(l,mid);
    double R=simpson(mid,r);
    if(abs(L+R-A)<=15*eps)return L+R+(L+R-A)/15.0;//eps为精度需求
    return simpson(l,mid,eps/2,L)+simpson(mid,r,eps/2,R);
}
double simpson(double l,double r,double eps)//自适应simpson积分
{
    return simpson(l,r,eps,simpson(l,r));
}
int main()
{
    #ifndef ONLINE_JUDGE
//    freopen("1.txt","r",stdin);
//    freopen("2.txt","w",stdout);
    #endif
    int i,j,k;
    double x,y,z;
//    for(scanf("%d",&cass);cass;cass--)
    for(scanf("%d",&cas),cass=1;cass<=cas;cass++)
//    while(~scanf("%s",s))
//    while(~scanf("%d",&n))
    {
        scanf("%lf%lf%lf%lf",&a,&b,&x,&y);
        printf("%.3lf
",simpson(x,y,1e-4)*2);
    }
    return 0;
}
/*
//

//
*/