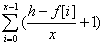[spfa] Jzoj P4722 跳楼机

Description

 
DJL为了避免成为一只咸鱼，来找srwudi学习压代码的技巧。
Srwudi的家是一幢h层的摩天大楼。由于前来学习的蒟蒻越来越多，srwudi改造了一个跳楼机，使得访客可以更方便的上楼。
经过改造，srwudi的跳楼机可以采用以下四种方式移动：
1、向上移动x层；
2、向上移动y层；
3、向上移动z层；
4、回到第一层。
一个月黑风高的大中午，DJL来到了srwudi的家，现在他在srwudi家的第一层，碰巧跳楼机也在第一层。DJL想知道，他可以乘坐跳楼机前往的楼层数。

 

Input

第一行一个整数h，表示摩天大楼的层数。
第二行三个正整数，分别表示题目中的x, y, z。

Output

一行一个整数，表示DJL可以到达的楼层数。

 

Sample Input

15
4 7 9

Sample Output

9
样例解释
可以到达的楼层有：1,5,8,9,10,12,13,14,15

 

Data Constraint

对于20%的数据，1≤h, x, y, z≤100；
对于40%的数据，1≤h, x, y, z≤10^5；
对于100%的数据，1≤h≤10^18，1≤x, y, z≤10^5。

题解

• 首先，我们知道，如果a可以到达，那么也可以到达
• 那么，一个到达的高度l=ax+by+cz
• 可以先不考虑x，设f[i]为到模x下高度i的可以到达的最小楼层
• 如果我们得到了所有f，答案就是
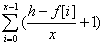
• 那么如果不考虑x的话，就只有两种转移：
• ①f[(i+y)%x]=f[i]+y
• ②f[(i+z)%x]=f[i]+z
• 也就是一个最短路模型，直接spfa（这题居然不卡spfa）

代码

#include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
queue<int> Q;
struct edge {int to,from,v;}e[200010];
long long dis[100010],ans,h;
int x,y,z,cnt,visit[100010],head[100010];
void insert(int x,int y,int v) { e[++cnt].to=y; e[cnt].from=head[x]; e[cnt].v=v; head[x]=cnt; }
void spfa(int s)
{
    memset(dis,-1,sizeof(dis));
    dis[s]=visit[s]=1; Q.push(s);
    while (!Q.empty())
    {
        int u=Q.front(); Q.pop();
        visit[u]=0;
        for (int i=head[u];i;i=e[i].from)
            if (dis[e[i].to]==-1||dis[e[i].to]>dis[u]+e[i].v)
            {
                dis[e[i].to]=dis[u]+e[i].v;
                if (!visit[e[i].to]) visit[e[i].to]=1,Q.push(e[i].to);
            }
    }
}
int main()
{
    scanf("%lld%d%d%d",&h,&x,&y,&z);
    for (int i=0;i<x;i++) insert(i,(i+y)%x,y),insert(i,(i+z)%x,z);
    spfa(1%x);
    for (int i=0;i<x;i++) if (dis[i]!=-1&&h-dis[i]>=0) ans+=(h-dis[i])/x+1;
    printf("%lld",ans);
}