1.二叉搜索树(BST,Binary Search Tree)
顺序性:对于任意节点r,其左子树中的所有节点均<=r,其右子树的所有节点均>=r。
单调性:BST的中序遍历序列为单调递增序列。

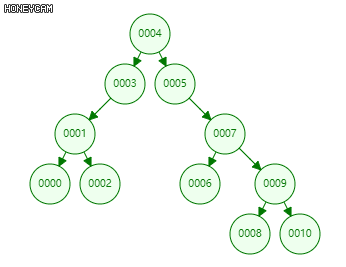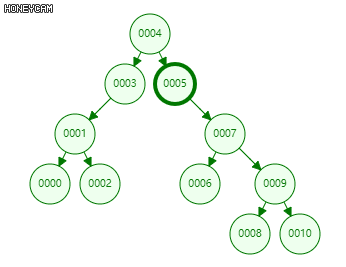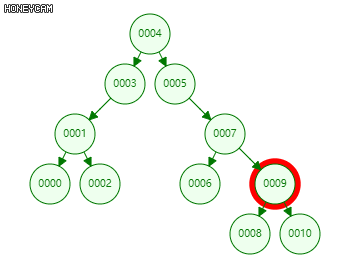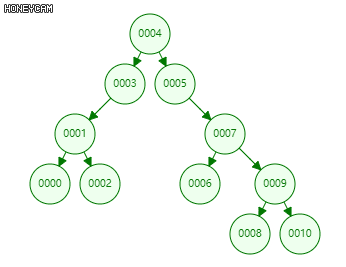
↑BST中的节点与中序编列中的节点一一对应,上下对齐
查找算法:类似二分查找,比较大小,定位节点。
1 template <typename T> //在以v为根的(AVL、SPLAY、rbTree等)BST子树中查找关键码e 2 static BinNodePosi(T) & searchIn ( BinNodePosi(T) & v, const T& e, BinNodePosi(T) & hot ) { 3 if ( !v || ( e == v->data ) ) return v; //递归基:在节点v(或假想的通配节点)处命中 4 hot = v; //一般情况:先记下当前节点,然后再 5 return searchIn ( ( ( e < v->data ) ? v->lc : v->rc ), e, hot ); //深入一层,递归查找 6 } //返回时,返回值指向命中节点(或假想的通配哨兵),hot指向其父亲(退化时为初始值NULL)
查找失败时返回空指针。
查找效率:最好O(1),最坏O(n):BST退化为线性链表。取决于树高。
插入算法:使用search定位要插入的节点应该插入的位置。
插入的节点一定为叶节点,插入效率同查找效率。
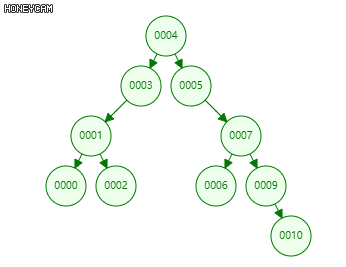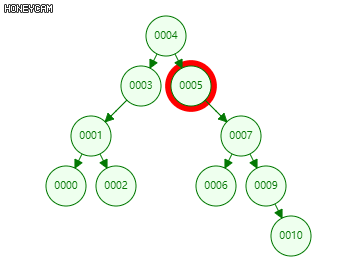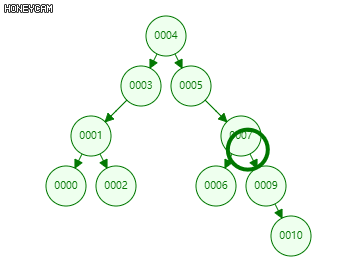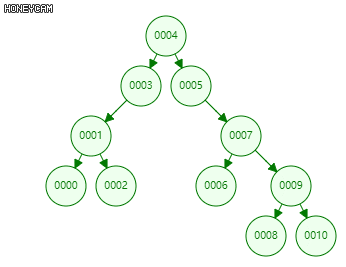
删除算法:根据目标节点的子节点个数可分为单分支和双分支两种情况。
单分支:即目标节点只有一个孩子(或没有孩子)。
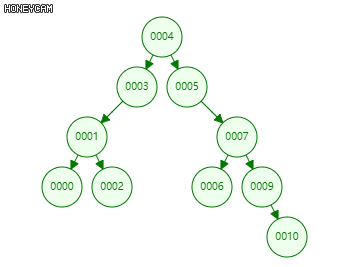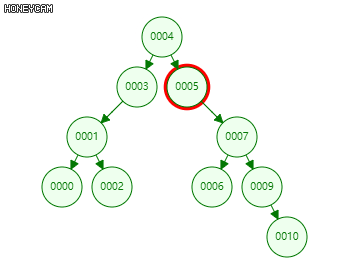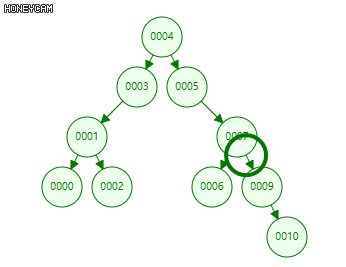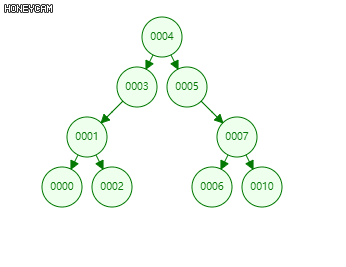
只需将目标节点与其左(右)子节点交换,删除子节点即可。
双分支:即目标节点有两个孩子。

找出该节点在中序遍历中的直接前驱(后继),交换两者位置,转换为单分支的情况。
事实上,考察中序遍历直接前驱/后继的定义可知,任意节点的直接前驱必无右子节点,直接后继必无左子节点。
1 template <typename T> 2 static BinNodePosi(T) removeAt ( BinNodePosi(T) & x, BinNodePosi(T) & hot ) { 3 BinNodePosi(T) w = x; //实际被摘除的节点,初值同x 4 BinNodePosi(T) succ = NULL; //实际被删除节点的接替者 5 if ( !HasLChild ( *x ) ) //若*x的左子树为空,则可 6 succ = x = x->rc; //直接将*x替换为其右子树 7 else if ( !HasRChild ( *x ) ) //若右子树为空,则可 8 succ = x = x->lc; //对称地处理——注意:此时succ != NULL 9 else { //若左右子树均存在,则选择x的直接后继作为实际被摘除节点,为此需要 10 w = w->succ(); //(在右子树中)找到*x的直接后继*w 11 swap ( x->data, w->data ); //交换*x和*w的数据元素 12 BinNodePosi(T) u = w->parent; 13 ( ( u == x ) ? u->rc : u->lc ) = succ = w->rc; //隔离节点*w 14 } 15 hot = w->parent; //记录实际被删除节点的父亲 16 if ( succ ) succ->parent = hot; //并将被删除节点的接替者与hot相联 17 release ( w->data ); release ( w ); return succ; //释放被摘除节点,返回接替者 18 }
2.平衡二叉搜索树(BBST,Balanced Binary Search Tree)
BST退化至链表,查找效率为O(n)

不难看出,其查找效率变成趋向O(n)的根本原因是树太高,导致根本没有发挥出二叉搜索树顺序性的优势。
因此,将二叉搜索树树的树高限制在一定的范围,就是提高查找效率的关键。
平衡二叉树:对于有n个节点的二叉树,树高恰好为log2n
如果使二叉搜索树同时具有了平衡性,其树高无疑会降到最低,维护二叉树顺序性、减治策略的优势也将发挥到最大。
平衡二叉搜索树包括AVL树,伸展树,红黑树等等...
理想平衡与适度平衡:理想平衡二叉树的高恰好为log2n,如完全二叉树。完全二叉树非常难得,所以理想平衡并不现实。
维持平衡的方法:旋转二叉树,zig和zag
zig:顺时针旋转
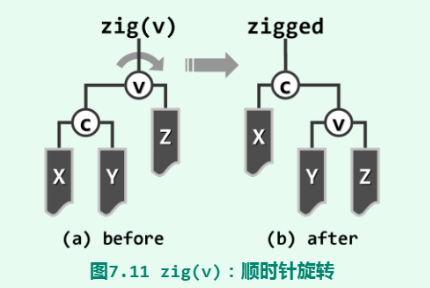
zag:逆时针旋转

通过旋转恢复平衡的条件是旋转前后的二叉树等价,即中序遍历序列不变。
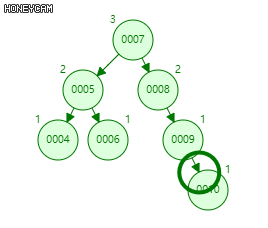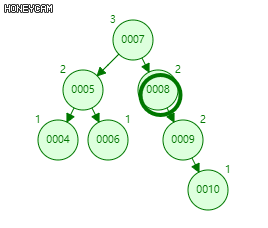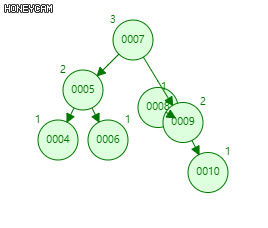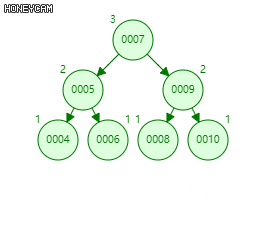
↑zag
旋转操作只涉及有限个节点,可在常数时间内完成。
3.AVL树
AVL树中任何节点的两个子树的高度差的绝对值<=1
平衡因子:任意节点的平衡因子=左子树高-右子树高
空树高度为-1,单节点高度取0,完全二叉树必是AVL树。
数学归纳法证明AVL的平衡性,略。
失衡与重平衡:对于一棵AVL树,尽管现在是平衡的,但经过插入和删除等操作后可能会失衡,这时候就需要重平衡。
失衡节点集:失衡后所有不再满足平衡因子绝对值<=1的节点的集合。
插入算法:插入引起的失衡,其失衡节点集中的节点都是新插入节点的祖先。
恢复平衡:单旋和双旋
单旋(zag)
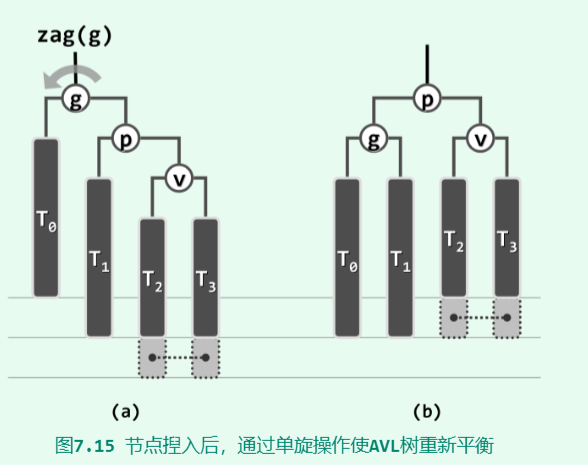
如果新节点的父节点只有一侧有其他失衡节点,可用zig/zag恢复平衡。
另一个镜像的情况使用zig,图为zag。
双旋(zig-zag)
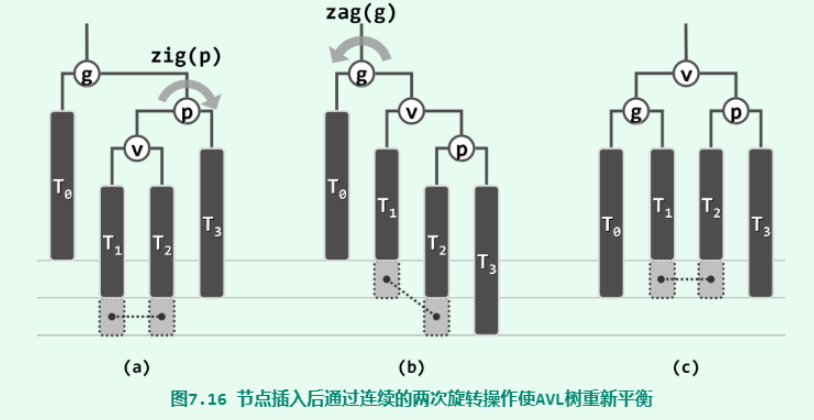
如果新节点的父节点两侧都有失衡节点,双旋。
不难发现,一次旋转之后,二叉树就已经转换成了单旋的情况。
镜像的情况可以用zag-zig处理。
插入而导致的失衡很好处理,因为只要最深的失衡节点完成了重平衡,其所有的祖先也都相应地完成了重平衡。
因此,插入操作最多只需两次旋转即可让整棵树恢复平衡。
1 template <typename T> BinNodePosi(T) AVL<T>::insert ( const T& e ) { //将关键码e插入AVL树中 2 BinNodePosi(T) & x = search ( e ); if ( x ) return x; //确认目标节点不存在 3 BinNodePosi(T) xx = x = new BinNode<T> ( e, _hot ); _size++; //创建新节点x 4 // 此时,x的父亲_hot若增高,则其祖父有可能失衡 5 for ( BinNodePosi(T) g = _hot; g; g = g->parent ) { //从x之父出发向上,逐层检查各代祖先g 6 if ( !AvlBalanced ( *g ) ) { //一旦发现g失衡,则(采用“3 + 4”算法)使之复衡,并将子树 7 FromParentTo ( *g ) = rotateAt ( tallerChild ( tallerChild ( g ) ) ); //重新接入原树 8 break; //g复衡后,局部子树高度必然复原;其祖先亦必如此,故调整随即结束 9 } else //否则(g依然平衡),只需简单地 10 updateHeight ( g ); //更新其高度(注意:即便g未失衡,高度亦可能增加) 11 } //至多只需一次调整;若果真做过调整,则全树高度必然复原 12 return xx; //返回新节点位置 13 } //无论e是否存在于原树中,总有AVL::insert(e)->data == e
插入效率=搜索效率=O(logn),重平衡为常数时间。
删除算法:失衡节点集中始终只有一个节点,可能是新节点的父节点。
重平衡的方法同样是单旋和双旋,不再重复。
4.3+4重构
单旋双旋左旋右旋实在过于复杂,且不同情况需要不同的处理,不如确定一个统一的重平衡方法,直接重构。
将失衡区域分解为3个节点、4个子树,保持中序遍历的序列不变,确保AVL的平衡性要求,重新组装出一棵新的树。
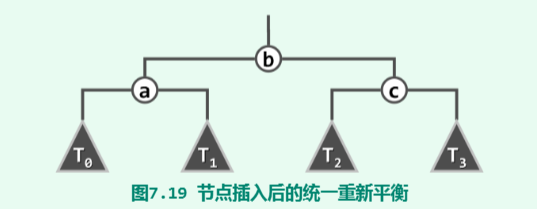
如上图所示,不妨将涉及到的节点、子树分别命名为abc,T0~T3
基于此实现concat34算法
1 template <typename T> BinNodePosi(T) BST<T>::connect34 ( 2 BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c, 3 BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3 4 ) { 5 //*DSA*/print(a); print(b); print(c); printf(" "); 6 a->lc = T0; if ( T0 ) T0->parent = a; 7 a->rc = T1; if ( T1 ) T1->parent = a; updateHeight ( a ); 8 c->lc = T2; if ( T2 ) T2->parent = c; 9 c->rc = T3; if ( T3 ) T3->parent = c; updateHeight ( c ); 10 b->lc = a; a->parent = b; 11 b->rc = c; c->parent = b; updateHeight ( b ); 12 return b; //该子树新的根节点 13 }
落实到具体的AVL树时,需要判别a,b,c以及T0~T3分别对应哪些实际的节点。
1 template <typename T> BinNodePosi(T) BST<T>::rotateAt ( BinNodePosi(T) v ) { //v为非空孙辈节点 2 /*DSA*/if ( !v ) { printf ( "a Fail to rotate a null node " ); exit ( -1 ); } 3 BinNodePosi(T) p = v->parent; BinNodePosi(T) g = p->parent; //视v、p和g相对位置分四种情况 4 if ( IsLChild ( *p ) ) /* zig */ 5 if ( IsLChild ( *v ) ) { /* zig-zig */ //*DSA*/printf(" zIg-zIg: "); 6 p->parent = g->parent; //向上联接 7 return connect34 ( v, p, g, v->lc, v->rc, p->rc, g->rc ); 8 } else { /* zig-zag */ //*DSA*/printf(" zIg-zAg: "); 9 v->parent = g->parent; //向上联接 10 return connect34 ( p, v, g, p->lc, v->lc, v->rc, g->rc ); 11 } 12 else /* zag */ 13 if ( IsRChild ( *v ) ) { /* zag-zag */ //*DSA*/printf(" zAg-zAg: "); 14 p->parent = g->parent; //向上联接 15 return connect34 ( g, p, v, g->lc, p->lc, v->lc, v->rc ); 16 } else { /* zag-zig */ //*DSA*/printf(" zAg-zIg: "); 17 v->parent = g->parent; //向上联接 18 return connect34 ( g, v, p, g->lc, v->lc, v->rc, p->rc ); 19 } 20 }
参考资料【1】《数据结构(C++语言版)》 邓俊辉