题目定义:
给定一个二维矩阵,计算其子矩形范围内元素的总和,该子矩阵的左上角为 (row1, col1) ,右下角为 (row2, col2) 。
上图子矩阵左上角 (row1, col1) = (2, 1) ,右下角(row2, col2) = (4, 3),该子矩形内元素的总和为 8。
示例:
给定 matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
题目解析:
首先使用 暴力破解 直接求该区域的解,时间复杂度为O(n * m) n为矩阵的行,m为矩阵的列
方式一(暴力破解):
class NumMatrix {
private int[][] matrix;
public NumMatrix(int[][] matrix) {
this.matrix = matrix;
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int result = 0;
for(int i = row1; i <= row2; i++){
for(int j = col1; j <= col2; j++){
result += matrix[i][j];
}
}
return result;
}
}
可以考虑使用前缀和,前缀和的意思是:假定给个一维数组是:[3, 0, 1, 4, 2], 那么从0开始统计该数组所有的前缀和为:[3,3,4,8,10],方式二在二维数组中统计所有的一维数据前缀和,然后进行累加,这样的时间复杂度缩减到了O(n)次
在实际的编码过程中,可以创建 matrix.length +1的数组,上述的前缀和变为:[0,3,3,4,8,10]这样就不用考虑初始值为0的情况了
方式二(一维前缀和):
class NumMatrix {
private int[][] sums;
public NumMatrix(int[][] matrix) {
if(matrix.length == 0 || matrix[0].length == 0)
return;
sums = new int[matrix.length][matrix[0].length + 1];
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix[0].length; j++)
sums[i][j + 1] = sums[i][j] + matrix[i][j];
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
int result = 0;
for(int i = row1; i <= row2; i++)
result +=(sums[i][col2 + 1] - sums[i][col1]);
return result;
}
}
再进行优化,可以直接统计二维数组的前缀和,这样每次查询,只需要一次就能得到结果,时间复杂度就降到了O(1)
其中,sums[i+1][j+1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];原理如下表:
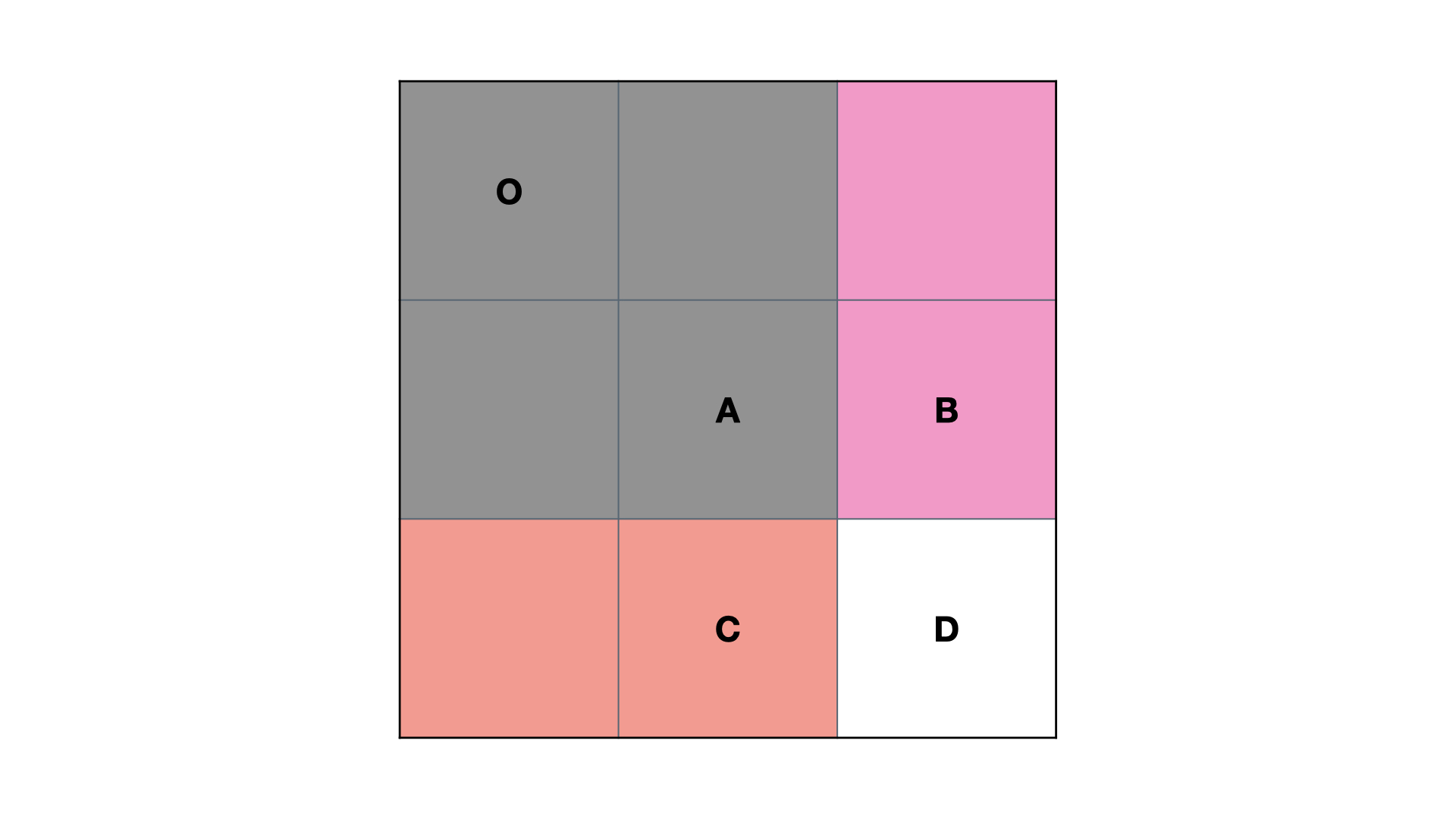
S(O,D)=S(O,C)+S(O,B)−S(O,A)+D
减去 S(O, A)S(O,A) 的原因是 S(O, C)S(O,C) 和 S(O, B)S(O,B) 中都有 S(O, A)S(O,A),即加了两次 S(O, A)S(O,A),所以需要减去一次 S(O, A)S(O,A)就得到了上述的公式。
求子矩阵的面试: sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1]
原理如下表:
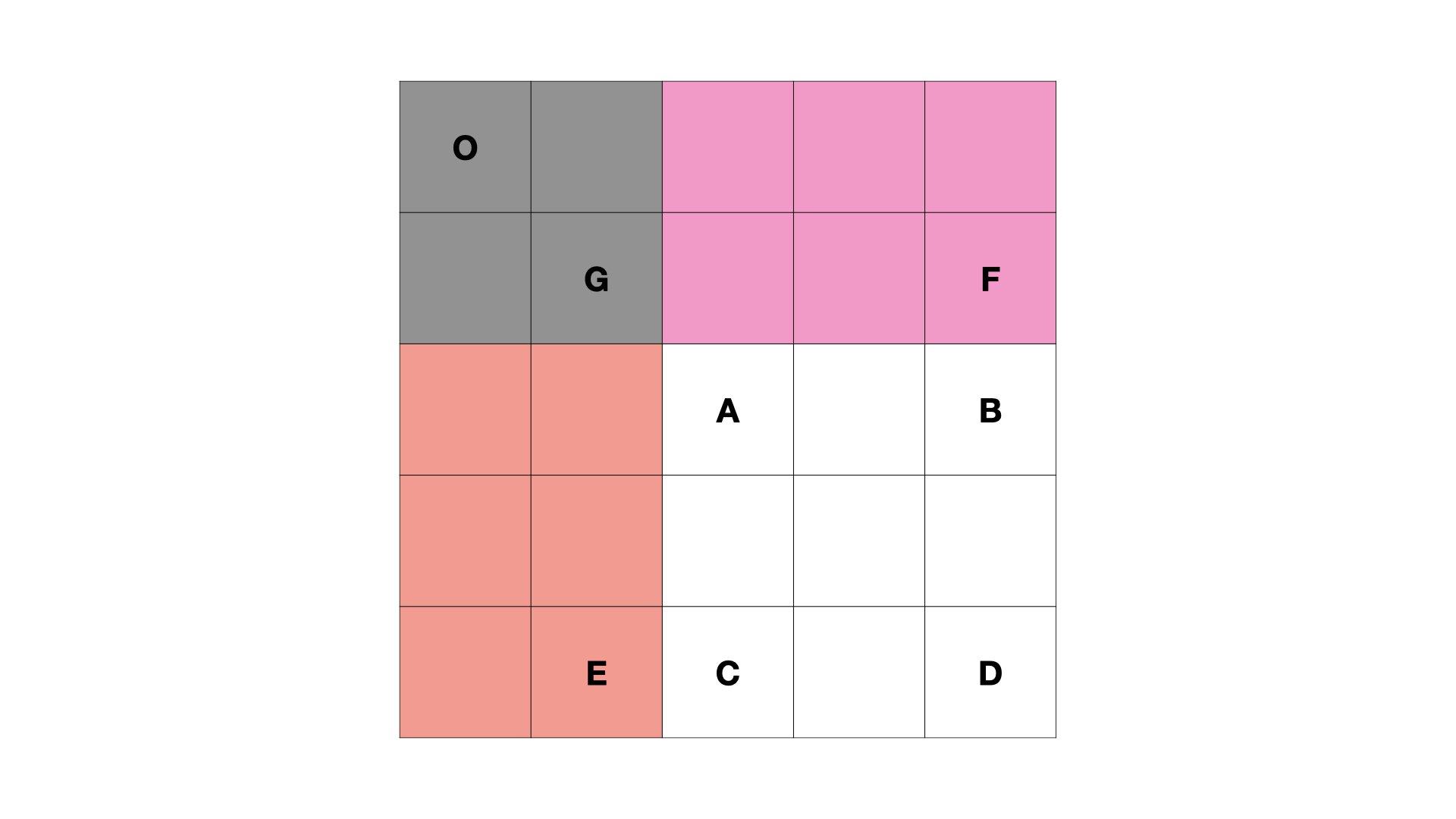
加上子矩形 S(O, G)S(O,G) 面积的原因是 S(O, E)S(O,E) 和 S(O, F)S(O,F) 中都有 S(O, G)S(O,G),即减了两次 S(O, G)S(O,G),所以需要加上一次 S(O, G)S(O,G),就得到了求子矩阵的公式
方式三(二维前缀和):
class NumMatrix {
private int[][] sums;
public NumMatrix(int[][] matrix) {
if(matrix.length == 0 || matrix[0].length == 0)
return;
sums = new int[matrix.length + 1][matrix[0].length + 1];
for(int i = 0; i < matrix.length; i++){
for(int j = 0; j < matrix[0].length; j++){
sums[i + 1][j + 1] = sums[i][j + 1] + sums[i + 1][j] - sums[i][j] + matrix[i][j];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return sums[row2 + 1][col2 + 1] - sums[row1][col2 + 1] - sums[row2 + 1][col1] + sums[row1][col1];
}
}