二叉树中序遍历的三种方式

leetcode(94 Binary Tree Inorder Traversal) 题目：

Given a binary tree, return the inorder traversal of its nodes' values.

Example:

Input:
   [1,null,2,3]
   1
    
     2
    /
   3
Output:   [1,3,2]

一棵树的中序遍历分为三步骤：

• 先遍历其左子树
• 再遍历本身节点
• 最后遍历其右子树

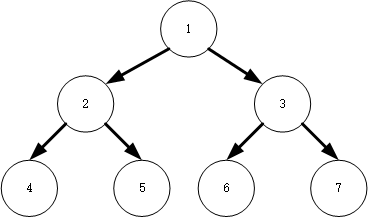
以下图为例，中序遍历的结果为 [4,2,5,1,6,3,7]

先定义树的结构：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

1.递归方式：

public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        helper(root,result);
        return result;
    }
    public void helper(TreeNode root,List<Integer> result){
        if(root != null){
            if(root.left != null)
                helper(root.left,result);
            result.add(root.val);
            if(root.right !=null)
                helper(root.right,result);
        }
    }

2.迭代方式：

 public List<Integer> inorderTraversal(TreeNode root) {
        if(root == null)
            return new ArrayList<Integer>();
        List<Integer> result = new ArrayList<>();
        Stack<TreeNode> stack = new Stack();
        TreeNode temp = root;
        while(temp !=null || !stack.isEmpty()){
            while(temp != null){
                stack.push(temp);
                temp =temp.left;
            }
            temp = stack.pop();
            result.add(temp.val);
            temp =temp.right;
        }
        return result;
    }

3.莫里斯遍历方式：

 public List<Integer> inorderTraversal(TreeNode root) {
        if(root == null)
            return new ArrayList<>();
        TreeNode cur = root;   //当前节点的位置
        List<Integer> res = new ArrayList<>();
        while(cur != null){
            if(cur.left ==null){
                res.add(cur.val);
                cur = cur.right;
            }else{
                TreeNode pre = cur.left;
                while(pre.right != null && pre.right !=cur){  //寻找左子树的最右节点
                    pre = pre.right;
                }
                if(pre.right == null){  //返回父结点
                    pre.right =cur;
                    cur = cur.left;
                }else{                  // 已遍历过，需要断开连接
                    pre.right = null;
                    res.add(cur.val);   //中序遍历存放当前节点
                    cur = cur.right;
                }
            }
        }
        return res;
    }

前两中方式代码一目了然，后一种方式需要稍稍阐述下原理与步骤：

原理：

​ 递归或者栈的空间复杂度都是O(n)，假设我们需要O(1)空间复杂度的遍历，是否有一种方式可以实现，答案是可以的。我们可以使用线索二叉树(threaded binary tree)的概念，利用叶子节点的空指针寻找其前序后继节点，左指针指向前驱节点，右指针指向后继节点，这样做到了O(n)时间复杂度，O(1)空间复杂度的遍历。

​

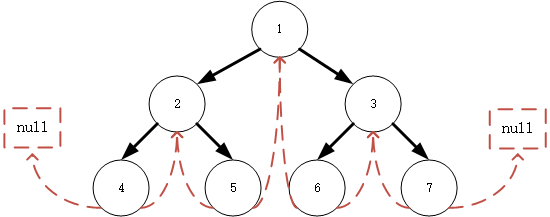
如上图所示，利用叶子节点的空指针指向其前序后继节点(红色标识)，假如我们想中序遍历，只需要先寻找出第一个左子树为null的节点，然后按照线索二叉树的线索进行判断是后继节点还是右子树，若是后继节点，则直接遍历(放入res中) 然后跳转到其右子树：

public List<Integer> threadedTreeListByInOrder() {
        HeroNode node = root;
     	List<Integer> res = new ArrayList<>();
        while (node != null) {
            while (node.getLeftType() == 0) {
                node = node.left;
            }
            res.add(node.val);
            while (node.getRightType() == 1) {
                node = node.right;
                res.add(node.val);
            }
            node = node.right;
        }
    	return res; 
    }

​ 但这里有一个限制(你在代码里也注意到了)，就是在定义树结构的时候，需要声明两个线索，用于判断其左指针是前驱节点还是左子树：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     int leftType;   //判断左指针的类别
 *     int rightType;  //判断右指针的类别
 *     TreeNode(int x) { val = x; }
 * }
 */

​ 这样本质上，就改变了树形结构的定义。那有没有一种既用了线索二叉树的原理，又不改变其定义呢？答案依然是有的，就是本文第三种遍历方式：Morris Traversal

​ Morris Traversal：通过动态创建线索的方法进行遍历，遍历某个节点完后，将该节点相关联的线索(姑且这么称呼吧)进行删除，遍历完后，不改变树的结构和原本的数据分布

实现原则分为2大步：首先记当前节点为cur

• 1：若cur的左子节点为null,遍历该节点，当前节点cur 指向其右子节点

• 2：若cur的左子节点不为null,设pre为 cur的左子节点，pre为一个临时节点 遍历寻找pre下的最右侧叶节点，并复制给pre [pre =pre.right]

  • 2.1：若pre的右子节点 为null, 将当前节点cur赋值给pre的右子节点[pre.right=cur]，cur 移到自身的的左子节点[cur = cur.left]
  • 2.2：若pre的右子节点为cur，表示pre到cur已经连接了，现在需要遍历然后结束该连接，所以，录入cur节点[res.add(cur.val)]，并将pre的右子节点置空[pre.right=null]，之后cur移到自身的右子节点[cur =cur.right]

  重复上述的2大步直到节点cur为空

  如果前面的原则你有点迷糊，不要紧，我们以上面的例子做个全过程，帮助理解下 ，其中res 存放遍历后的节点 ：

  

morris遍历过程：

• (1)：首先cur 从头节点 1 开始,按照前面morris原则的第二步，它存在左子节点，先搜寻左子节点的最右侧节点并赋值给pre，该节点为 5 ，再根据最右侧叶节点的值为null,所以将 5 的右子节点指向1，cur移动到自身的左子节点 2 res=[]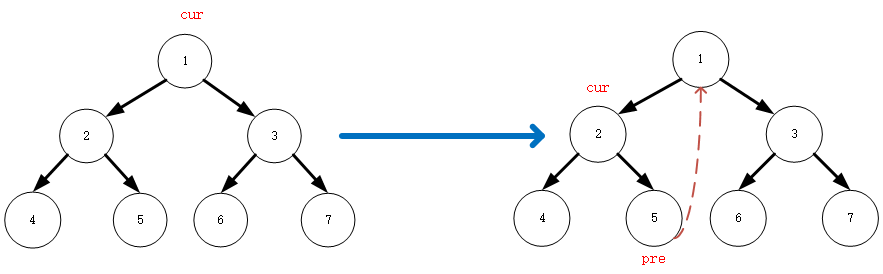

  

• (2)：2 有左子节点，且2的左子节点4 按照morris原则第二步，先搜寻左子节点的最右侧节点，根据最右侧叶节点的值为null,按照2.1原则，**所以将 4 的右子节点指针指向 2 ，cur移到自身的左子节点 4 res=[]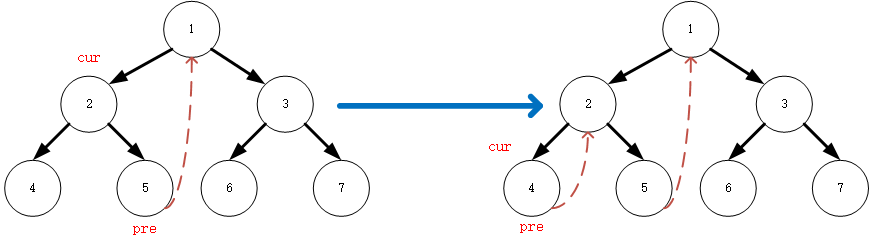

  

• (3)：4没有左子节点，按照morris原则第一步，遍历该节点并将cur指向该节点的右子节点 (在上一步中，我们已经将4的右指针指向了2，所以我们可以直接进行跳转至4的右子节点2) res=[4]

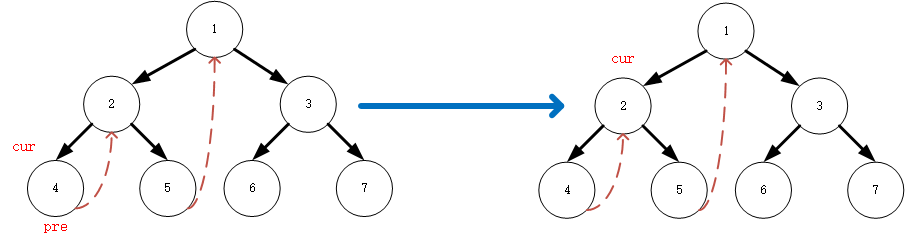
• (4)：cur此时回到了2, 2有左子节点，按照morris原则的第二步，搜寻左子节点的最右侧节点，发现在搜寻过程中4的右子节点指向了cur，按照前面的2.2原则，4的右指针指向null，遍历当前节点，同时cur指向其右子节点 5 res=[4,2]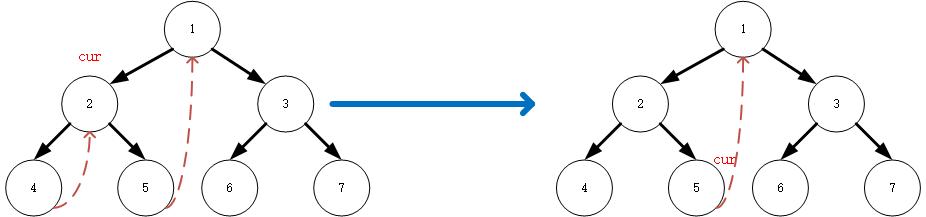

  

• (5)：5不存在右子节点，按照morris原则的第一步，遍历该节点并将cur指向该节点的右子节点(根据流程的第一步，我们已经将5节点的右指针指向了1，所以cur跳转至1) res=[4,2,5]

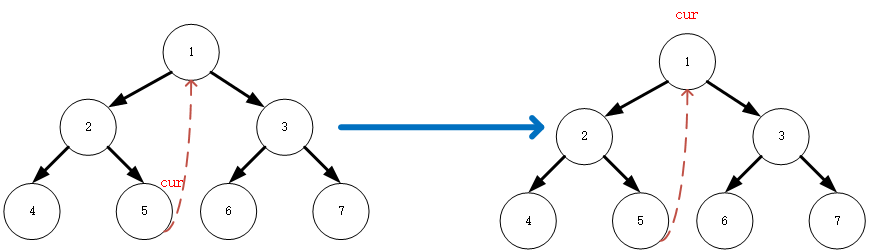
• (6)：cur此时回到了1，按照morris原则的第二步，搜寻左子节点的最右侧节点，发现在搜寻过程中5的右子节点指向了cur，按照前面的2.2原则，5的右指针指向null，遍历当前节点，同时cur指向其右子节点 3(这一步与流程的第4步一样) res=[4,2，5，1]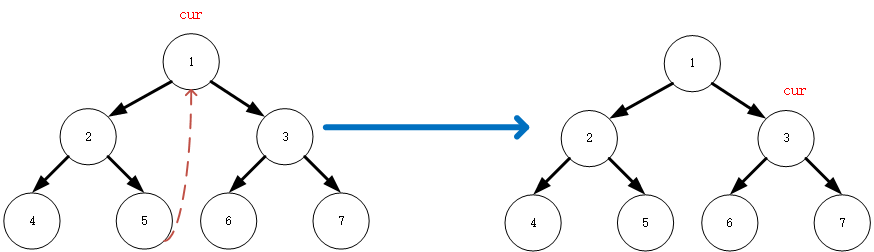

  

• (7)：3有左子节点7，按照morris原则第二步，先搜寻左子节点的最右侧节点，根据最右侧叶节点的值为null,按照2.1原则所以将 6 的右子节点指针指向 3 ，cur移到自身的左子节点 6 res=[4,2,5,1]

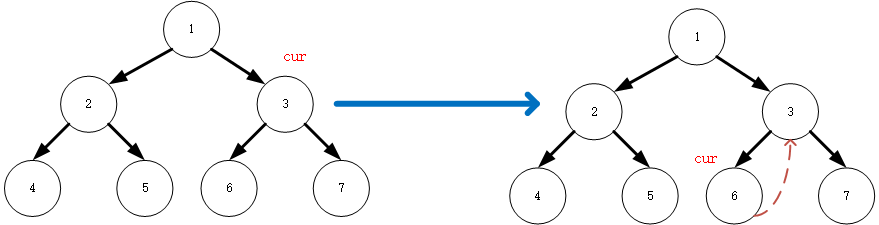
• (8)：6没有左子节点，按照morris原则的第一步，遍历该节点并将cur指向该节点的右子节点res=[4,2,5,1，6]

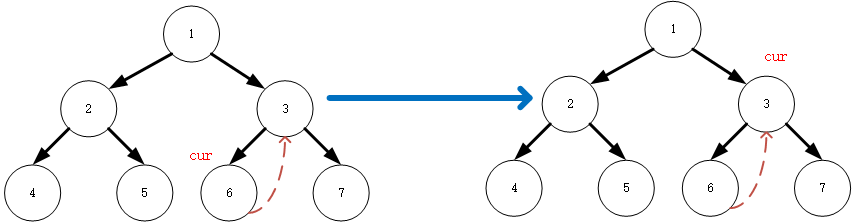
• (9)：cur此时回到了3，有左子节点6，依然是搜寻左子节点下的最右侧节点，搜寻过程中发现右侧节点指向cur本身，按照morris原则的2.2 ，6的右指针指向null，遍历当前节点，同时cur指向其右子节点 7 res=[4,2,5,1，6，3]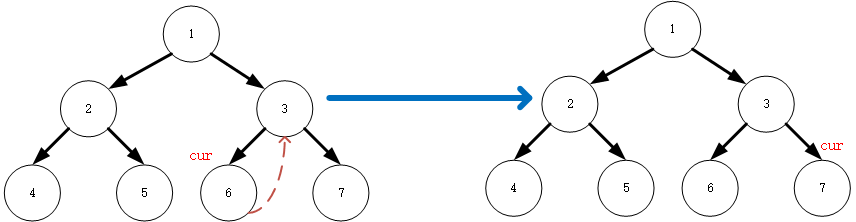

  

• (10) :7没有左子节点，直接遍历并将cur指向该节点的右子节点 ，最后cur指向了null,此时整个中序遍历完成。 res=[4,2,5,1，6，3,7]

​ 空间复杂度：O(1)，比较好推断

​ 时间复杂度：O(n)。可能会疑问以下代码跟树的高度有关：

 while(pre.right != null && pre.right !=cur)  //寻找左子树的最右节点
                    pre = pre.right;

但事实上，寻找所有节点的前驱节点只需要O(n)时间。以上面的流程为例，寻找前驱节点中所有的节点最多被访问了两遍！加上自身的遍历，总共最多访问3遍。所以，树的每个节点最多访问3遍，时间复杂度为O(n)。

参考：

Morris Traversal方法遍历二叉树（非递归，不用栈，O(1)空间）

神级遍历——morris

94. Binary Tree Inorder Traversal