代码:
class MaxHeap {
// 堆得存储结构:数组
private int[] data;
/**
* 构造方法:传入一个数组,并转换为一个最大堆
*
* @param data
*/
public MaxHeap(int[] data) {
this.data = data;
buildHeap();
}
/**
* 将数组转化为最大堆
*/
private void buildHeap() {
//完全二叉树只有数组下标小于或等于 (data.length) / 2 - 1 的元素有孩子结点,遍历这些结点。
//比如上面的图中,数组有10个元素, (data.length) / 2 - 1的值为4,a[4]有孩子结点,但a[5]没有
//即,从下自上开始堆化(从最下层非叶子节点开始)
for (int i = (data.length) / 2 - 1; i >= 0; i--) {
heapify(i);
}
}
/**
* 从当前节点开始堆化
*
* @param i
*/
private void heapify(int i) {
int biggest = i;
int r = right(i);
int l = left(i);
if (data[l] > data[r]) {
biggest = l;
} else {
biggest = r;
}
if (data[i] > data[biggest]) {
biggest = i;
}
if (biggest == i) return;
else {
swap(i, biggest);
//递归上升,升到该节点能升到的最高位置
heapify(biggest);
}
}
/**
* 获取右节点的数组下标
*
* @param i
* @return
*/
private int right(int i) {
//数组越界直接返回自己
if ((i + 1) << 1 >= data.length) return i;
//(i+1)*2
return (i + 1) << 1;
}
/**
* 获取左节点的数组下标
*
* @param i
* @return
*/
private int left(int i) {
//数组越界直接返回自己
if (((i + 1) << 1) - 1 >= data.length) return i;
return ((i + 1) << 1) - 1;
}
/**
* 交换元素位置
*
* @param i
* @param j
*/
private void swap(int i, int j) {
int tmp = data[i];
data[i] = data[j];
data[j] = tmp;
}
/**
* 获取堆中最大元素,即根元素
*
* @return
*/
public int getRoot() {
return data[0];
}
/**
* 替换根元素,并重新构建堆
*/
public void moveMaximumAndAdd(int n) {
data[0]=data[data.length - 1];
data[data.length - 1] = n;
buildHeap();
}
}
验证:
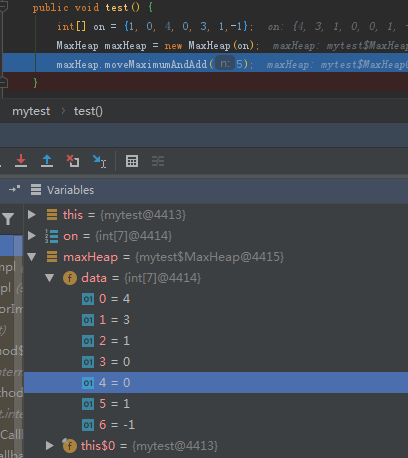
插入一个新值后:
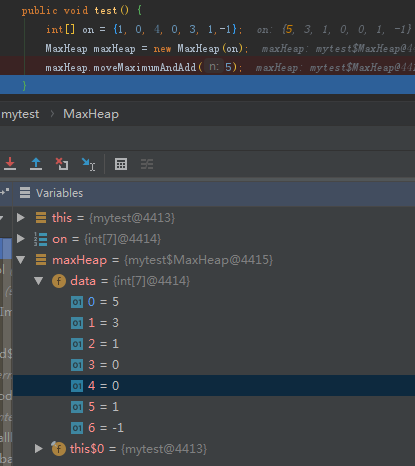
最关键的在于递归上升过程,只要大的升上去,小的值自然会被替换下沉下来