Big Number
| Time Limit: 1000MS | Memory Limit: 65536K |
Description
In many applications very large integers numbers are required. Some of these applications are using keys for secure transmission of data, encryption, etc. In this problem you are given a number, you have to determine the number of digits in the factorial of the number.
Input
Input consists of several lines of integer numbers. The first line contains an integer n, which is the number of cases to be tested, followed by n lines, one integer 1 <= m <= 10^7 on each line.
Output
The output contains the number of digits in the factorial of the integers appearing in the input.
Sample Input
2
10
20
Sample Output
7
19
【题目大意】
给出一个数字N,求N!的结果的位数.
【题目分析】
·直接暴力应该会超时
· 可以用Stirling(斯特林)公式。
· 可以打表,
【斯特林公式】
[摘自维基百科]

【求一个整数的位数】
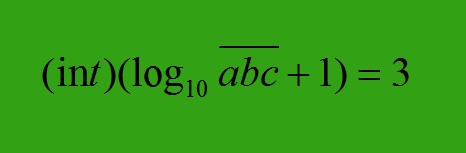
【求∏】
利用库函数<cmath>
∏ = acos(double(-1));
【参考代码】
1 /*============================================================================*\ 2 * POJ 1423 Big Number 3 * @author CocoonFan 4 * @date 3/3/2013 5 \*============================================================================*/ 6 7 #include <iostream> 8 #include <cmath> 9 10 using namespace std; 11 12 const double e = 2.718281828459045, pi = acos(double(-1)); 13 14 int num_of_digits(int n){//斯特林公式 15 if(n) 16 return (int)(log10(2*pi*n)/2.0+n*(log10(n/e)))+1; 17 else 18 return 1; 19 } 20 21 int main() 22 { 23 int t,n; 24 cin >> t; 25 while(t--&&cin >> n){ 26 cout << num_of_digits(n) << endl; 27 } 28 29 return 0; 30 }