国际惯例的题面: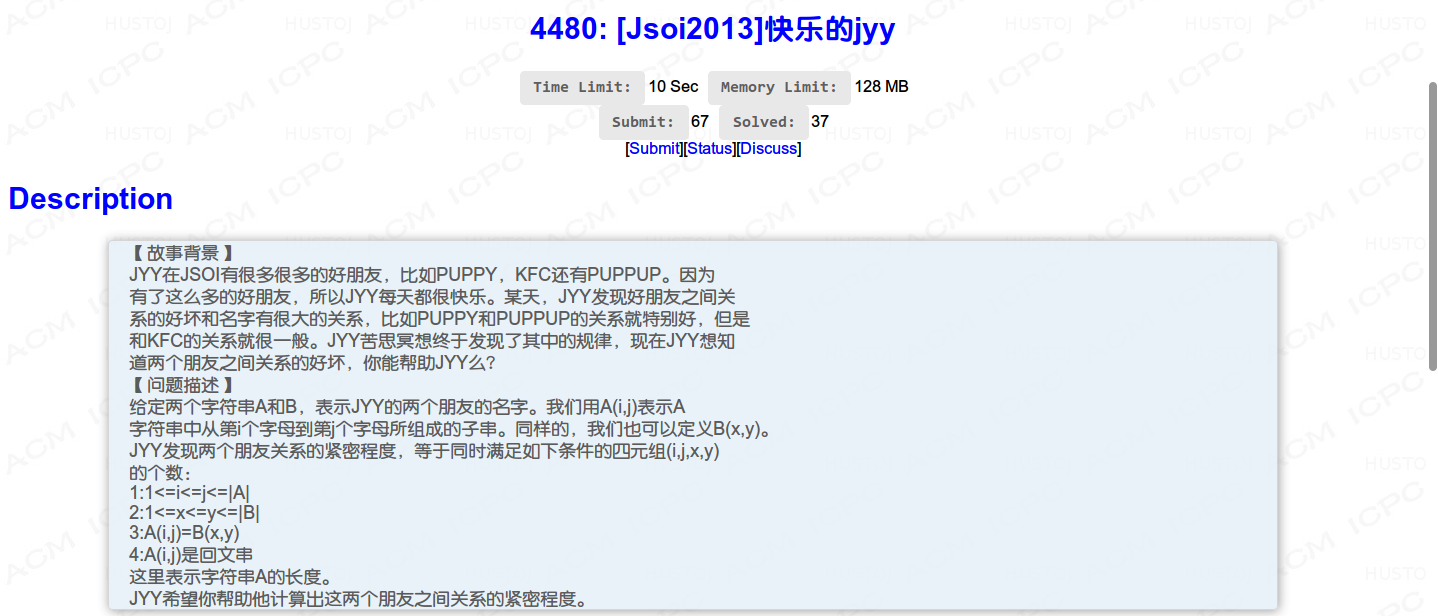
有人说这是回文自动机的板子题,然而我是不会这种东西的。
于是,我选择用更一般性的方法去解决这个题,就是那一堆东西了。
首先,我们把两个串同时插入一个广义SAM里,拓扑排序维护每个节点的parent树的子树中来自两个串的right集合的大小sizA和sizB。
同时倍增求出parent树上每个节点向上2^k层的父亲是哪个节点。
显然一个串本质不同的回文串数量是O(n)的(什么你不知道?manacher的复杂度怎么证的?),我们对A串做manacher,在暴力拓展的时候,去后缀自动机上倍增查询这个包含这个串的最浅的节点(显然这个节点的right集合最大),这个串对答案的贡献就是这个节点的sizA*sizB了。
为了防止同样的串被统计多次,我们需要哈希和unordered_set去重。
这个题的广义SAM在建立的时候,无论如何要新建节点,不能走已有的节点,否则会导致一些节点的len变小,出现一些不合法的情况。
总体时间复杂度O(nlogn),由于这种做法常数较大,所以BZOJ光荣垫底(然而AC这题还是绰绰有余的)。
代码:

1 #include<cstdio> 2 #include<cstring> 3 #include<algorithm> 4 #include<queue> 5 #include<tr1/unordered_set> 6 #define debug cout 7 typedef long long int lli; 8 typedef unsigned long long int ulli; 9 using namespace std; 10 using namespace tr1; 11 const int maxn=5e4+1e2,maxl=20; 12 const ulli base = 29; 13 14 char a[maxn],b[maxn]; 15 int la,lb; 16 int rec[maxn]; 17 lli ans; 18 19 struct ExtendedSuffixAutomatic { 20 int ch[maxn<<2][26],len[maxn<<2],fa[maxn<<2],anc[maxn<<2][maxl]; 21 int siz[maxn<<2][2],deg[maxn<<2],root,cnt; 22 inline int NewNode(int ll) { 23 return len[++cnt] = ll , cnt; 24 } 25 ExtendedSuffixAutomatic() { root = NewNode(0); } 26 inline void extend(int x,int p) { 27 int np = NewNode(len[p]+1); 28 while( p && !ch[p][x] ) ch[p][x] = np , p = fa[p]; 29 if( !p ) fa[np] = root; 30 else { 31 int q = ch[p][x]; 32 if( len[q] == len[p] + 1 ) fa[np] = q; 33 else { 34 int nq = NewNode(len[p]+1); 35 memcpy(ch[nq],ch[q],sizeof(ch[q])) , fa[nq] = fa[q]; 36 fa[np] = fa[q] = nq; 37 while( p && ch[p][x] == q ) ch[p][x] = nq , p = fa[p]; 38 } 39 } 40 } 41 inline void Ex_extend(char* s,int li,int bel) { 42 int cur = root; 43 for(int i=1;i<=li;i++) { 44 extend(s[i]-'A',cur) , cur = ch[cur][(int)s[i]-'A']; // a's A is different with b's A . 45 ++siz[cur][bel]; 46 if( !bel ) rec[i] = cur; 47 } 48 } 49 inline void topo() { 50 for(int i=1;i<=cnt;i++) if( fa[i] ) ++deg[fa[i]]; 51 queue<int> q; 52 for(int i=1;i<=cnt;i++) if( !deg[i] ) q.push(i); 53 while( q.size() ) { 54 const int pos = q.front(); q.pop(); 55 if( pos == root ) break; 56 anc[pos][0] = fa[pos]; 57 for(int i=0;i<2;i++) siz[fa[pos]][i] += siz[pos][i]; 58 if( !--deg[fa[pos]] ) q.push(fa[pos]); 59 } 60 for(int j=1;j<20;j++) for(int i=1;i<=cnt;i++) anc[i][j] = anc[anc[i][j-1]][j-1]; 61 } 62 inline lli query(int pos,int lim) { 63 for(int j=19;~j;j--) if( len[anc[pos][j]] >= lim ) pos = anc[pos][j]; 64 return (lli) siz[pos][0] * siz[pos][1]; 65 } 66 }esam; 67 68 struct Hash { 69 ulli pows[maxn],h[maxn]; 70 inline void build(char* s,int li) { 71 *pows = 1; 72 for(int i=1;i<=li;i++) pows[i] = pows[i-1] * base , h[i] = h[i-1] * base + s[i] - 'A' + 1; 73 } 74 inline ulli query(int l,int r) { 75 return h[r] - h[l-1] * pows[r-l+1]; 76 } 77 }hsh; 78 79 unordered_set<ulli> vis; 80 81 inline void calc(int al,int ar) { 82 ulli h = hsh.query(al,ar); 83 if( vis.find(h) != vis.end() ) return; 84 vis.insert(h) , ans += esam.query(rec[ar],ar-al+1); 85 } 86 87 inline void manacher(char* s,int li) { 88 static char in[maxn<<1]; 89 static int f[maxn<<1],app[maxn<<1],len,pos,mxr; 90 #define getpos_l(i) (app[i]|app[i+1]) 91 #define getpos_r(i) (app[i]|app[i-1]) 92 *in = '$'; 93 for(int i=1;i<=li;i++) in[++len] = s[i] , app[len] = i , in[++len] = '#'; 94 for(int i=1;i<=len;i++) { 95 if( i < mxr ) f[i] = min( f[pos*2-i] , mxr - i ); 96 else f[i] = 1; 97 if( i & 1 ) calc(getpos_l(i-f[i]+1),getpos_r(i+f[i]-1)); 98 while( in[i-f[i]] == in[i+f[i]] ) { 99 ++f[i]; 100 calc(getpos_l(i-f[i]+1),getpos_r(i+f[i]-1)); 101 } 102 if( i + f[i] > mxr ) mxr = i + f[i] , pos = i; 103 } 104 #undef getpos_l 105 #undef getpos_r 106 } 107 108 int main() { 109 scanf("%s%s",a+1,b+1) , la = strlen(a+1) , lb = strlen(b+1); 110 esam.Ex_extend(a,la,0) , esam.Ex_extend(b,lb,1) , esam.topo() , hsh.build(a,la); 111 manacher(a,la) , printf("%lld ",ans); 112 return 0; 113 }
この校舎がつくる影
教学楼所组成的影子
待ち合わせした音楽室
在音乐教室中等候
屋上から見えた 流れてくひこうき雲
从屋顶上看到的划过天际的飞行云
まだ残ってる落書き
还残留着的涂鸦
この瞳に映るすべて
映入眼帘的一切
伝えたい ひとつひとつに
想要传达 一个一个
想い出溢れること
满溢的思念
部室の窓から探してた
从活动室窗户寻找
遠くても君なら すぐにみつけられる
即使多么遥远你也立刻找出
