20180618小测

为什么今天还考试啊......

T1:

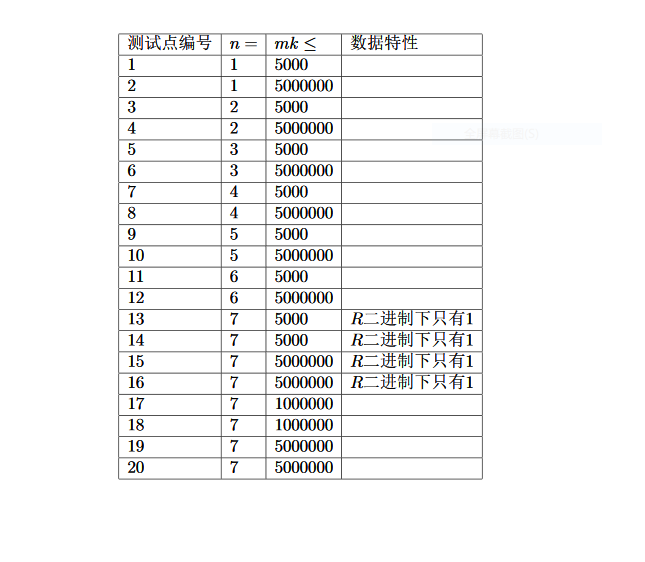
一眼不可做。
想维护分组状态，用最小表示法，总共8个集合，状态量400+，不可做。
弃疗写了20分的puts。
正解是容斥。
我们设f[i][j][k]为考虑i位，j个串，k个与输入串的前缀不完全相同，xor为0，数字可重复，考虑顺序的方案数，显然我们能把它扔进一个n*n的矩阵里转移。
然后我们令g[i]为考虑输入串全部，i个串，xor为0，数字不可重复，不考虑顺序的方案数。显然不考虑顺序不好做，我们先计算考虑顺序的，最后再除以阶乘。
考虑顺序的怎么算？我们考虑容斥。假设g[0,i-1]已经求出。我们考虑这i个串中有j个本质不同的串，显然j=i-2k，因为重复串必须出现两次。
然后我们枚举这i个串有多少出现在j个串中，多于剩下的串，假设有2p个，那么我们相当于是要在剩下的R-j个串中找p个可重复的串了。
怎么做？dfs一下，然后组合数+可重集排列就好。
然而细节还是不少的。
考场20分代码:

#include<cstdio>
using namespace std;

int main() {
    static int n;
    scanf("%d",&n);
    if( n <= 2 ) return printf("%d
",2-n) , 0;
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=8,maxm=5e6+1e2;
const int mod=1e9+7;

inline int add(const int &x,const int &y) {
    const int ret = x + y;
    return ret >= mod ? ret - mod : ret;
}
inline int sub(const int &x,const int &y) {
    const int ret = x - y;
    return ret < 0 ? ret + mod : ret;
}
inline int mul(const int &x,const int &y) {
    return (lli) x * y % mod;
}
inline void adde(int &dst,const int &x) {
    if( ( dst += x ) >= mod ) dst -= mod;
}
inline void sube(int &dst,const int &x) {
    if( ( dst -= x ) < 0 ) dst += mod;
}
inline void mule(int &dst,const int &x) {
    dst = (lli) dst * x % mod;
}
inline int fastpow(int base,int tim) {
    int ret = 1;
    while(tim) {
        if( tim & 1 ) mule(ret,base);
        if( tim >>= 1 ) mule(base,base);
    }
    return ret;
}

char in[maxm];
int n,m,k,t,R;
struct Matrix { // dat[1][i] means i number all same with R .
    int dat[maxn][maxn];
    Matrix(int tpe=0) {
        memset(dat,0,sizeof(dat));
        for(int i=0;i<=n;i++) dat[i][i] = tpe;
    }
    int* operator [] (const int &x) { return dat[x]; }
    const int* operator [] (const int &x) const { return dat[x]; }
    friend Matrix operator * (const Matrix &a,const Matrix &b) {
        Matrix ret;
        for(int i=0;i<=n;i++) for(int j=0;j<=n;j++) for(int k=0;k<=n;k++) adde(ret[i][j],mul(a[i][k],b[k][j]));
        return ret;
    }
    friend Matrix operator + (const Matrix &a,const Matrix &b) {
        Matrix ret;
        for(int i=0;i<=n;i++) for(int j=0;j<=n;j++) ret[i][j] = add(a[i][j],b[i][j]);
        return ret;
    }
}trans[maxn][2],f[maxn];
int g[maxn],fac[maxn],inv[maxn],lam[maxn][maxn],sel[maxn<<1];
int tab[1<<7];

inline int countbit(int x) {
    return tab[x];
}
inline int c(int n,int m) {
    return mul(fac[n],mul(inv[m],inv[n-m]));
}
inline void getrans(int n) {
    // get trans 0 .
    for(int same=0;same<=n;same++) {
        const int different = n - same;
        for(int different_select=0;different_select<=different;different_select++)
            if( ! ( different_select & 1 ) ) {
                adde(trans[n][0][same][same],c(different,different_select));
            }
    }
    // get trans 1 .
    for(int same=0;same<=n;same++) {
        const int different = n - same;
        for(int same_select=0;same_select<=same;same_select++)
            for(int different_select=0;different_select<=different;different_select++)
                if( ! ( ( same_select + different_select ) & 1 ) ) {
                    adde(trans[n][1][same][same_select],mul(c(same,same_select),c(different,different_select)));
                }
    }
}

inline Matrix fastpow(Matrix base,int tim) {
    Matrix ret(1);
    while(tim) {
        if( tim & 1 ) ret = ret * base;
        if( tim >>= 1 ) base = base * base;
    }
    return ret;
}
inline void getans() {
    for(int i=1;i<=n;i++) f[i][0][i] = 1;
    for(int j=1;j<=n;j++) {
        Matrix cur(1);
        for(int i=1;i<=t;i++) cur = cur * trans[j][(int)in[i]-'0'];
        f[j] = f[j] * fastpow(cur,m/t);
    }
    g[0] = 1;
    for(int i=1;i<=n;i++) g[i] = f[i][0][0];
    for(int i=1;i<=n;i++) if( ( i & 1 ) == ( n & 1 ) ) {
        for(int j=i&1;j<i;j+=2) sube(g[i],mul(g[j],lam[i][j]));
        mule(g[i],inv[i]);
    }
}

inline int getpir(int used,int ned) {
    int base = sub(R,used) , ret = 1;
    for(int i=1;i<=ned;i++) mule(ret,base) , sube(base,1);
    return mul(ret,inv[ned]);
}
inline void calc(int pos,int fs,int su) {
    if( pos < fs ) return;
    int ret = mul(getpir(fs,pos-fs-1),fac[su]);
    for(int i=1;i<pos;i++) mule(ret,inv[sel[i]]);
    adde(lam[su][fs],ret);
}
inline void dfs_lam(int pos,int rem,int fs,int su) {
    if(!rem) return calc(pos,fs,su);
    for(int i=1+(pos>fs);i<=rem;i+=2) sel[pos] = i , dfs_lam(pos+1,rem-i,fs,su);
}

inline void pre_lam() {
    *fac = 1;
    for(int i=1;i<=n;i++) fac[i] = mul(fac[i-1],i);
    inv[n] = fastpow(fac[n],mod-2);
    for(int i=n;i;i--) inv[i-1] = mul(inv[i],i);
    for(int i=1;i<=m;i++) adde(R,R) , adde(R,in[i]-'0');
    for(int i=1;i<=n;i++) if( ( i & 1 ) == ( n & 1 ) ) for(int j=i&1;j<i;j+=2) dfs_lam(1,i,j,i);
}

int main() {
    scanf("%d%d%s",&n,&k,in+1) , t = m = strlen(in+1);
    for(int i=1;i<1<<n;i++) tab[i] = tab[i>>1] + (i&1);
    for(int j=1;j<=m;j++) for(int i=1;i<k;i++) in[i*m+j] = in[j];
    m *= k , pre_lam();
    for(int i=1;i<=n;i++) if( ( i & 1 ) == ( n & 1 ) ) getrans(i);
    getans() , printf("%d
",g[n]);
    return 0;
}

T2:

40分暴力直接一个大力枚举+bitset即可。
正解的话，只需要考虑c=2或者c=3的情况，然后莫比乌斯反演。
咕咕咕了。
考场40分代码:

#include<cstdio>
#include<bitset>
#include<cmath>
typedef long long int lli;
using namespace std;
const int maxn=1e9+1e2;

bitset<maxn> vis;

inline int calc(int lim) {
    vis &= 0;
    for(int i=1;i<=1000;i++)
        for(int j=i+1,sq=sqrt(lim/i);j<=sq;j++)
            for(lli k=j*j;i*k<=lim;k*=j) vis[i*k] = 1;
    return vis.count();
}

int main() {
    static int l,r;
    scanf("%d%d",&l,&r) , printf("%d
",calc(r)-calc(l-1));
    return 0;
}

T3:

题意就是，我们求出每种点数的方案数，然后把它摊开，求方差。
只会20分dfs。
正解是一个O(n^4)的大力分类讨论+容斥+DP，具(我)体(也)做(是)法(抄)不(的)写(题)了(解)。
考场20分代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=(1<<20)+7,maxt=50;
const int mod=998244353;
const int dx[]={-1,1,0,0},dy[]={0,0,-1,1};

inline int sub(const int &a,const int &b) {
    const int ret = a - b;
    return ret < 0 ? ret + mod : ret;
}
inline int mul(const int &a,const int &b) {
    return (lli) a * b % mod;
}
inline void adde(int &dst,const int &x) {
    if( ( dst += x ) >= mod ) dst -= mod;
}
inline void mule(int &dst,const int &x) {
    dst = (lli) dst * x % mod;
}
inline int sq(const int &x) {
    return mul(x,x);
}

inline int fastpow(int base,int tim) {
    int ret = 1;
    while(tim) {
        if( tim & 1 ) mule(ret,base);
        if( tim >>= 1 ) mule(base,base);
    }
    return ret;
}

int vis[maxt][maxt];
int v[maxn],e[maxn],cnt;
int in[4],fs,n;

inline void dfs(int dep,int x,int y,int val,int ex) {
    if( dep > n ) {
        v[++cnt] = val , e[cnt] = ex;
        return;
    }
    ++vis[x][y];
    for(int i=0;i<4;i++) {
        const int tx = x + dx[i] , ty = y + dy[i];
        dfs(dep+1,tx,ty,val+!vis[tx][ty],mul(ex,in[i]));
    }
    --vis[x][y];
}

inline int calc() {
    int avr = 0 , su = 0 , ws = 0;
    for(int i=1;i<=cnt;i++) adde(avr,mul(v[i],e[i])) , adde(ws,e[i]);
    mule(avr,fastpow(ws,mod-2));
    for(int i=1;i<=cnt;i++) adde(su,mul(e[i],sq(sub(avr,v[i]))));
    return mul(su,fastpow(fs,n));
}

int main() {
    scanf("%d",&n);
    for(int i=0;i<4;i++) scanf("%d",in+i) , adde(fs,in[i]);
    dfs(1,n,n,1,1) , printf("%d
",calc());
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define Fixy for(int i=1;i<=n;i++) for(int x=-n;x<=n;x++) for(int y=-n;y<=n;y++)
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=2e2+1e1;
const int mod=998244353;
const int dx[]={-1,1,0,0},dy[]={0,0,-1,1};

inline int sub(const int &x,const int &y) {
    const int ret = x - y;
    return ret < 0 ? ret + mod : ret;
}
inline int mul(const int &x,const int &y) {
    return (lli) x * y % mod;
}
inline void adde(int &dst,const int &x) {
    if( ( dst += x ) >= mod ) dst -= mod;
}
inline void sube(int &dst,const int &x) {
    if( ( dst -= x ) < 0 ) dst += mod;
}
inline void mule(int &dst,const int &x) {
    dst = (lli) dst * x % mod;
}
inline int fastpow(int base,int tim) {
    int ret = 1;
    while(tim) {
        if( tim & 1 ) mule(ret,base);
        if( tim >>= 1 ) mule(base,base);
    }
    return ret;
}

int in[4],su,n;
int g[maxn],sumw[maxn],sumf[maxn];
struct Array {
    int dat[maxn>>1][maxn][maxn];
    inline int& operator () (const int &i,const int &x,const int &y) {
        return dat[i][x+n+1][y+n+1];
    }
}w,r,s,f;

inline int judge(const int &x,const int &y) {
    return -n <= x && x <= n && -n <= y && y <= n;
}
inline void getw() {
    w(0,0,0) = 1;
    for(int i=0;i<n;i++) for(int x=-n;x<=n;x++) for(int y=-n;y<=n;y++) if( w(i,x,y) ) for(int j=0;j<4;j++) {
        const int tx = x + dx[j] , ty = y + dy[j];
        if( judge(tx,ty) ) adde(w(i+1,tx,ty),mul(w(i,x,y),in[j]));
    }
}
inline void getg() {
    int pi = 1; g[0] = 1;
    for(int i=1;i<=n;i++) {
        mule(pi,su) , g[i] = pi;
        for(int j=1;j<=i;j++) sube(g[i],mul(w(j,0,0),g[i-j]));
    }
}
inline void getr() {
    Fixy {
        r(i,x,y) = w(i,x,y);
        for(int j=1;j<i;j++) sube(r(i,x,y),mul(w(j,0,0),r(i-j,x,y)));
    }
}
inline void gets() {
    Fixy {
        for(int j=1;j<i;j++) adde(s(i,x,y),mul(w(j,x,y),r(i-j,-x,-y)));
    }
}
inline void getf() {
    Fixy if( x || y ) {
        for(int j=1;j<=i;j++) adde(f(i,x,y),mul(g[i-j],w(j,x,y)));
        for(int j=1;j<=i;j++) sube(f(i,x,y),mul(g[i-j],s(j,x,y)));
        for(int j=1;j<=i;j++) sube(f(i,x,y),mul(f(i-j,x,y),sub(w(j,0,0),s(j,-x,-y))));
    }
}
inline int getans() {
    static int d,d2;
    for(int i=0;i<=n;i++) for(int x=-n;x<=n;x++) for(int y=-n;y<=n;y++) adde(sumf[i],f(i,x,y));
    for(int i=0;i<=n;i++) for(int x=-n;x<=n;x++) for(int y=-n;y<=n;y++) adde(sumw[i],w(i,x,y));
    for(int i=0;i<=n;i++) adde(d,mul(sumw[i],g[n-i]));
    for(int i=0;i<=n;i++) adde(d2,mul(sumf[i],sumw[n-i]));
    adde(d2,d2) , adde(d2,d) , mule(d2,fastpow(su,n));
    return sub(d2,mul(d,d));
}


int main() {
    scanf("%d",&n);
    for(int i=0;i<4;i++) scanf("%d",in+i) , adde(su,in[i]);
    getw() , getg() , getr() , gets() , getf() , printf("%d
",getans());
    return 0;
}

为什么这种容斥都不会啊......我菜爆了，还是退役吧！
对我而言的话，大概死亡也是一种救赎吧。(rm -rf ME)

冷た過ぎて 凍える夜も
在冷清凄惨之夜
もう 寂しくはないね
也不再感到寂寞
君といれたら 流れる星も
立于君旁 闪过的流星
綺麗に見えるんだ
看起来都那么绮丽
キラリ キラリ 瞬く星を
与你一起数过的
君と何度も数えたら
一闪一闪的漫天繁星
ひとつ ふたつ つながる絆
都结成我们的羁绊