三流选手拼知识,二流选手拼姿势,一流选手拼意识。
而我这种辣鸡选手,还是退役吧。
T1:
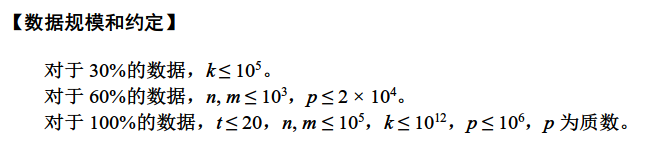
这题30分直接枚举建造多少个权值为2的,然后拓展lucas。
然后我就把这题当成51nod1538做,强行构造常系数线性递推,然后发现这不常系数不线性。
考虑下面怎么办,我们能手玩那个拓展lucas,然而这个人干事,且模数较小照样GG。
然后我想了一个O(knm)的dp,复杂度和模数无关,然而并没什么用。
正解是这样的,考虑我们把两个价值为1的绑定为一个价值为2的,这样的方案很好计算。
然后我们考虑价值为1且选择为奇数的有多少个,我们让选择奇数的减去多出的这个,剩下的一定是偶数,也很好计算。
于是两个组合数相乘即可,复杂度O(nlogPK)。
30分暴力代码:

1 #include<cstdio> 2 typedef long long int lli; 3 const int maxn=1e6+1e2; 4 5 lli fac[maxn],inv[maxn]; 6 int mod; 7 8 inline lli c(lli n,lli m) { 9 return fac[n] * inv[m] % mod * inv[n-m] % mod; 10 } 11 inline lli lucas(lli n,lli m) { 12 if( n < m ) return 0; 13 if( !m ) return 1; 14 if( n < mod && m < mod ) return c(n,m); 15 return lucas(n/mod,m/mod) * c(n%mod,m%mod) % mod; 16 } 17 18 inline lli fastpow(lli base,int tim) { 19 lli ret = 1; 20 while(tim) { 21 if( tim & 1 ) ret = ret * base % mod; 22 if( tim >>= 1 ) base = base * base % mod; 23 } 24 return ret; 25 } 26 27 inline void pre() { 28 *fac = 1; 29 for(int i=1;i<mod;i++) fac[i] = fac[i-1] * i % mod; 30 inv[mod-1] = fastpow(fac[mod-1],mod-2); 31 for(int i=mod-1;i;i--) inv[i-1] = inv[i] * i % mod; 32 } 33 34 int main() { 35 static int T; 36 static lli n,m,k,ans; 37 scanf("%d",&T); 38 while(T--) { 39 scanf("%lld%lld%lld%d",&n,&m,&k,&mod) , pre() , ans = 0; 40 if( !n && !m ) ans = !k; 41 else if( !n ) ans = ( k & 1 ) ? 0 : lucas((k>>1)+m-1,m-1); 42 else if( !m ) ans = lucas(k+n-1,n-1); 43 else for(lli i=0;i<=k>>1;i++) ans = ( ans + lucas(i+m-1,m-1) * lucas(k-(i<<1)+n-1,n-1) % mod ) % mod; 44 printf("%lld ",ans); 45 } 46 return 0; 47 }
正解代码:

1 #include<cstdio> 2 typedef long long int lli; 3 const int maxn=1e6+1e2; 4 5 lli fac[maxn],inv[maxn]; 6 int mod; 7 8 inline lli c(lli n,lli m) { 9 return fac[n] * inv[m] % mod * inv[n-m] % mod; 10 } 11 inline lli lucas(lli n,lli m) { 12 if( n < m ) return 0; 13 if( !m ) return 1; 14 if( n < mod && m < mod ) return c(n,m); 15 return lucas(n/mod,m/mod) * c(n%mod,m%mod) % mod; 16 } 17 18 inline lli fastpow(lli base,int tim) { 19 lli ret = 1; 20 while(tim) { 21 if( tim & 1 ) ret = ret * base % mod; 22 if( tim >>= 1 ) base = base * base % mod; 23 } 24 return ret; 25 } 26 27 inline void pre() { 28 *fac = 1; 29 for(int i=1;i<mod;i++) fac[i] = fac[i-1] * i % mod; 30 inv[mod-1] = fastpow(fac[mod-1],mod-2); 31 for(int i=mod-1;i;i--) inv[i-1] = inv[i] * i % mod; 32 } 33 34 int main() { 35 static int T; 36 static lli n,m,k,ans; 37 scanf("%d",&T); 38 while(T--) { 39 scanf("%lld%lld%lld%d",&n,&m,&k,&mod) , pre() , ans = 0; 40 for(int i=0;i<=n;i++) if( ! ( ( k - i ) & 1 ) ) ans = ( ans + lucas(n,i) * lucas(((k-i)>>1)+n+m-1,n+m-1) % mod ) % mod; 41 printf("%lld ",ans); 42 } 43 return 0; 44 }
T2:
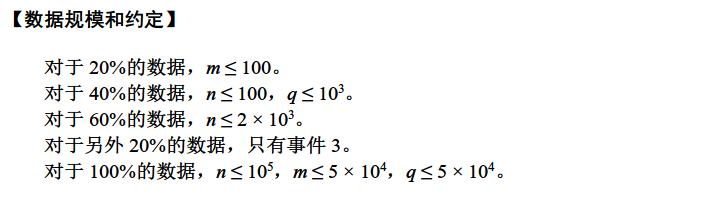
水题,我们把树变成dfs序列,显然我们能根据LCA位置分类讨论把两边能选择的跳跃点的出发点变成两个区间,然后就变成了一个单点加,矩形查询的二维数点问题。
然而内存没有开够512mb所以我树套树被卡成80,气。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cassert> 6 //#define debug cerr 7 //using namespace std; 8 const int maxn=1e5+1e2,maxe=3.5e7+1e2; 9 10 int n,m; 11 12 struct SegmentTree { 13 int lson[maxe],rson[maxe],sum[maxe],cnt; 14 inline void update(int &pos,int l,int r,const int &tar,const int &x) { 15 if( !pos ) { pos = ++cnt; } sum[pos] += x; 16 if( l == r ) return; 17 const int mid = ( l + r ) >> 1; 18 tar <= mid ? update(lson[pos],l,mid,tar,x) : update(rson[pos],mid+1,r,tar,x); 19 } 20 inline int query(int pos,int l,int r,const int &ll,const int &rr) { 21 if( !pos || ( ll <= l && r <= rr ) ) return sum[pos]; 22 const int mid = ( l + r ) >> 1; 23 if( rr <= mid ) return query(lson[pos],l,mid,ll,rr); 24 else if( ll > mid ) return query(rson[pos],mid+1,r,ll,rr); 25 return query(lson[pos],l,mid,ll,rr) + query(rson[pos],mid+1,r,ll,rr); 26 } 27 }sgt; 28 29 struct BinaryIndexTree { 30 int dat[maxn]; 31 #define lowbit(x) (x&-x) 32 inline void update(int x,const int &y,const int &val) { 33 while( x <= n ) sgt.update(dat[x],1,n,y,val) , x += lowbit(x); 34 } 35 inline int query(int x,const int &ll,const int &rr) { 36 int ret = 0; 37 while(x) ret += sgt.query(dat[x],1,n,ll,rr) , x -= lowbit(x); 38 return ret; 39 } 40 inline int query(int l,int r,const int &ll,const int &rr) { 41 return query(r,ll,rr) - query(l-1,ll,rr); 42 } 43 }bit; 44 45 int s[maxn],t[maxn<<1],nxt[maxn<<1]; 46 int dep[maxn],dfn[maxn],rit[maxn],anc[maxn][22]; 47 48 inline void addedge(int from,int to) { 49 static int cnt; 50 t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt; 51 } 52 inline void dfs(int pos,int fa) { 53 static int dd; 54 dfn[pos] = ++dd , *anc[pos] = fa; 55 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) dep[t[at]] = dep[pos] + 1 , dfs(t[at],pos); 56 rit[pos] = dd; 57 } 58 inline void pre() { 59 for(int j=1;j<22;j++) for(int i=1;i<=n;i++) anc[i][j] = anc[anc[i][j-1]][j-1]; 60 } 61 inline int lca(int x,int y) { 62 if( dep[x] < dep[y] ) std::swap(x,y); 63 for(int i=21;~i;i--) if( dep[x] - ( 1 << i ) >= dep[y] ) x = anc[x][i]; 64 if( x == y ) return x; 65 for(int i=21;~i;i--) if( anc[x][i] != anc[y][i] ) x = anc[x][i] , y = anc[y][i]; 66 return *anc[x]; 67 } 68 inline int nstson(int fa,int son) { 69 for(int i=21;~i;i--) if( dep[son] - ( 1 << i ) > dep[fa] ) son = anc[son][i]; 70 return son; 71 } 72 inline int query(int x,int y) { // assert x != y . 73 int lc = lca(x,y); 74 if( lc != x && lc != y ) return bit.query(dfn[x],rit[x],dfn[y],rit[y]); 75 else { 76 if( lc != x ) std::swap(x,y); 77 int ns = nstson(x,y); 78 return bit.query(1,n,dfn[y],rit[y]) - bit.query(dfn[ns],rit[ns],dfn[y],rit[y]); 79 } 80 } 81 82 int main() { 83 scanf("%d",&n); 84 for(int i=1,a,b;i<n;i++) scanf("%d%d",&a,&b) , addedge(a,b) , addedge(b,a); 85 dfs(1,-1) , scanf("%d",&m); 86 for(int i=1,a,b;i<=m;i++) scanf("%d%d",&a,&b) , bit.update(dfn[a],dfn[b],1) , bit.update(dfn[b],dfn[a],1); 87 scanf("%d",&m) , pre(); 88 for(int i=1,o,x,y;i<=m;i++) { 89 scanf("%d%d%d",&o,&x,&y); 90 if( o == 1 ) bit.update(dfn[x],dfn[y],1) , bit.update(dfn[y],dfn[x],1); 91 else if( o == 2 ) bit.update(dfn[x],dfn[y],-1) , bit.update(dfn[y],dfn[x],-1); 92 else if( o == 3 ) assert(x!=y) , printf("%d ",query(x,y)); // if x == y , it will be an undefined input data . 93 } 94 return 0; 95 }
T3:


这题根本没看......
现在也只改了tp=1的50分。
考虑我们重新定义权值为d/e,那么我们的答案就是选择部分的权值的连乘积乘以全部e的连乘积。
树形dp,考虑fi表示从i的子树选择一条链到叶子的权值的连乘积的和,gi表示从i的子树外面选一条链到叶子的权值的连乘积的和。
一个换根DP的转移,十分显然。
我们另ffi为fi*dis(fai,i),那么我们有一下公式:
(down=f,up=g,downfa=ff)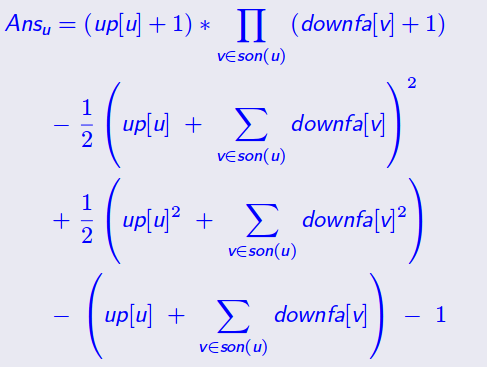
然后就能获得50分了。
代码:

1 #include<cstdio> 2 #include<cctype> 3 typedef unsigned int uint; 4 typedef unsigned long long int ulli; 5 const uint maxn=5e6+1e2; 6 7 uint s[maxn],t[maxn<<1],nxt[maxn<<1],l[maxn<<1]; 8 uint deg[maxn],f[maxn],g[maxn],pfs[maxn],as[maxn],assq[maxn]; 9 uint pi,ans,n,mod,inv,root; 10 11 inline uint add(const uint &a,const uint &b) { 12 uint ret = a + b; 13 return ret >= mod ? ret - mod : ret; 14 } 15 inline uint sub(const uint &a,const uint &b) { 16 return a >= b ? a - b : a + mod - b; 17 } 18 inline uint mul(const uint &a,const uint &b) { 19 return (ulli) a * b % mod; 20 } 21 inline void adde(uint &a,const uint &b) { 22 a = add(a,b); 23 } 24 inline void sube(uint &a,const uint &b) { 25 a = sub(a,b); 26 } 27 inline void mule(uint &a,const uint &b) { 28 a = (ulli) a * b % mod; 29 } 30 31 inline uint fastpow(uint base,uint tim) { 32 uint ret = 1; 33 while(tim) { 34 if( tim & 1 ) mule(ret,base); 35 if( tim >>= 1 ) base = mul(base,base); 36 } 37 return ret; 38 } 39 40 inline void addedge(uint from,uint to,uint len) { 41 static uint cnt; 42 t[++cnt] = to , l[cnt] = len , nxt[cnt] = s[from] , s[from] = cnt; 43 } 44 inline void dualedge(uint a,uint b,uint len) { 45 addedge(a,b,len) , addedge(b,a,len); 46 } 47 inline void dfs1(uint pos,uint fa) { 48 pfs[pos] = 1; 49 bool isleaf = 1; 50 for(uint at=s[pos],fs;at;at=nxt[at]) if( t[at] != fa ) { 51 isleaf = 0 , dfs1(t[at],pos) , fs = mul(f[t[at]],l[at]); 52 adde(f[pos],fs) , mule(pfs[pos],add(fs,1)) , adde(as[pos],fs) , adde(assq[pos],mul(fs,fs)); 53 } 54 adde(f[pos],isleaf); 55 } 56 inline void dfs2(uint pos,uint fa,uint lat) { 57 if( ~fa ) { 58 g[pos] = mul(add(g[fa],sub(f[fa],mul(f[pos],lat))),lat); 59 mule(pfs[pos],add(g[pos],1)) , adde(as[pos],g[pos]) , adde(assq[pos],mul(g[pos],g[pos])); 60 } 61 for(uint at=s[pos];at;at=nxt[at]) if( t[at] != fa ) dfs2(t[at],pos,l[at]); 62 } 63 inline void getans() { 64 for(uint i=1;i<=n;i++) { 65 if( deg[i] >= 3 ) adde(ans,sub(add(pfs[i],mul(assq[i],inv)),add(mul(mul(as[i],as[i]),inv),add(as[i],1)))); 66 } 67 } 68 69 70 namespace FastIO { 71 inline unsigned char nextchar() { 72 static const int BS = 1 << 22; 73 static unsigned char buf[BS],*st,*ed; 74 if( st == ed ) ed = buf + fread(st=buf,1,BS,stdin); 75 return st == ed ? 0 : *st++; 76 } 77 inline uint getint() { 78 uint ret = 0 , ch; 79 while( !isdigit(ch=nextchar()) ); 80 do ret = ret * 10 + ch - '0'; while( isdigit(ch=nextchar()) ); 81 return ret; 82 } 83 } 84 using FastIO::getint; 85 86 int main() { 87 if( getint() - 1 ) return 0; 88 n = getint() , mod = getint() , root = -1 , pi = 1 , inv = fastpow(2,mod-2); 89 for(uint i=1,a,b,d,e;i<n;i++) a = getint() , b = getint() , d = getint() , e = getint() , mule(pi,e) , dualedge(a,b,mul(d,fastpow(e,mod-2))) , ++deg[a] , ++deg[b]; 90 for(uint i=1;i<=n&&!~root;i++) if( deg[i] > 2 ) root = i; 91 if( !~root ) return puts("0"),0; 92 dfs1(root,-1) , dfs2(root,-1,0) , getans() , printf("%u ",mul(ans,pi)); 93 return 0; 94 }
曾经做到绝境翻盘,省二进队的创举的不是我,是神。现在的我只是一个菜鸡颓佬垃圾蒟蒻罢了。
可能上天就是想跟我开一个玩笑,告诉我看似美好的未来也会有无限的痛苦吧。
达成成就:连续四次考试没有rank1。
真的很不愿意活下去了呢。
崩れ去った 幻たち
那些虚幻 已崩塌瓦解
また始まりへと 旅をしてみたい
想要再次向开始的地方起程
悲しみをこめて誘うの
满含悲伤发出邀请
今ほんの少(すこ)し 夢うつつのはざま漂えたら
如今在狭窄的梦与现实的缝隙间飘摇
嗚呼わたしに 明日はいらない
啊 于我而言 没有明天
