2331: [SCOI2011]地板 插头DP

国际惯例的题面: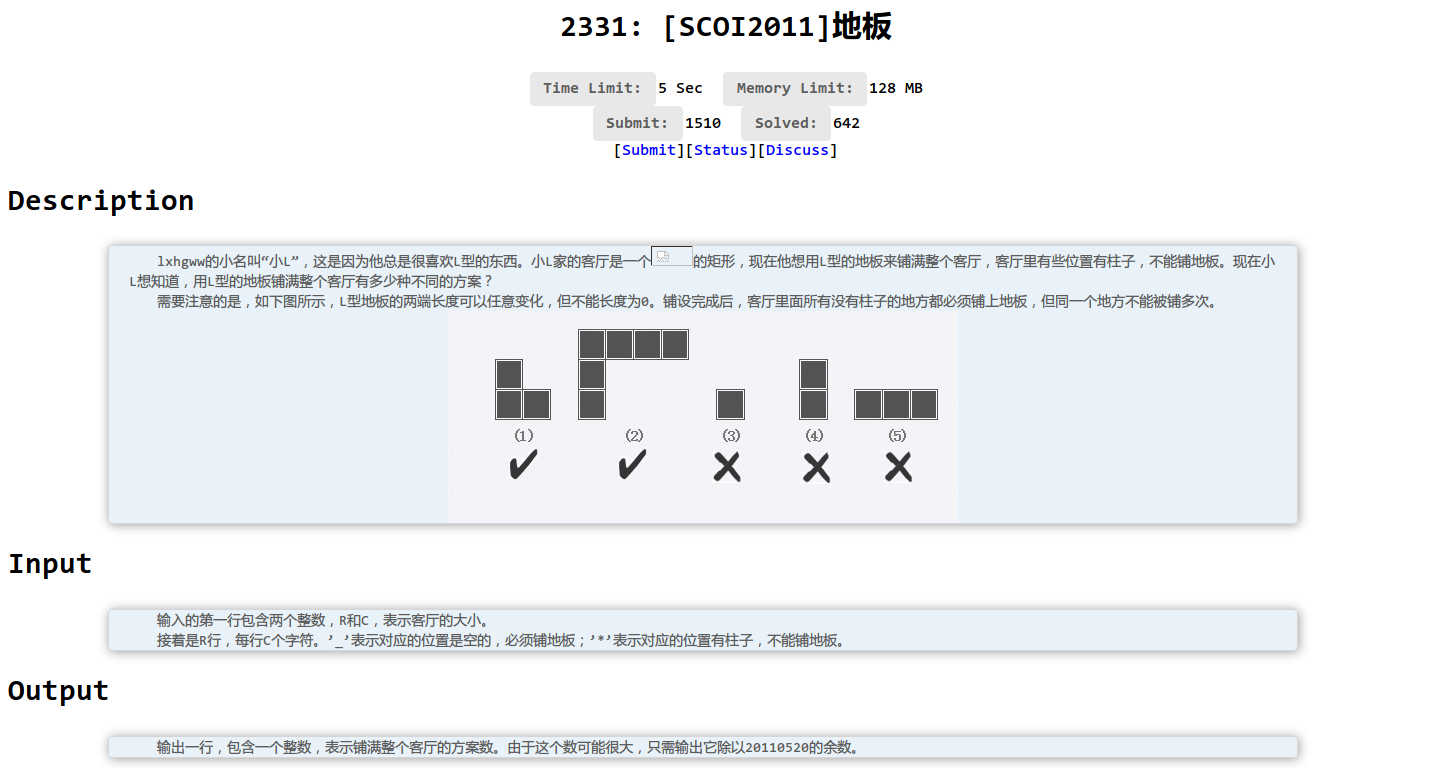

十分显然的插头DP。由于R*C<=100，所以min(R,C)<=10，然后就可以愉悦地状压啦。
我们用三进制状压，0表示没有插头，1表示有一个必须延伸至少一格且拐弯的插头，2表示有一个必须延伸一格且不可以拐弯的插头。
转移的话就十分显然了。
00->22，表示用这个格子作为开始的拐角。
00->10，表示用这个格子向下延伸。
00->01，表示用这个格子向右延伸。
01->10，表示这个格子连接上下。
01->02，表示在这个格子作为中间的拐角。
02->20，表示这个格子连接上下。
02->00，表示这个格子作为某个地板的终点。
10->01，表示这个格子连接左右。
10->20，表示在这个格子作为中间的拐角。
11->00，表示这个格子作为结束的拐角。
20->00，表示这个格子作为某个地板的终点。
20->02，表示这个格子连接左右。
(插头DP的本质就是分类讨论，所以麻烦也没办法，想明白就很容易了)
然后就是实现了。我是用unordered_map存储状态，同时先找到第一个可以放东西的位置开始DP，统计答案的时候统计第n+1行没有插头的状态。

代码:

#pragma GCC optimize(2)
#include<cstdio>
#include<cstring>
#include<tr1/unordered_map>
using namespace std;
using namespace tr1;
const int maxn=1e2+1e2;
const int mod=20110520;

int sta[maxn],nxt[maxn];
char in[maxn][maxn]; // in == 1 means empty .
int n,m,cur,fx,fy;
unordered_map<int,int> f[2];

inline void unzip(int* sta,int ss) {
    for(int i=m+1;i;i--) sta[i] = ss % 3 , ss /= 3;
}
inline int zip(int* sta) {
    int ret = 0;
    for(int i=1;i<=m+1;i++) ret = ret * 3 + sta[i];
    return ret;
}

inline void core_trans(unordered_map<int,int> &dst,int x,int y,int add) {
    memcpy(nxt,sta,sizeof(int)*(m+2));
    if( !in[x][y] ) { // not empty .
        if( sta[y] == 0 && sta[y+1] == 0 ) ( dst[zip(nxt)] += add ) %= mod;
        return;
    }
    if( sta[y] == 0 ) {
        if( sta[y+1] == 0 ) {
            nxt[y] = 2 , nxt[y+1] = 2 , ( dst[zip(nxt)] += add ) %= mod;
            nxt[y] = 1 , nxt[y+1] = 0 , ( dst[zip(nxt)] += add ) %= mod;
            nxt[y] = 0 , nxt[y+1] = 1 , ( dst[zip(nxt)] += add ) %= mod;
        } else if( sta[y+1] == 1 ) {
            nxt[y] = 1 , nxt[y+1] = 0 , ( dst[zip(nxt)] += add ) %= mod;
            nxt[y] = 0 , nxt[y+1] = 2 , ( dst[zip(nxt)] += add ) %= mod;
        } else if( sta[y+1] == 2 ) {
            nxt[y] = 2 , nxt[y+1] = 0 , ( dst[zip(nxt)] += add ) %= mod;
            nxt[y] = 0 , nxt[y+1] = 0 , ( dst[zip(nxt)] += add ) %= mod;
        }
    } else if( sta[y] == 1 ) {
        if( sta[y+1] == 0 ) {
            nxt[y] = 0 , nxt[y+1] = 1 , ( dst[zip(nxt)] += add ) %= mod;
            nxt[y] = 2 , nxt[y+1] = 0 , ( dst[zip(nxt)] += add ) %= mod;
        } else if( sta[y+1] == 1 ) nxt[y] = 0 , nxt[y+1] = 0 , ( dst[zip(nxt)] += add ) %= mod;
    } else if( sta[y] == 2 ) {
        if( sta[y+1] == 0 ) {
            nxt[y] = 0 , nxt[y+1] = 0 , ( dst[zip(nxt)] += add ) %= mod;
            nxt[y] = 0 , nxt[y+1] = 2 , ( dst[zip(nxt)] += add ) %= mod;
        }
    }
}
inline void trans(const unordered_map<int,int> &sou,unordered_map<int,int> &dst,int x,int y) {
    dst.clear();
    for(unordered_map<int,int>::const_iterator it=sou.begin();it!=sou.end();it++) if( it->second ) {
        unzip(sta,it->first) , core_trans(dst,x,y,it->second);
    }
}
inline void transline(const unordered_map<int,int> &sou,unordered_map<int,int> &dst) {
    dst.clear();
    for(unordered_map<int,int>::const_iterator it=sou.begin();it!=sou.end();it++) if( it->second && ! ( it->first % 3 ) ) {
        dst[it->first/3] = it->second;
    }
}

inline void revert() { // make m <= n .
    static char tp[maxn][maxn];
    memcpy(tp,in,sizeof(in)) , memset(in,0,sizeof(in));
    for(int i=1;i<=n;i++) for(int j=1;j<=m;j++) in[j][i] = tp[i][j];
    swap(n,m);
}

int main() {
    scanf("%d%d",&n,&m) , fx = -1 , fy = -1;
    for(int i=1;i<=n;i++) {
        scanf("%s",in[i]+1);
        for(int j=1;j<=m;j++) in[i][j] = in[i][j] == '_';
    }
    
    if( n < m ) revert();
    for(int i=1;i<=n&&!~fx;i++) for(int j=1;j<=m&&!~fx;j++) if(in[i][j]) fx = i , fy = j;
    if( !~fx ) return puts("1") , 0; // nothing to do .
    sta[fy] = 0 , sta[fy+1] = 1 , f[cur][zip(sta)] = 1;
    sta[fy] = 1 , sta[fy+1] = 0 , f[cur][zip(sta)] = 1;
    sta[fy] = sta[fy+1] = 2 , f[cur][zip(sta)] = 1;
    for(int j=fy+1;j<=m;j++) trans(f[cur],f[cur^1],fx,j) , cur ^= 1;
    transline(f[cur],f[cur^1]) , cur ^= 1;
    
    for(int i=fx+1;i<=n;i++) {
        for(int j=1;j<=m;j++)
            trans(f[cur],f[cur^1],i,j) , cur ^= 1;
        transline(f[cur],f[cur^1]) , cur ^= 1;
    }
    
    printf("%d
",f[cur][0]);
    
    return 0;
}

たいせつなきみのために ぼくにできるいちばんのことは
为了最重要的你 我所能做的最好的事
約束を忘れること君への想い消し去ること
就是忘却与你的约定抹去对你的思念
沈む夕日暮れてく空 夜の帳舞い降りる頃
渐渐归隐大地的夕阳 夜幕降临整个天空 夜的气息轻盈飘落之时
僕は目を閉じて それは闇に溶けるように 滲んで消えた
我闭目去感受 一切就像溶入暗影一样 渗透进去消散无痕了

未来なんていらないよ
未来（明日）什么的已经不需要了吧
君が側にいる過去のままで
因为有你一直陪伴我的往昔（昨日）