首先我们知道这棵树的形态,一眼DP。
考虑蓝线的性质,显然蓝线在树上是连接连续三个节点的。
这样就有三种情况:连接 一个节点 的 某个孩子->本身->父亲 或者 一个孩子->本身->另一个孩子。
然后胡乱写一个DP,发现并不能过大样例。
因为这种想法定义是有反例的!
考虑下面的这棵树的连边方式,怎样生成连边方式是这样的一棵树?
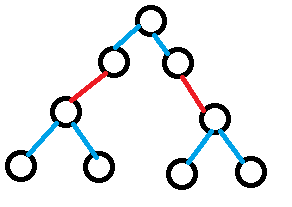
显然是不可能做到的,因为下面的两个叶子中需要有两个根才行,然而我们只能有一个根。
也就是说,确定了根以后,我们的连边方式就只剩下了 一个节点 的 某个孩子->本身->父亲 这一种。
(显然只有使用且仅使用这一种方式能生成可行的树)。
我们令f[i][0/1]表示考虑节点i及节点i的子树,i是否为蓝边的中点,能获得的最大价值。
显然我们有:
f[i][0] = sigma( j : son[i] ) max( f[j][0] , f[j][1] + edge[i->j] ) ,
f[i][1] = sigma( j : son[i] ) max( f[i][0] - max( f[j][0] , f[j][1] + edge[i->j] ) + f[j][0] + edge[i->j] )。
这样我们就能枚举根然后O(n^2)暴力DP了。
仔细观察这个转移方程,显然我们可以换根。
我们设g[i][j][0/1]表示节点i不考虑孩子j的f[i][0/1]。
我们有:
g[i][j][0] = sigma( t : son[i] && t != j ) max( f[t][0] , f[t][1] + edge[i->t] ) ,
g[i][j][1] = sigma( t : son[i] && t != j ) max( g[i][j][0] - max( f[t][0] , f[t][1] + edge[i->t] ) + f[t][0] + edge[i->t] )。
显然有:
g[i][j][0] = f[i][0] - max( f[j][0] , f[j][1] + edge[i->j] )。
对于g[i][j][1],我们可以把后面的那一堆东西提出来,那是一个仅与变量t相关的表达式。我们维护这个表达式的前缀max和后缀max就好了。
换根的话,我们就把某个节点的父亲的g[i][j][0/1]当做j的一个孩子去处理就行了。
代码:

1 #include<cstdio> 2 #include<algorithm> 3 #include<vector> 4 using namespace std; 5 const int maxn=2e5+1e2; 6 const int inf=0x3f3f3f3f; 7 8 int s[maxn],t[maxn<<1],nxt[maxn<<1],l[maxn<<1]; 9 vector<int> son[maxn],pef[maxn],suf[maxn],len[maxn]; 10 int f[maxn][2],ans; 11 12 inline void addedge(int from,int to,int len) { 13 static int cnt = 0; 14 t[++cnt] = to , l[cnt] = len , 15 nxt[cnt] = s[from] , s[from] = cnt; 16 } 17 inline void dfs1(int pos,int fa) { 18 f[pos][0] = 0 , f[pos][1] = -inf; 19 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa ) son[pos].push_back(t[at]) , len[pos].push_back(l[at]); 20 for(unsigned i=0;i<son[pos].size();i++) { 21 dfs1(son[pos][i],pos) , f[pos][0] += max( f[son[pos][i]][0] , f[son[pos][i]][1] + len[pos][i] ); 22 pef[pos].push_back(f[son[pos][i]][0]-max(f[son[pos][i]][0],f[son[pos][i]][1]+len[pos][i])+len[pos][i]) , 23 suf[pos].push_back(f[son[pos][i]][0]-max(f[son[pos][i]][0],f[son[pos][i]][1]+len[pos][i])+len[pos][i]) ; 24 } 25 for(unsigned i=0;i<son[pos].size();i++) f[pos][1] = max( f[pos][1] , f[pos][0] + pef[pos][i] ); 26 for(unsigned i=1;i<son[pos].size();i++) pef[pos][i] = max( pef[pos][i] , pef[pos][i-1] ); 27 for(int i=(signed)son[pos].size()-2;i>=0;i--) suf[pos][i] = max( suf[pos][i] , suf[pos][i+1] ); 28 } 29 inline void dfs2(int pos,int ffa0,int ffa1,int lfa) { 30 f[pos][1] += max( ffa0 , ffa1 + lfa ) , f[pos][0] += max( ffa0 , ffa1 + lfa ) , f[pos][1] = max( f[pos][1] , f[pos][0] + ffa0 - max( ffa0 , ffa1 + lfa ) + lfa ); 31 ans = max( ans , f[pos][0] ); 32 for(unsigned i=0;i<son[pos].size();i++) { 33 int fnow0 = f[pos][0] - max( f[son[pos][i]][0] , f[son[pos][i]][1] + len[pos][i] ); 34 int delta = ffa0 - max( ffa0 , ffa1 + lfa ) + lfa; 35 if( i != 0 ) delta = max( delta , pef[pos][i-1] ); 36 if( i != son[pos].size() - 1 ) delta = max( delta , suf[pos][i+1] ); 37 dfs2(son[pos][i],fnow0,fnow0+delta,len[pos][i]); 38 } 39 } 40 41 int main() { 42 static int n; 43 scanf("%d",&n); 44 for(int i=1,a,b,l;i<n;i++) scanf("%d%d%d",&a,&b,&l) , addedge(a,b,l) , addedge(b,a,l); 45 dfs1(1,-1) , dfs2(1,0,-inf,-inf) , printf("%d ",ans); 46 return 0; 47 }
(换回了U2417H的我压行更加肆无忌惮了)
