国际惯例的题面:

这题让我爆肝啦......
这种计数显然容斥,正好不含任何坏点的我们不会算,但是我们能算至少含零个坏点的,至少含一个坏点的,至少含两个坏点的......
所以最终的答案就是(至少含零个坏点的-至少含一个坏点的+至少含两个坏点的-至少含三个坏点的+至少含四个坏点的)。
然后就是怎么计算的问题。
对于至少含零个坏点的,我们不妨设定所有点都是好点。
对于非正放的正方形,我们能找到一个正好包含它的最小的正放的正方形,显然这样的正方形是唯一的。
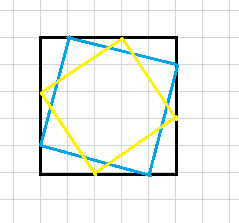
然后我们让四个点在这个正方形的边上滑动,显然这四个点的每一组位置对应一个非正放的正方形(虽然正好在四个角上的是正放的)。
于是我们可以得出总方案数为sigma( i from 1 to min(n,m) ) i * ( n - i + 1 ) * ( m - i + 1 ) 。
这个东西可以O(n)计算。
对于正好有一个坏点的,我们考虑某个以某个个点P为角的正方形A,点P一定包含这个正方形A的最小正放正方形的角上或边上。
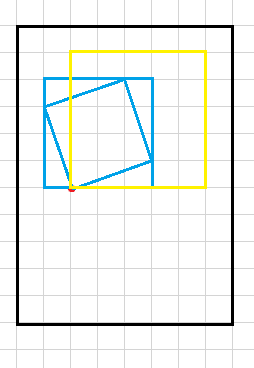
于是我们枚举这样的正方形和点P能在的位置数量就好了。
对于点P的状态,我们计算出它距离左边界的距离l,右边界距离r,上边界距离h。
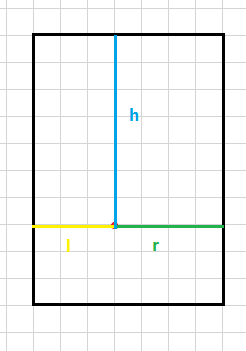
然后我们令t=min(l+r,h)。
如果我们不考虑有一些位置不能取到的话,答案应该为t*(t+3)/2。
然而这样计算了一些不能取到的位置。当t>l时,我们多计算的位置数量为(t-l)*(t-l+1)/2。(手玩一下就明白了)
t>r时同理。这样我们就能O(k)计算出至少含一个坏点的方案数。
对于正好含两及以上个坏点的,我们枚举两个坏点,显然一个正方形给你两个点,他的位置就基本确定了。
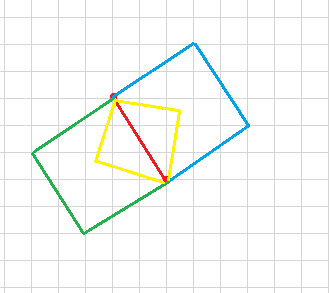
我们可以分类讨论三种情况,用向量计算出另外两个点应该在的位置。注意某些情况下以这两个点为对角线的正方形可能不在格点上。
然后对于含两个的,我们直接计算可行的正方形数;对于含三个的,我们当另外两个点有一个为坏点时计算;含四个的,我们当另外两个点均为坏点时计算。
显然含三个和含四个的我们算重了。所以应该分别除以C(3,2)和C(4,2)。
然后累加一下答案就好。
(然而计算垂直向量时没有加负号让我调了半天,老年选手身败名裂)
代码:

1 #include<cstdio> 2 #include<algorithm> 3 #include<tr1/unordered_set> 4 using namespace std; 5 using namespace tr1; 6 typedef long long int lli; 7 using namespace std; 8 using namespace tr1; 9 const int maxp=2e3+1e2; 10 const int mod=1e8+7; 11 12 struct Point { 13 int x,y; 14 friend bool operator < (const Point &a,const Point &b) { 15 return a.x != b.x ? a.x < b.x : a.y < b.y; 16 } 17 friend Point operator - (const Point &a,const Point &b) { 18 return (Point){a.x-b.x,a.y-b.y}; 19 } 20 friend Point operator + (const Point &a,const Point &b) { 21 return (Point){a.x+b.x,a.y+b.y}; 22 } 23 friend Point operator * (const Point &a,const int &b) { 24 return (Point){a.x*b,a.y*b}; 25 } 26 friend Point operator / (const Point &a,const int &b) { 27 return (Point){a.x/b,a.y/b}; 28 } 29 inline Point swp() const { 30 return (Point){y,-x}; 31 } 32 inline bool candiv() const { 33 return ( ! ( x & 1 ) ) && ( ! ( y & 1 ) ); 34 } 35 }pt[maxp]; 36 unordered_set<lli> st; 37 int n,m,t; 38 lli ans,ini,sig,dou,tri,qua; 39 40 inline void insert(const Point &p) { 41 lli h = (lli) p.x * ( m + 1 ) + p.y; 42 st.insert(h); 43 } 44 inline bool inside(const Point &p) { 45 return 0 <= p.x && p.x <= n && 0 <= p.y && p.y <= m; 46 } 47 inline bool legal(const Point &pa,const Point &pb) { 48 return inside(pa) && inside(pb); 49 } 50 inline bool have(const Point &p) { 51 lli h = (lli) p.x * ( m + 1 ) + p.y; 52 return st.find(h) != st.end(); 53 } 54 inline lli calcini(lli n,lli m) { 55 lli ret = 0 , lim = min( n , m ); 56 for(lli i=1;i<=lim;i++) ret = ( ret + ( n - i + 1 ) % mod * ( m - i + 1 ) % mod * i % mod ) % mod; 57 return ret; 58 } 59 inline lli calcedge(const lli &l,const lli &r,const lli &h) { 60 lli t = min( l + r , h ); 61 if( !t ) return 0; 62 lli ret = ( t * ( t + 3 ) >> 1 ) % mod; 63 if( t > l ) ret -= ( ( t - l ) * ( t - l + 1 ) >> 1 ) % mod; 64 if( t > r ) ret -= ( ( t - r ) * ( t - r + 1 ) >> 1 ) % mod; 65 return ( ret % mod + mod ) % mod; 66 } 67 inline lli calcsingle(lli x,lli y) { 68 const lli a = n - x , b = m - y , c = x , d = y; 69 lli ret = ( calcedge(d,b,a) + calcedge(d,b,c) + calcedge(a,c,b) + calcedge(a,c,d) ) % mod; 70 ret -= ( min(a,b) + min(b,c) + min(c,d) + min(d,a) ) % mod; 71 return ( ret % mod + mod ) % mod; 72 } 73 inline lli calcdouble(const Point &a,const Point &b) { 74 const Point delta = (a-b).swp(); 75 int ret = legal(a+delta,b+delta) + legal(a-delta,b-delta); 76 const Point mid = a + b , pa = mid + delta , pb = mid - delta; 77 if( pa.candiv() && pb.candiv() && legal(pa/2,pb/2) ) ++ret; 78 return ret; 79 } 80 inline lli calctriple(const Point &a,const Point &b) { 81 const Point delta = (a-b).swp(); 82 int ret = 0; 83 if( legal(a+delta,b+delta) ) ret += have(a+delta) + have(b+delta); 84 if( legal(a-delta,b-delta) ) ret += have(a-delta) + have(b-delta); 85 const Point mid = a + b , pa = mid + delta , pb = mid - delta; 86 if( pa.candiv() && pb.candiv() && legal(pa/2,pb/2) ) ret += have(pa/2) + have(pb/2); 87 return ret; 88 } 89 inline lli calcquad(const Point &a,const Point &b) { 90 const Point delta = (a-b).swp(); 91 int ret = 0; 92 if( legal(a+delta,b+delta) ) ret += ( have(a+delta) && have(b+delta) ); 93 if( legal(a-delta,b-delta) ) ret += ( have(a-delta) && have(b-delta) ); 94 const Point mid = a + b , pa = mid + delta , pb = mid - delta; 95 if( pa.candiv() && pb.candiv() && legal(pa/2,pb/2) ) ret += ( have(pa/2) && have(pb/2) ); 96 return ret; 97 } 98 99 int main() { 100 scanf("%d%d%d",&n,&m,&t); 101 for(int i=1;i<=t;i++) scanf("%d%d",&pt[i].x,&pt[i].y) , insert(pt[i]); 102 ini = calcini(n,m); 103 for(int i=1;i<=t;i++) sig += calcsingle(pt[i].x,pt[i].y); 104 for(int i=1;i<=t;i++) for(int j=i+1;j<=t;j++) { 105 dou += calcdouble(pt[i],pt[j]) , tri += calctriple(pt[i],pt[j]) , qua += calcquad(pt[i],pt[j]); 106 } 107 tri /= 3 , qua /= 6; 108 ans = ( ( ini - sig + dou - tri + qua ) % mod + mod ) % mod; 109 printf("%lld ",ans); 110 return 0; 111 }
