Bzoj5251 线段树+贪心
记录本蒟蒻省选后的第一篇题解!
国际惯例的题面: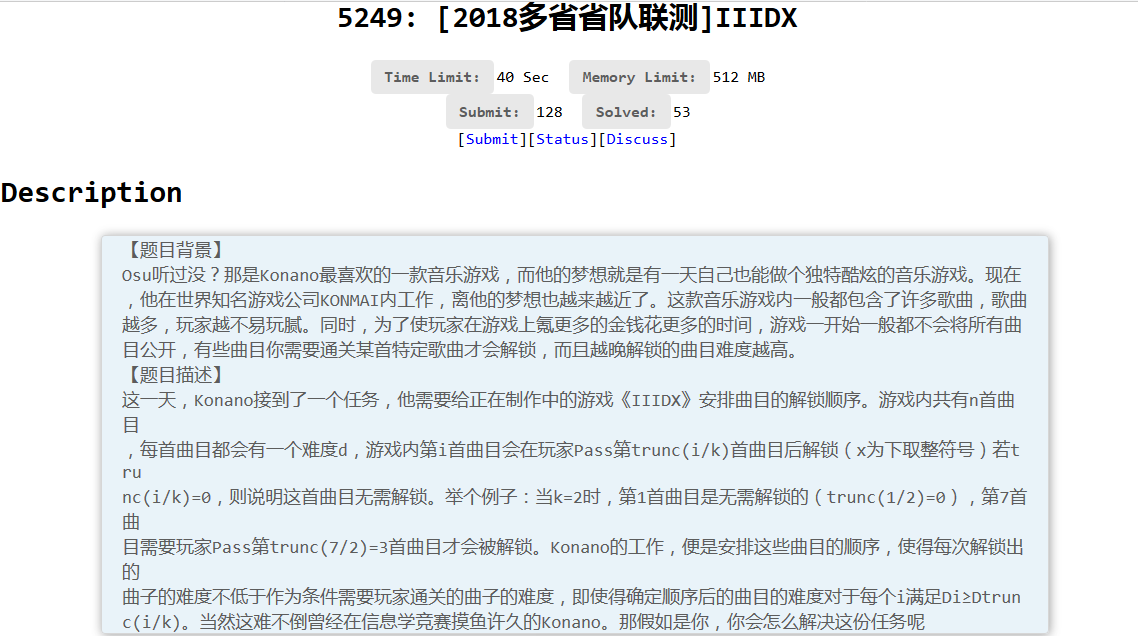
首先这个东西显然是一棵树。
如果我们把数值排序,并建立这棵树的dfs序,显然dfs序上的一个区间对应数值的一个区间,且根为数值区间左端点。
如果你这样想,恭喜你能获得50分,如果记得加了eps会获得55~60分。
因为当数值可以相同的时候,这个贪心是存在反例的。
考虑10个点的二叉堆,9个1一个2,显然2应该在位置6,而这样跑出来2会在位置10!
因为可能一个子树的数值是不连续的,我们可以在把根节点的位置减小为相同数值的左一个的时候,把这个区间的一个值分给别的子树。
考虑修正贪心。
我们离散化序列,记录每个值出现次数。
然后我们令f[i]表示>=i的数的个数。
先统计出子树size,考虑bfs遍历整个子树。
这样我们子树的根节点x要选择的就是满足f[1,i]均>=siz[x]的最大的i,我们令ans[x]=i。
之后我们需要让f[1,i]减去siz[x],为了给这个子树预留位置。
当然,在遍历到一个节点的时候需要把为他的父亲预留的size加回去,也就是说,让f[1,ans[fa[x]]]加上siz[fa[x]]-1。
这个线段树二分怎么实现?由于这个序列不单调,我们维护区间min,如果左区间的min>=siz[x]的话就去右区间查询。
最后特判当前的点能否选择即可。
(考试的时候想到了线段树,但是非得用dfs序列遍历,怎么也弄不对......)
注意这题BZOJ卡eps!!!!!
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define debug cout 6 using namespace std; 7 const int maxn=5e5+1e2; 8 const double eps=1e-8; 9 10 int in[maxn],srt[maxn],siz[maxn],len; 11 int ans[maxn],fa[maxn],ts[maxn],vis[maxn]; 12 int n; 13 14 struct SegmentTree { 15 int l[maxn<<3],r[maxn<<3],lson[maxn<<3],rson[maxn<<3],lazy[maxn<<3],mi[maxn<<3],cnt; 16 inline void build(int pos,int ll,int rr) { 17 l[pos] = ll , r[pos] = rr; 18 if( ll == rr ) return; 19 const int mid = ( ll + rr ) >> 1; 20 build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr); 21 } 22 inline void apply(int pos,int delta) { 23 mi[pos] += delta , lazy[pos] += delta; 24 } 25 inline void push(int pos) { 26 if( !lazy[pos] || l[pos] == r[pos] ) return; 27 apply(lson[pos],lazy[pos]) , apply(rson[pos],lazy[pos]) , lazy[pos] = 0; 28 } 29 inline void maintain(int pos) { 30 if( l[pos] == r[pos] ) return; 31 mi[pos] = min( mi[lson[pos]] , mi[rson[pos]] ); 32 } 33 inline void update(int pos,int ll,int rr,int delta) { 34 if( r[pos] < ll || rr < l[pos] ) return; 35 if( ll <= l[pos] && r[pos] <= rr ) return apply(pos,delta); 36 push(pos); 37 update(lson[pos],ll,rr,delta) , update(rson[pos],ll,rr,delta); 38 maintain(pos); 39 } 40 inline int query(int pos,int lim) { 41 if( l[pos] == r[pos] ) return mi[pos] >= lim ? l[pos] : l[pos] - 1; 42 push(pos); 43 if( mi[lson[pos]] >= lim ) return query(rson[pos],lim); 44 else return query(lson[pos],lim); 45 } 46 }segt; 47 48 inline void getseq() { 49 sort(in+1,in+1+n); 50 srt[len=1] = in[1] , siz[1] = 1; 51 for(int i=2;i<=n;i++) { 52 if( in[i] != in[i-1] ) srt[++len] = in[i]; 53 ++siz[len]; 54 } 55 segt.build(segt.cnt=1,1,len); 56 for(int i=1;i<=len;i++) segt.update(1,1,i,siz[i]); 57 } 58 59 inline void calcpoint(int x) { 60 if( fa[x] && !vis[fa[x]] ) segt.update(1,1,ans[fa[x]],ts[fa[x]]-1) , vis[fa[x]] = 1; 61 int fd = segt.query(1,ts[x]); ans[x] = fd; 62 segt.update(1,1,fd,-ts[x]); 63 } 64 65 int main() { 66 static double k; 67 scanf("%d%lf",&n,&k); 68 for(int i=1;i<=n;i++) scanf("%d",in+i) , fa[i] = (int) ( (double) i / k + eps ) , ts[i] = 1; 69 getseq(); 70 for(int i=n;i;i--) if( fa[i] ) ts[fa[i]] += ts[i]; 71 for(int i=1;i<=n;i++) calcpoint(i); 72 for(int i=1;i<=n;i++) printf("%d%c",srt[ans[i]],i!=n?' ':' '); 73 return 0; 74 }
