北京集训:20180325

你说我怎么这么菜呢?

T1:

考场上没看到下取整，同时把那个sigma看成了次数，以为要在mod phi(p)下算，这玩意能做？
然后果断爆零......
其实puts(2的逆元)+puts("1")有25分......
正解看官方题解吧。

那个鬼畜的容斥大概就是在n+1个断点中钦定k个断点，数字相对于剩下的m+1-k个集合的位置无关，所以对于这m+1-k个集合可以随意放置。
代码:

#include<cstdio>
#include<algorithm>
typedef long long int lli;
const int maxn=1e5+1e2,maxl=262145;
const int mod=998244353,g=3;

lli fac[maxn],inv[maxn];
lli lft[maxl],rit[maxl],tar[maxl];
lli ans;
int n,m;

inline lli fastpow(lli base,int tim) {
    lli ret = 1;
    while( tim ) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}
inline void NTT(lli* dst,int n,int ope=1) {
    for(int i=0,j=0;i<n;i++) {
        if( i < j ) std::swap(dst[i],dst[j]);
        for(int t=n>>1;(j^=t)<t;t>>=1);
    }
    for(int len=2;len<=n;len<<=1) {
        const int h = len >> 1;
        lli per = fastpow(g,mod/len);
        if( !~ope ) per = fastpow(per,mod-2);
        for(int st=0;st<n;st+=len) {
            lli w = 1;
            for(int pos=0;pos<h;pos++) {
                const lli u = dst[st+pos] , v = dst[st+pos+h] * w % mod;
                dst[st+pos] = ( u + v ) % mod ,
                dst[st+pos+h] = ( u - v + mod ) % mod ,
                w = w * per % mod;
            }
        }
    }
    if( !~ope ) {
        const lli inv = fastpow(n,mod-2);
        for(int i=0;i<n;i++) dst[i] = dst[i] * inv % mod;
    }
}

inline lli c(int n,int m) {
    return fac[n] * inv[m] % mod * inv[n-m] % mod;
}
inline void init() {
    for(int i=0;i<=n+1;i++) {
        lft[i] = ( i & 1 ) ? mod - c(n+1,i) : c(n+1,i);
        rit[i] = fastpow(i,n);
    }
}
inline void getans() {
    init(); int len = 1;
    while( len <= ( n << 1 ) + 1 ) len <<= 1;
    NTT(lft,len) , NTT(rit,len);
    for(int i=0;i<len;i++) tar[i] = lft[i] * rit[i] % mod;
    NTT(tar,len,-1);
    for(int i=0;i<=n;i++) ans = ( ans + tar[i+1] * fastpow(i,m) % mod ) % mod;
    ans = ans * inv[n] % mod;
}
inline void pre() {
    int lim = n + 1;
    *fac = 1;
    for(int i=1;i<=lim;i++) fac[i] = fac[i-1] * i % mod;
    inv[lim] = fastpow(fac[lim],mod-2);
    for(int i=lim;i;i--) inv[i-1] = inv[i] * i % mod;
}

int main() {
    scanf("%d%d",&n,&m);
    pre() , getans();
    printf("%lld
",ans);
    return 0;
}

T2:

n方暴力很好写吧......
考虑二维平面，一条路径相当于让两边花式取min，然后不会写了。
写了一个大力random_shuffle也没有骗到subtask2的分......
正解是分治，考虑我们把这个东西划分成多个三角形，然后枚举中间的一条边，分别计算经过这条边两个点的询问的代价并递归计算两边询问的代价。
因为显然两个点分别在这条边两边的询问的最有路径至少过这条边两个端点中的一个......
然而这种分治可能把一个求解区间变成上下两个不连通的联通快......所以在更新时需要特判一下-1，在递归边界也要特判......
话说第一次写这个我还写傻了，写了8kb代码死活调不出来......后来重构了才成功AC。
25分暴力代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#define debug cout
using namespace std;
const int maxn=1e5+1e2;

struct Node {
    int y,id;
};
struct QNode {
    int siz,id;
    friend bool operator < (const QNode &a,const QNode &b) {
        return a.siz < b.siz;
    }
};
vector<Node> qs[maxn];
priority_queue<QNode> pq;
queue<int> q;
vector<int> vec[maxn];
int siz[maxn],dis[maxn],ans[maxn];
int n,m;

inline void bfs(int st) {
    memset(dis,-1,sizeof(int)*n) , dis[st] = 0;
    q.push(st);
    while( q.size() ) {
        const int pos = q.front(); q.pop();
        for(unsigned j=0;j<vec[pos].size();j++)
            if( !~dis[vec[pos][j]] )
                dis[vec[pos][j]] = dis[pos] + 1 ,
                q.push(vec[pos][j]);
    }
}
inline void getans(const QNode &d) {
    if( siz[d.id] != d.siz ) return;
    const int id = d.id; bfs(id);
    for(unsigned i=0;i<qs[id].size();i++)
        if( !ans[qs[id][i].id] ) {
            ans[qs[id][i].id] = dis[qs[id][i].y] ,
            pq.push((QNode){--siz[qs[id][i].y],qs[id][i].y});
        }
}
inline void getans() {
    while( pq.size() ) {
        getans(pq.top()) , pq.pop();
    }
}
inline void shufall() {
    srand(19260817);
    for(int i=0;i<n;i++) random_shuffle(vec[i].begin(),vec[i].end());
}

int main() {
    scanf("%d",&n);
    for(int i=0;i<n;i++) {
        vec[i].push_back(i!=n-1?i+1:0) ,
        vec[i].push_back(i?i-1:n-1);
    }
    for(int i=1,a,b;i<=n-3;i++) {
        scanf("%d%d",&a,&b) ,
        vec[a].push_back(b) ,
        vec[b].push_back(a) ;
    }
    shufall() , scanf("%d",&m);
    for(int i=1,a,b;i<=m;i++) {
        scanf("%d%d",&a,&b);
        qs[a].push_back((Node){b,i}) ,
        qs[b].push_back((Node){a,i}) ;
    }
    for(int i=0;i<n;i++) pq.push((QNode){siz[i]=qs[i].size(),i});
    getans();
    for(int i=1;i<=m;i++) printf("%d
",ans[i]);
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<vector>
#include<queue>
#include<cstdlib>
#define debug cout
using namespace std;
const int maxn=1e5+1e2;
const int inf=0x3f3f3f3f;

struct Query {
    int a,b,id;
};
int s[maxn],t[maxn<<2],nxt[maxn<<2];
int disx[maxn],disy[maxn],id[maxn],pt[maxn],iid,cnt;
vector<Query> qs;
vector<int> ps;
int ans[maxn];

inline void addedge(int from,int to) {
    static int cnt = 0;
    t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
    swap(from,to);
    t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
}

inline void bfs(int st,int* dis) {
    queue<int> q; dis[st] = 0 , q.push(st);
    while( q.size() ) {
        const int pos = q.front(); q.pop();
        for(int at=s[pos];at;at=nxt[at])
            if( !~dis[t[at]] && id[t[at]] == id[pos] )
                dis[t[at]] = dis[pos] + 1 , q.push(t[at]);
    }
}

inline void solve(const vector<int> &ps,const vector<Query> &qs) {
    if( !qs.size() ) return;
    if( ps.size() <= 3 ) {
        ++iid;
        for(unsigned i=0;i<ps.size();i++) disx[ps[i]] = disy[ps[i]] = -1 , id[ps[i]] = iid;
        int x = ps[0] , y = ps[1];
        bfs(x,disx) , bfs(y,disy);
        for(unsigned i=0;i<qs.size();i++) {
            if( ~disx[qs[i].a] && ~disx[qs[i].b] ) ans[qs[i].id] = min( ans[qs[i].id] , disx[qs[i].a] + disx[qs[i].b] );
            if( ~disy[qs[i].a] && ~disy[qs[i].b] ) ans[qs[i].id] = min( ans[qs[i].id] , disy[qs[i].a] + disy[qs[i].b] );
        }
        return;
    }
    ++iid , cnt = 0;
    for(unsigned i=0;i<ps.size();i++) {
        disx[ps[i]] = disy[ps[i]] = -1 ,
        id[ps[i]] = iid , pt[ps[i]] = ++cnt;
    }
    int miv = inf , x = 0 , y = 0;
    for(unsigned i=0;i<ps.size();i++) {
        const int pos = ps[i];
        for(int at=s[pos];at;at=nxt[at])
            if( id[t[at]] == iid ) {
                const int lam = max( abs(pt[t[at]]-pt[pos]) , (signed) ps.size() - abs(pt[t[at]]-pt[pos]) );
                if( lam < miv ) miv = lam , x = pos , y = t[at];
            }
    }
    if( pt[x] > pt[y] ) swap(x,y);
    bfs(x,disx) , bfs(y,disy);
    vector<int> pl,pr;
    vector<Query> ql,qr;
    for(unsigned i=0;i<qs.size();i++) {
        if( ~disx[qs[i].a] && ~disx[qs[i].b] ) ans[qs[i].id] = min( ans[qs[i].id] , disx[qs[i].a] + disx[qs[i].b] );
        if( ~disy[qs[i].a] && ~disy[qs[i].b] ) ans[qs[i].id] = min( ans[qs[i].id] , disy[qs[i].a] + disy[qs[i].b] );
        if( qs[i].a == x || qs[i].b == x || qs[i].a == y || qs[i].b == y ) continue;
        if( pt[x] < pt[qs[i].a] && pt[qs[i].a] < pt[y] && pt[x] < pt[qs[i].b] && pt[qs[i].b] < pt[y] ) ql.push_back(qs[i]);
        if( ! ( pt[x] <= pt[qs[i].a] && pt[qs[i].a] <= pt[y] ) && ! ( pt[x] <= pt[qs[i].b] && pt[qs[i].b] <= pt[y] ) ) qr.push_back(qs[i]);
    }
    for(unsigned i=0;i<ps.size();i++) {
        if( ps[i] == x || ps[i] == y ) continue;
        if( pt[x] < pt[ps[i]] && pt[ps[i]] < pt[y] ) pl.push_back(ps[i]);
        if( ! ( pt[x] <= pt[ps[i]] && pt[ps[i]] <= pt[y] ) ) pr.push_back(ps[i]);
    }
    solve(pl,ql) , solve(pr,qr);
}

int main() {
    static int n,m;
    scanf("%d",&n);
    for(int i=0;i<n;i++) {
        addedge(i,(i+1)%n) ,
        ps.push_back(i);
    }
    for(int i=1,a,b;i<=n-3;i++)
        scanf("%d%d",&a,&b) , addedge(a,b);
    scanf("%d",&m) , memset(ans,0x3f,sizeof(ans));
    for(int i=1,a,b;i<=m;i++) {
        scanf("%d%d",&a,&b) , qs.push_back((Query){a,b,i});
    }
    solve(ps,qs);
    for(int i=1;i<=m;i++) printf("%d
",ans[i]);
    return 0;
}

写傻了的代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<set>
#include<map>
#include<queue>
#include<vector>
#include<cassert>
#define debug cout
using namespace std;
const int maxn=1e5+1e2;
const int inf=0x3f3f3f3f;

struct Query {
    int a,b,id;
};
vector<pair<int,int> > es;
vector<Query> qs;
vector<int> tp,ps;
int ans[maxn],n,m;

namespace Graph {
    int s[maxn],t[maxn<<2],nxt[maxn<<2],disx[maxn],disy[maxn];
    queue<int> q;
    
    inline void coredge(int from,int to) {
        static int cnt = 0;
        t[++cnt] = to , nxt[cnt] = s[from] , s[from] = cnt;
    }
    inline void doubledge(int a,int b) {
        coredge(a,b) , coredge(b,a);
    }
    inline void bfs(int st,int* dis) {
        q.push(st) , dis[st] = 0;
        while( q.size() ) {
            const int pos = q.front(); q.pop();
            for(int at=s[pos];at;at=nxt[at]) if( !~dis[t[at]] )
                dis[t[at]] = dis[pos] + 1 , q.push(t[at]);
        }
    }
    inline void solve(const vector<int> &ps,const vector<Query> &qs,int x,int y) {
        for(unsigned i=0;i<ps.size();i++) disx[ps[i]] = disy[ps[i]] = -1;
        bfs(x,disx) , bfs(y,disy);
        for(unsigned i=0;i<qs.size();i++) {
            ans[qs[i].id] = min( ans[qs[i].id] , min( disx[qs[i].a] + disy[qs[i].b] , disx[qs[i].b] + disy[qs[i].a] ) + 1 );
            ans[qs[i].id] = min( ans[qs[i].id] , min( disx[qs[i].a] + disx[qs[i].b] , disy[qs[i].b] + disy[qs[i].a] ) );
        }
    }
}

namespace TreeDivideAndConqure {
    int s[maxn],t[maxn<<1],nxt[maxn<<1],x[maxn<<1],y[maxn<<1];
    int id[maxn],siz[maxn],iid,miv,mip,mipfa;
    inline void coredge(int from,int to,int xx,int yy) {
        static int cnt = 0;
        //debug<<"from = "<<from<<"to = "<<to<<endl;
        t[++cnt] = to , x[cnt] = xx , y[cnt] = yy ,
        nxt[cnt] = s[from] , s[from] = cnt;
    }
    inline void addedge(int a,int b,int xx,int yy) {
        int x = min( x , xx ) , y = max( y , yy );
        coredge(a,b,x,y) , coredge(b,a,x,y);
    }
}

namespace GetTriangle {
    struct Triangle {
        int x,y,z;
        Triangle() { x = y = z = -1; }
        Triangle(int xx,int yy,int zz) {
            static int tp[3];
            tp[0] = xx , tp[1] = yy , tp[2] = zz;
            sort(tp,tp+3);
            //debug<<"x = "<<xx<<"y = "<<yy<<"z = "<<zz<<endl;
            x = tp[0] , y = tp[1] , z = tp[2];
        }
        friend bool operator < (const Triangle &a,const Triangle &b) {
            if( a.x != b.x ) return a.x < b.x;
            if( a.y != b.y ) return a.y < b.y;
            return a.z < b.z;
        }
    }rec[maxn];
    
    priority_queue<pair<unsigned,int> > pq;
    map<Triangle,int> mp;
    set<int> es[maxn];
    int deg[maxn],tcnt;
    
    inline void getdualpoint(const int &x,int &y,int &z) {
        y = z = -1;
        for(set<int>::iterator it=es[x].begin();it!=es[x].end();it++) {
            if( !~y ) y = *it;
            else z = *it;
        }
    }
    inline Triangle getbypoint(const int &x) {
        assert(es[x].size()==2);
        int y,z;
        getdualpoint(x,y,z);
        return Triangle(x,y,z);
    }
    inline void cutpoint(const pair<unsigned,int> &pir) {
        const int x = pir.second;
        if( -pir.first != es[x].size() ) return;
        if( es[x].size() < 2 ) return;
        //debug<<"in cutpoint x = "<<pir.second<<endl;
        int y,z;
        getdualpoint(x,y,z);
        //debug<<"y = "<<y<<"z = "<<z<<endl;
        Triangle now = Triangle(x,y,z) , nxt;
        if( mp.find(now) == mp.end() ) mp[now] = ++tcnt , rec[tcnt] = now;
        es[x].erase(y) , es[y].erase(x) ,
        es[x].erase(z) , es[z].erase(x) ;
        if( es[y].size() == 2 ) nxt = getbypoint(y);
        else if( es[z].size() == 2 ) nxt = getbypoint(z);
        if( ~nxt.x ) {
            if( mp.find(nxt) == mp.end() ) mp[nxt] = ++tcnt , rec[tcnt] = nxt;
            TreeDivideAndConqure::addedge(mp[now],mp[nxt],y,z);
        }
        pq.push(make_pair(-es[y].size(),y)) , pq.push(make_pair(-es[z].size(),z));
    }
    inline void work() {
        for(int i=0;i<n;i++) pq.push(make_pair(-es[i].size(),i));
        while( pq.size() ) cutpoint(pq.top()) , pq.pop();
    }
}

namespace TreeDivideAndConqure {
    inline void dfs(int pos,int fa,const int &fs,int &rx,int &ry) {
        //debug<<"pos = "<<pos<<endl;
        siz[pos] = 1;
        for(int at=s[pos];at;at=nxt[at])
            if( id[t[at]] == iid && t[at] != fa ) {
                dfs(t[at],pos,fs,rx,ry) , siz[pos] += siz[t[at]];
                //debug<<"max = "<<max(siz[t[at]],fs-siz[t[at]])<<endl;
                if( max(siz[t[at]],fs-siz[t[at]]) < miv ) {
                    
                    rx = x[at] , ry = y[at] ,
                    miv = max(siz[t[at]],fs-siz[t[at]]) ,
                    mip = t[at] , mipfa = pos;
                }
            }
    }
    inline void spit(int pos,int fa,vector<int> &ret) {
        ret.push_back(pos);
        for(int at=s[pos];at;at=nxt[at])
            if( id[t[at]] == iid && t[at] != fa )
                spit(t[at],pos,ret);
    }
    #define judge1(l,r,x) ( l < x && x < r )
    #define judge2(l,r,x) ( ! ( l <= x && x <= r ) )
    inline void solve(const vector<int> &tps,const vector<int> &ps,const vector<pair<int,int> > es,const vector<Query> qs) {
        if( tps.size() < 1 || ps.size() <= 1 || !es.size() || !qs.size() ) return;
        //debug<<"in solve"<<endl;
        ++iid;
        for(unsigned i=0;i<tps.size();i++) id[tps[i]] = iid;
        //debug<<"tps = "; for(unsigned i=0;i<tps.size();i++) debug<<tps[i]<<" "; debug<<endl;
        //debug<<"ps = "; for(unsigned i=0;i<ps.size();i++) debug<<ps[i]<<" "; debug<<endl;
        int x,y;
        miv = inf , dfs(tps[0],-1,tps.size(),x,y);
        //debug<<"x = "<<x<<"y = "<<y<<endl;
        Graph::solve(ps,qs,x,y);
        vector<int> tpl,tpr;
        spit(mip,mipfa,tpl) , spit(mipfa,mip,tpr);
        vector<int> pl,pr;
        vector<pair<int,int> > el,er;
        vector<Query> ql,qr;
        for(unsigned i=0;i<ps.size();i++) {
            if( judge1(x,y,ps[i]) ) pl.push_back(ps[i]);
            if( judge2(x,y,ps[i]) ) pr.push_back(ps[i]);
        }
        for(unsigned i=0;i<es.size();i++) {
            if( judge1(x,y,es[i].first) && judge1(x,y,es[i].second) ) el.push_back(es[i]);
            if( judge2(x,y,es[i].first) && judge2(x,y,es[i].second) ) er.push_back(es[i]);
        }
        for(unsigned i=0;i<qs.size();i++) {
            if( judge1(x,y,qs[i].a) && judge1(x,y,qs[i].b) ) ql.push_back(qs[i]);
            if( judge2(x,y,qs[i].a) && judge2(x,y,qs[i].b) ) qr.push_back(qs[i]);
        }
        if( tpl.size() && tpr.size() && GetTriangle::rec[tpl[0]].x > GetTriangle::rec[tpr[0]].x ) swap(tpl,tpr);
        /*debug<<"tpl = "; for(unsigned i=0;i<tpl.size();i++) debug<<tpl[i]<<" "; debug<<endl;
        debug<<"tpr = "; for(unsigned i=0;i<tpr.size();i++) debug<<tpr[i]<<" "; debug<<endl;
        debug<<"pl = "; for(unsigned i=0;i<pl.size();i++) debug<<pl[i]<<" "; debug<<endl;
        debug<<"pr = "; for(unsigned i=0;i<pr.size();i++) debug<<pr[i]<<" "; debug<<endl;*/
        solve(tpl,pl,el,ql) , solve(tpr,pr,er,qr);
    }
}

inline void addedge(int x,int y) {
    if( x > y ) swap(x,y);
    es.push_back(make_pair(x,y));
    GetTriangle::es[x].insert(y) , GetTriangle::es[y].insert(x);
    Graph::doubledge(x,y);
}
int main() {
    static int m;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
        addedge(i,(i+1)%n);
    for(int i=1,a,b;i<=n-3;i++)
        scanf("%d%d",&a,&b) , addedge(a,b);
    scanf("%d",&m);
    for(int i=1,a,b;i<=m;i++) {
        scanf("%d%d",&a,&b);
        qs.push_back((Query){a,b,i});
    }
    memset(ans,0x3f,sizeof(ans));
    GetTriangle::work();
    //for(unsigned i=1;i<=GetTriangle::tcnt;i++) debug<<GetTriangle::rec[i].x<<" "<<GetTriangle::rec[i].y<<" "<<GetTriangle::rec[i].z<<endl;
    //exit(0);
    for(int i=0;i<n;i++) ps.push_back(i);
    for(int i=1;i<=GetTriangle::tcnt;i++) tp.push_back(i);
    TreeDivideAndConqure::solve(tp,ps,es,qs);
    for(int i=1;i<=m;i++)
        printf("%d
",ans[i]);
    return 0;
}

T3:

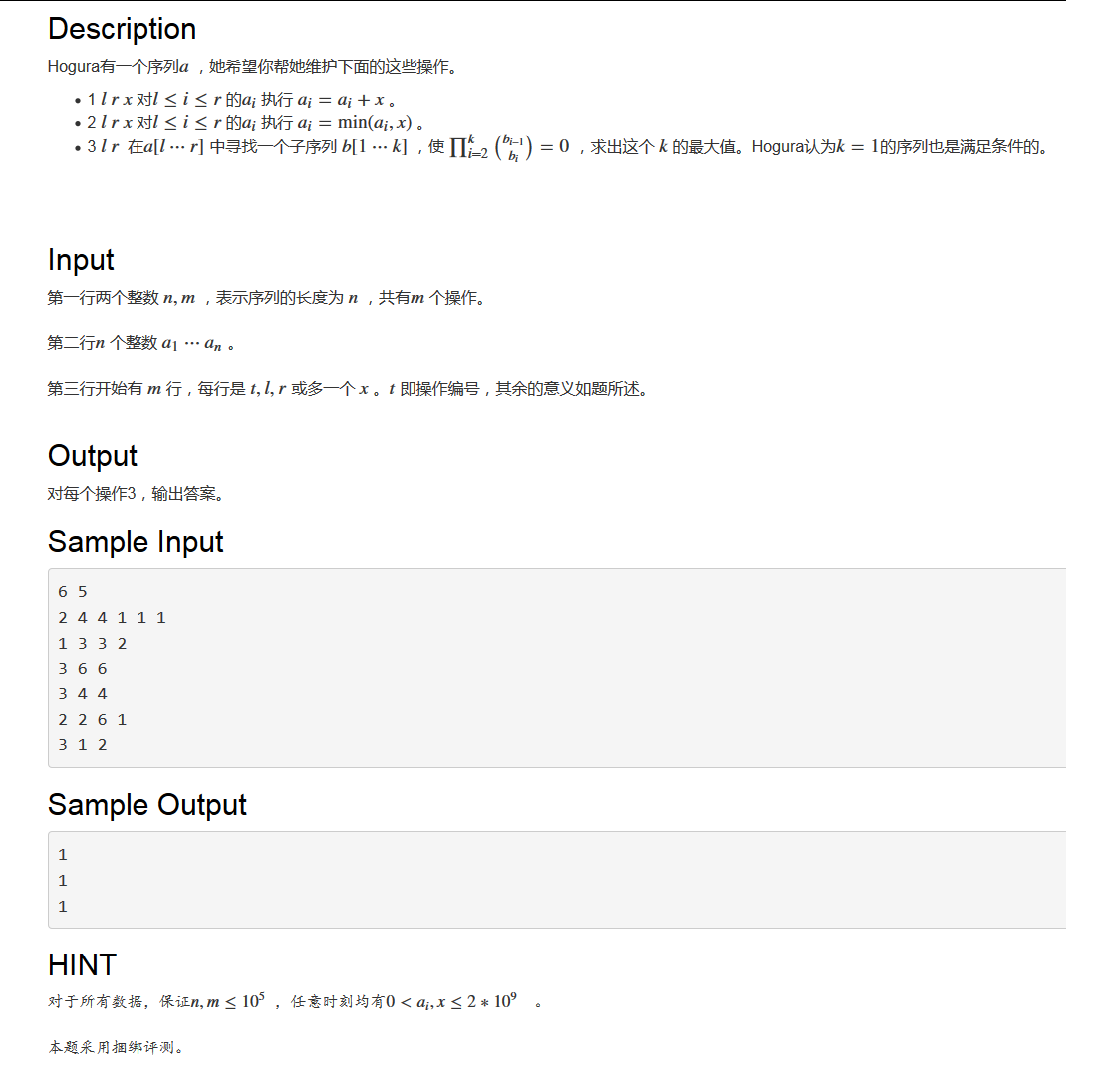
显然答案不能在区间不是单调不增的时候为len，否则为1。
n方暴力依然好写。
只有加的情况也很容易。
于是我考场上写了自调整分块trick过了40分......
但是在处理取min的时候存在问题，不能AC。
正解是线段树，然而我并不会jry线段树。
于是考虑乱搞，维护区间min，区间max，后面有一个更大的值的最小的umin，然后合并时讨论一下就好了。
两个标记的话让加法优于取min，因为我们能在min上进行加法修改。应用的时候先加法即可。
40分分块代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=1e5+1e2,maxb=319;
const lli inf=0x3f3f3f3f3f3f3f3fll;

int bel[maxn],st[maxb],ed[maxb];
lli in[maxn],lazy_add[maxb],lazy_min[maxb],mxv[maxb],miv[maxb];
bool flag[maxb];
int n;

inline void block_add(int pos,int l,int r,lli t) {
    l = max( l , st[pos] ) , r = min( r , ed[pos] ) , flag[pos] = 0;
    for(int i=l;i<=r;i++) {
        in[i] += t;
        if( i != l ) flag[pos] |= ( in[i-1] < in[i] );
    }
}
inline void block_min(int pos,int l,int r,lli t) {
    l = max( l , st[pos] ) , r = min( r , ed[pos] ) , flag[pos] = 0;
    for(int i=l;i<=r;i++) {
        in[i] = min( in[i] , t );
        if( i != l ) flag[pos] |= ( in[i-1] < in[i] );
    }
}
inline void rebuild_blk(int pos) {
    miv[pos] = inf , mxv[pos] = 0 , flag[pos] = 0;
    for(int i=st[pos];i<=ed[pos];i++) {
        miv[pos] = min( miv[pos] , in[i] ) ,
        mxv[pos] = max( mxv[pos] , in[i] ) ;
        if( i != st[pos] ) flag[pos] |= ( in[i-1] < in[i] ) ;
    }
}
inline void push_lazy(int pos) {
    int fail = 1;
    if( lazy_add[pos] ) {
        block_add(pos,st[pos],ed[pos],lazy_add[pos]);
        lazy_add[pos] = 0 , fail = 0;
    }
    if( lazy_min[pos] < inf ) {
        block_min(pos,st[pos],ed[pos],lazy_min[pos]);
        lazy_min[pos] = inf , fail = 0;
    }
    if( !fail ) rebuild_blk(pos);
}
inline void fully_add(int pos,lli x) {
    lazy_add[pos] += x , lazy_min[pos] += x ,
    miv[pos] += x , mxv[pos] += x;
}
inline void fully_min(int pos,lli x) {
    lazy_min[pos] = min( miv[pos] , x ) ,
    miv[pos] = min( miv[pos] , x ) ,
    mxv[pos] = min( mxv[pos] , x ) ;
}
inline void partly_add(int pos,int l,int r,lli x) {
    push_lazy(pos) ,
    block_add(pos,l,r,x) ,
    rebuild_blk(pos) ;
}
inline void partly_min(int pos,int l,int r,lli x) {
    push_lazy(pos) ,
    block_min(pos,l,r,x) ,
    rebuild_blk(pos) ;
}
inline void update_add(int l,int r,lli x) {
    if( bel[l] == bel[r] ) return partly_add(bel[l],l,r,x);
    for(int i=bel[l]+1;i<bel[r];i++) fully_add(i,x);
    partly_add(bel[l],l,r,x) , partly_add(bel[r],l,r,x);
}
inline void update_min(int l,int r,lli x) {
    if( bel[l] == bel[r] ) return partly_min(bel[l],l,r,x);
    for(int i=bel[l]+1;i<bel[r];i++) fully_min(i,x);
    partly_min(bel[l],l,r,x) , partly_min(bel[r],l,r,x);
}
inline bool query_part(int pos,int l,int r,lli& miv,lli& mxv) {
    push_lazy(pos);
    l = max( l , st[pos] ) , r = min( r , ed[pos] );
    miv = inf , mxv = 0;
    bool ret = 0;
    for(int i=l;i<=r;i++) {
        miv = min( miv , in[i] ) , mxv = max( mxv , in[i] ) ;
        if( i != l ) ret |= ( in[i-1] < in[i] );
    }
    return ret;
}
inline bool query(int l,int r) {
    lli smiv,tp,x;
    if( bel[l] == bel[r] ) return query_part(bel[l],l,r,smiv,tp);
    bool ret = query_part(bel[l],l,r,smiv,tp);
    for(int i=bel[l]+1;i<bel[r];i++) {
        ret |= flag[i] , ret |= ( smiv < mxv[i] ) , smiv = min( smiv , miv[i] );
        if( ret ) return ret;
    }
    ret |= query_part(bel[r],l,r,x,tp) , ret |= ( smiv < tp );
    return ret;
}

inline void build(bool flag) {
    const int blksiz = flag ? n : sqrt(n);
    int cnt = 0;
    for(int l=1,r;l<=n;l=r+1) {
        r = min( l + blksiz - 1 , n ) , ++cnt;
        st[cnt] = l , ed[cnt] = r , lazy_min[cnt] = inf;
        for(int i=l;i<=r;i++) bel[i] = cnt;
        rebuild_blk(cnt);
    }
}

int main() {
    static int m;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++) scanf("%lld",in+i);
    build(n<=1000);
    for(int i=1,t,l,r,x;i<=m;i++) {
        scanf("%d%d%d",&t,&l,&r);
        if( t == 3 ) printf("%d
",query(l,r)?r-l+1:1);
        else {
            scanf("%d",&x);
            if( t == 1 ) update_add(l,r,x);
            else if( t == 2 ) update_min(l,r,x);
        }
    }
    return 0;
}

正解代码:

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#define debug cout
typedef long long int lli;
using namespace std;
const int maxn=1e5+1e2;
const lli inf=0x3f3f3f3f3f3f3f3fll,lim=inf>>4;

struct Node {
    lli miv,mxv,umiv,umxv;
    friend Node operator + (const Node &a,const Node &b) {
         Node ret = (Node){min(a.miv,b.miv),max(a.mxv,b.mxv),inf,-inf};
         if( a.miv < b.mxv ) ret.umiv = a.miv , ret.umxv = b.mxv;
         if( a.umiv < ret.umiv ) ret.umiv = a.umiv , ret.mxv = max( a.umxv , b.mxv );
         if( b.umiv < ret.umiv ) ret.umiv = b.umiv , ret.umxv = b.umxv;
         return ret;
    }
    inline void fill(const int &x) {
        miv = mxv = x , umiv = inf , umxv = -inf;
    }
    inline void apply_add(const lli &x) {
        miv +=x , mxv +=x , umiv += x , umxv += x;
    }
    inline void apply_min(const lli &x) {
        miv = min( miv , x ) , mxv= min( mxv , x );
        if( umiv < x ) umxv = max( umxv , x );
        else umiv = inf , umxv = -inf;
    }
}ns[maxn<<3];

int in[maxn];
int l[maxn<<3],r[maxn<<3],lson[maxn<<3],rson[maxn<<3],cnt;
lli lazy_add[maxn<<3],lazy_min[maxn<<3];

inline void build(int pos,int ll,int rr) {
    l[pos] = ll , r[pos] = rr;
    if( ll == rr ) return ns[pos].fill(in[ll]);
    const int mid = ( ll + rr ) >> 1;
    build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr);
    ns[pos] = ns[lson[pos]] + ns[rson[pos]];
}
inline void apply_add(int pos,const lli &x) {
    lazy_add[pos] += x , lazy_min[pos] += x ,
    ns[pos].apply_add(x);
}
inline void apply_min(int pos,const lli &x) {
    lazy_min[pos] = min( lazy_min[pos] , x ) ,
    ns[pos].apply_min(x);
}
inline void push(int pos) {
    if( lazy_add[pos] ) {
        apply_add(lson[pos],lazy_add[pos]) , apply_add(rson[pos],lazy_add[pos]) ,
        lazy_add[pos] = 0;
    }
    if( lazy_min[pos] < lim ) {
        apply_min(lson[pos],lazy_min[pos]) , apply_min(rson[pos],lazy_min[pos]) ,
        lazy_min[pos] = inf;
    }
}
inline void update_add(int pos,int ll,int rr,const lli &x) {
    if( rr < l[pos] || r[pos] < ll ) return;
    if( ll <= l[pos] && r[pos] <= rr ) return apply_add(pos,x);
    push(pos);
    update_add(lson[pos],ll,rr,x) , update_add(rson[pos],ll,rr,x) ,
    ns[pos] = ns[lson[pos]] + ns[rson[pos]] ;
}
inline void update_min(int pos,int ll,int rr,const lli &x) {
    if( rr < l[pos] || r[pos] < ll ) return;
    if( ll <= l[pos] && r[pos] <= rr ) return apply_min(pos,x);
    push(pos);
    update_min(lson[pos],ll,rr,x) , update_min(rson[pos],ll,rr,x) ,
    ns[pos] = ns[lson[pos]] + ns[rson[pos]];
}
inline Node query(int pos,int ll,int rr) {
    if( ll <= l[pos] && r[pos] <= rr ) return ns[pos];
    push(pos);
    const int mid = ( l[pos] + r[pos] ) >> 1;
    if( rr <= mid ) return query(lson[pos],ll,rr);
    if( ll > mid ) return query(rson[pos],ll,rr);
    const Node ql = query(lson[pos],ll,rr) , qr = query(rson[pos],ll,rr);
    return ql + qr;
}

int main() {
    static int n,m;
    scanf("%d%d",&n,&m) , memset(lazy_min,0x3f,sizeof(lazy_min));
    for(int i=1;i<=n;i++) scanf("%d",in+i);
    build(cnt=1,1,n);
    for(int i=1,o,l,r,x;i<=m;i++) {
        scanf("%d%d%d",&o,&l,&r);
        if( o == 3 ) {
            Node ans = query(1,l,r);
            printf("%d
",ans.umiv<lim?r-l+1:1);
        } else {
            scanf("%d",&x);
            if( o == 1 ) update_add(1,l,r,x);
            else if( o ==2 ) update_min(1,l,r,x);
        }
    }
    return 0;
}