北京集训:20180318

果然我还是太菜了......

T1:

先分解成标准形式，然后每个质因数必须有最高次，然后状压DP?
发现并不可做......
然后写了10分的大力背包走了......
正解是容斥。

然而他的公式挂了......
大概意思就是枚举我们有几个没有到最高次，然后用高维前缀和(积)进行DP。
关于高维前缀和可以看我以前的博客......
为什么考场没想起来......
考场10分代码:

#include<cstdio>
#include<cstring>
//#include<iostream>
//#define debug cout
//using namespace std;
typedef long long int lli;
const int maxn=5e2+1e1,maxk=22;
const int mod=232792561;

lli f[2][maxn][maxk];
int n,k;

inline int gcd(int x,int y) {
    register int t;
    while( t = x % y )
        x = y , y = t;
    return y;
}
inline int lcm(int x,int y) {
    if( ! ( x && y ) ) return x | y;
    return x / gcd(x,y) * y;
}
inline void trans(lli dst[maxn][maxk],const lli sou[maxn][maxk],int now) {
    for(int i=0;i<=n;i++) {
        const int tar = lcm(i,now);
        if( tar > n ) continue;
        for(int j=0;j<k;j++) ( dst[tar][(j+now)%k] += sou[i][j] ) %= mod;
    }
    for(int i=0;i<=n;i++)
        for(int j=0;j<k;j++)
            ( dst[i][j] += sou[i][j] ) %= mod;
}

int main() {
    static int T,cur;
    scanf("%d",&T);
    while(T--) {
        memset(f,0,sizeof(f)) , cur = 0;
        f[cur][0][0] = 1;
        scanf("%d%d",&n,&k);
        for(int i=1;i<=n;i++) {
            cur ^= 1;
            memset(f[cur],0,sizeof(f[1]));
            trans(f[cur],f[cur^1],i);
        }
        printf("%lld
",f[cur][n][0]);
    }
    return 0;
}

正解代码:

//#include<iostream>
#include<cstdio>
#include<cstring>
//#include<algorithm>
//#define debug cout
typedef long long int lli;
//using namespace std;
const int maxl=2e5+1e2,maxd=2e1+1e1,maxp=7e1+1e1;
const int mod=232792561;

int k;
lli wpows[maxd];

inline lli fastpow(lli base,int tim) {
    lli ret = 1;
    while( tim ) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}

struct Poly {
    lli dat[maxd];
    Poly() {
        memset(dat,0,sizeof(dat));
    }
    inline void fill(int x) { // get point value expression , only p ^ x and p ^ 0 is 1 .
        for(int i=0;i<k;i++)
            dat[i] = ( wpows[x*i%k] + 1 ) % mod;
    }
    friend Poly operator + (const Poly &a,const Poly &b) {
        Poly ret;
        for(int i=0;i<k;i++) ret.dat[i] = ( a.dat[i] + b.dat[i] ) % mod;
        return ret;
    }
    friend Poly operator - (const Poly &a,const Poly &b) {
        Poly ret;
        for(int i=0;i<k;i++) ret.dat[i] = ( a.dat[i] - b.dat[i] + mod ) % mod;
        return ret;
    }
    friend Poly operator * (const Poly &a,const Poly &b) {
        Poly ret;
        for(int i=0;i<k;i++) ret.dat[i] = a.dat[i] * b.dat[i] % mod;
        return ret;
    }
    inline lli calc() {
        lli ret = 0;
        for(int i=0;i<k;i++) ( ret += dat[i] ) %= mod;
        ret = ret * fastpow(k,mod-2) % mod;
        return ret;
    }
}f[maxl];

lli dvs[maxd],dvspows[maxd][maxp];
int tim[maxd],facs[maxd];
int cnt,full;

inline void prew() {
    const lli w = fastpow(71,mod/k);
    *wpows = 1;
    for(int i=1;i<k;i++) wpows[i] = wpows[i-1] * w % mod;
}
inline void cut(lli x) {
    for(int i=2;i<=100;i++)
        if( ! ( x % i ) ) {
            dvs[++cnt] = i , dvspows[cnt][0] = 1;
            while( ! ( x % i ) ) {
                ++tim[cnt] ,
                dvspows[cnt][tim[cnt]] = dvspows[cnt][tim[cnt]-1] * i ,
                x /= i;
            }
        }
}
inline void getfac() {
    *facs = 1;
    for(int i=1;i<=cnt;i++) facs[i] = facs[i-1] * ( tim[i] + 1 );
}
inline lli getnum(int id) { // access as high-dimension array .
    lli ret = 1;
    for(int i=1;i<=cnt;i++) ret *= dvspows[i][id%facs[i]/facs[i-1]];
    return ret;
}
inline void dp() {
    for(int j=1;j<=cnt;j++)
        for(int i=0;i<full;i++)
            if( i % facs[j] / facs[j-1] )
                f[i] = f[i] * f[i-facs[j-1]];
}
inline Poly getans() {
    Poly ret;
    for(int sta=0;sta<(1<<cnt);sta++) {
        int sg = 1 , now = full - 1;
        for(int i=1;i<=cnt;i++) if( sta & ( 1 << ( i - 1 ) ) ) {
            sg *= -1 , now -= facs[i-1];
        }
        if( sg == 1 ) ret = ret + f[now];
        else ret = ret - f[now];
    }
    return ret;
}
inline void init() {
    memset(tim,0,sizeof(tim)) , cnt = 0;
    memset(f,0,sizeof(f));
}

int main() {
    static int T;
    static lli n;
    scanf("%d",&T);
    while(T--) {
        scanf("%lld%d",&n,&k) , init() , prew();
        cut(n) , getfac() , full = facs[cnt];
        for(int i=0;i<full;i++) {
            lli now = getnum(i);
            f[i].fill(now%k);
        }
        dp();
        Poly ans = getans();
        printf("%lld
",ans.calc());
    }
    return 0;
}

T2:

显然是个反演+杜教筛......
三个gcd很不好办啊，拆了他也不好做，不如留着，万一大力出奇迹了呢......

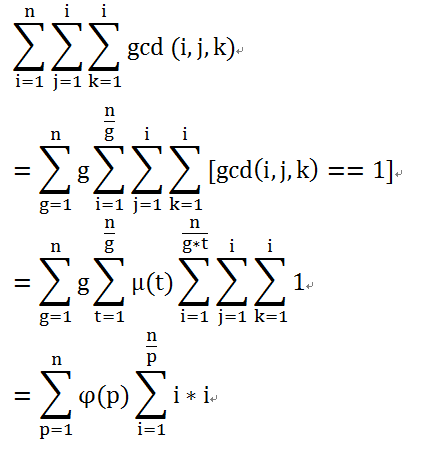
前面是μ*id=φ，后面是x^2的前缀和，显然可以背过......
话说考场如果背不过怎么办呢?显然他是一个k+1次多项式，然后我们可以拉格朗日插值......
官方题解感觉推傻了......

考场AC代码:

//#include<iostream>
#include<cstdio>
//#include<cstring>
//#include<algorithm>
//#define debug cout
typedef long long int lli;
//using namespace std;
const int maxn=1e6+1e2,lim=1e6;

lli phi[maxn],mem[maxn],vis[maxn];
int n,mod,inv;

inline lli fastpow(lli base,int tim) {
    lli ret = 1;
    while( tim ) {
        if( tim & 1 ) ret = ret * base % mod;
        if( tim >>= 1 ) base = base * base % mod;
    }
    return ret;
}

inline void sieve() {
    static int vis[maxn],prime[maxn],cnt;
    phi[1] = 1;
    for(int i=2;i<=lim;i++) {
        if( !vis[i] ) prime[++cnt] = i , phi[i] = i - 1;
        for(int j=1;j<=cnt&&(lli)i*prime[j]<=lim;j++) {
            const int tar = i * prime[j];
            vis[tar] = 1; 
            if( i % prime[j] ) phi[tar] = phi[i] * ( prime[j] - 1 );
            else {
                phi[tar] = phi[i] * prime[j];
                break;
            }
        }
    }
    for(int i=1;i<=lim;i++) ( phi[i] += phi[i-1] ) %= mod;
}

inline lli sumphi(lli x) {
    if( x <= lim )
        return phi[x];
    lli mp = n / x;
    if( vis[mp] )
        return mem[mp];
    lli ret = ( (lli) x ) * ( x + 1 ) >> 1;
    for(lli i=2,j;i<=x;i=j+1) {
        j = x / ( x / i );
        ret -= ( j - i + 1 ) * sumphi( x / i );
    }
    vis[mp] = 1;
    return mem[mp] = ret;
}

inline lli sum(lli x) {
    return x * ( x + 1 ) % mod * ( ( 2 * x + 1 ) % mod ) % mod * inv % mod;
}
inline lli segphi(lli l,lli r) {
    return ( sumphi(r) - sumphi(l-1) + mod ) % mod;
}
inline lli calc(lli n) {
    lli ret = 0;
    for(lli i=1,j;i<=n;i=j+1) {
        j = n / ( n / i );
        ( ret += segphi(i,j) * sum( n / i ) % mod ) %= mod;
    }
    return ret;
}

int main() {
    scanf("%d%d",&n,&mod) , sieve();
    inv = fastpow(6,mod-2);
    printf("%lld
",calc(n));
    return 0;
}

T3:

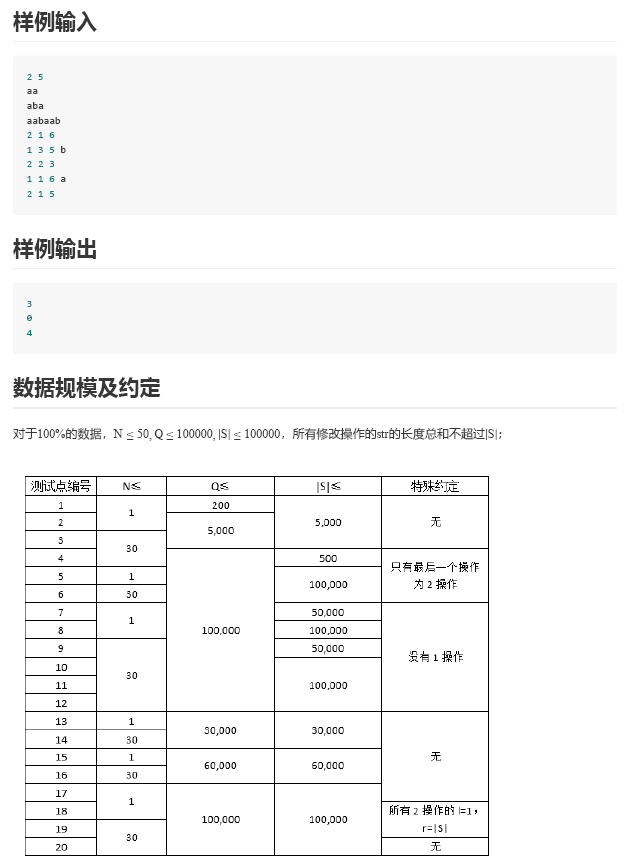
字符串题，没时间了，写个20分暴力走了。
woc暴力怎么又WA了?
题解:

考场零分暴力:

//#include<iostream>
#include<cstdio>
#include<cstring>
//#include<algorithm>
#include<queue>
//#define debug cout
typedef long long int lli;
//using namespace std;
const int maxn=1e2+1e1,maxq=1e5+1e2;

struct ACautomatic {
    int ch[maxn][26],fail[maxn],deg[maxn],sum[maxn],tim[maxn],root,cnt;
    ACautomatic() { root = ++cnt; }
    inline void insert(char* s,int li) {
        int now = root;
        for(int i=1;i<=li;i++) {
            const int t = s[i] - 'a';
            if( !ch[now][t] ) ch[now][t] = ++cnt;
            now = ch[now][t];
        }
        //debug<<"now = "<<now<<endl;
        ++sum[now];
    }
    inline void buildfail() {
        std::queue<int> q;
        for(int i=0;i<26;i++)
            if( !ch[root][i] ) ch[root][i] = i;
            else fail[ch[root][i]] = root , q.push(ch[root][i]);
        while( q.size() ) {
            const int pos = q.front(); q.pop();
            for(int i=0;i<26;i++)
                if( !ch[pos][i] ) ch[pos][i] = ch[fail[pos]][i];
                else fail[ch[pos][i]] = ch[fail[pos]][i] , q.push(ch[pos][i]);
        }
    }
    inline void pir(char* s,int li) {
        int now = root;
        for(int i=0;i<li;i++) {
            const int t = s[i] - 'a';
            //debug<<"now = "<<now<<endl;
            now = ch[now][t] , ++tim[now];
        }
    }
    inline lli calc() {
        lli ret = 0;
        std::queue<int> q;
        for(int i=1;i<=cnt;i++) if( fail[i] ) ++deg[fail[i]];
        for(int i=1;i<=cnt;i++) if( !deg[i] ) q.push(i);
        while( q.size() ) {
            const int pos = q.front(); q.pop();
            if( pos == root ) continue;
            ret += (lli) tim[pos] * sum[pos];
            tim[fail[pos]] += tim[pos];
            if( !--deg[fail[pos]] ) q.push(fail[pos]);
        }
        return ret;
    }
    inline void rtq() {
        memset(deg,0,sizeof(deg)) , memset(tim,0,sizeof(tim));
    }
}AC;

char in[maxq],tp[maxq];

int main() {
    static int n,q,li;
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++) {
        scanf("%s",tp+1) , li = strlen(tp+1);
        AC.insert(tp,li);
    }
    AC.buildfail();
    scanf("%s",in+1);
    for(int i=1,o,l,r;i<=q;i++) {
        scanf("%d%d%d",&o,&l,&r);
        if( o == 2 ) {
            AC.rtq();
            AC.pir(in+l,r-l+1);
            printf("%lld
",AC.calc());
        } else {
            scanf("%s",tp) , li = strlen(tp);
            for(int j=0;j<r-l+1;j++)
                in[l+j] = tp[j%li];
        }
    }
    return 0;
}

标程:

#include<bits/stdc++.h>
#define ALPHA 27
#define N 55
#define M 100005
#define pii pair<int,int>
#define mp(x,y) make_pair(x,y)
#define fr first
#define se second 
using namespace std;
namespace AC{
    int ne[M][ALPHA],fail[M],val[M],cnt,root;//0~cnt-1
    void insert(int &k,char *s,int len){
        if(k==0) k=++cnt;
        if(len!=0) insert(ne[k][s[0]-'a'],s+1,len-1);
        else val[k]++;
    }
    void buildAC(){
        fail[root]=root;queue<int> q;
        for(int i=0;i<26;i++)
            if(ne[root][i]==0) ne[root][i]=root;
            else fail[ne[root][i]]=root,q.push(ne[root][i]);
        while(!q.empty()){
            int u=q.front();q.pop();
            for(int i=0;i<26;i++){
                int &v=ne[u][i];
                if(v==0) v=ne[fail[u]][i];
                else fail[v]=ne[fail[u]][i],q.push(v),val[v]+=val[fail[v]];
            }
        }
    }
}
 
struct msg{
    int st[N],ans[N];
    pii query(pii x){
        return mp(st[x.fr],x.se+ans[x.fr]);
    }
    void merge(const msg &b){
        for(int i=0;i<AC::cnt;i++) ans[i]+=b.ans[st[i]],st[i]=b.st[st[i]];
    }
    void ini(){
        for(int i=0;i<AC::cnt;i++) st[i]=i,ans[i]=0;
    }
    void inital(char ch){
        for(int i=0;i<AC::cnt;i++) st[i]=AC::ne[i+1][ch-'a']-1,ans[i]=AC::val[st[i]+1];
    }
};
msg ne[M*19];
#define gid(pos,pw) ((pos)*18+(pw))
char str[M];int len,lenth[M],li[M],ri[M],idcnt;
void prework(int l,int r,int d){
    int mlen=(r-l+1);
    for(int i=l;i<=r;i++) ne[gid(i,0)].inital(str[i]);
    for(int i=1;(1<<i)<=d;i++)
        for(int j=l;j<=r;j++)
            ne[gid(j,i)]=ne[gid(j,i-1)],ne[gid(j,i)].merge(ne[gid((j-l+(1<<(i-1)))%mlen+l,i-1)]);
}
 
namespace SGT{
    struct xds{
        int pw;
        msg x;
        int tagid,pos;
    }a[(1<<18)+3];int cnt;
    inline void addmark(int k,int id,int pos){
        a[k].x=ne[gid(li[id]+pos,a[k].pw)];
        a[k].tagid=id;a[k].pos=pos;
    }
    inline void pushdown(int k){
        if(a[k].tagid==0||a[k].pw==0) return;
        addmark(k<<1,a[k].tagid,a[k].pos);
        int npos=(a[k].pos+(1<<(a[k].pw-1)))%lenth[a[k].tagid];
        addmark(k<<1|1,a[k].tagid,npos);
        a[k].tagid=0;a[k].pos=0;
    }
    inline void update(int k){
        a[k].x=a[k<<1].x;
        a[k].x.merge(a[k<<1|1].x);
    }
    void build(int k,int l,int r,char *s,int pw){
        a[k].pw=pw;
        if(l==r){
            a[k].x.inital(s[l]);return;
        }else{
            int mid=(l+r)>>1;
            build(k<<1,l,mid,s,pw-1);
            build(k<<1|1,mid+1,r,s,pw-1);
            update(k);
        }
    }
    pii query(int k,int l,int r,pii input,int nl,int nr){
        if(nl==l&&nr==r) return a[k].x.query(input);
        pushdown(k);
        int mid=(nl+nr)>>1;
        if(l>mid) return query(k<<1|1,l,r,input,mid+1,nr);
        else if(r<=mid) return query(k<<1,l,r,input,nl,mid);
        return query(k<<1|1,mid+1,r,query(k<<1,l,mid,input,nl,mid),mid+1,nr);
    }
    void modify(int k,int l,int r,int id,int st,int nl,int nr){
        if(nl==l&&nr==r){
            addmark(k,id,st);
        }else{
            pushdown(k);
            int mid=(nl+nr)>>1;
            if(l>mid) modify(k<<1|1,l,r,id,st,mid+1,nr);
            else if(r<=mid) modify(k<<1,l,r,id,st,nl,mid);
            else modify(k<<1,l,mid,id,st,nl,mid),modify(k<<1|1,mid+1,r,id,(st+mid-l+1)%lenth[id],mid+1,nr);
            update(k);
        }
    }
}
 
char s[(1<<18)+3],Ti[N];
int n,m,q,pwlen;
void readin(){
    //cerr<<(sizeof(ne)+sizeof(SGT::a))/1024/1024<<endl;
    memset(s,'a',sizeof(s));
    scanf("%d%d",&n,&q);
    for(int i=1;i<=n;i++) scanf("%s",Ti),AC::insert(AC::root,Ti,strlen(Ti));
    scanf("%s",s+1);
    m=strlen(s+1);
    s[m+1]='a';
}
void solve(){
    for(int i=1;i<=q;i++){
        int op,l,r;
        scanf("%d%d%d",&op,&l,&r);
        if(op==1){
            scanf("%s",str+len);idcnt++;
            li[idcnt]=len;len+=strlen(str+len);ri[idcnt]=len-1;
            lenth[idcnt]=ri[idcnt]-li[idcnt]+1;
            prework(li[idcnt],ri[idcnt],r-l+1);
            SGT::modify(1,l,r,idcnt,0,1,(1<<pwlen));
        }else{
            pii ret=mp(0,0);
            ret=SGT::query(1,l,r,ret,1,(1<<pwlen));
            printf("%d
",ret.se);
        }
    }
    if(len>100000) {puts("Invaid Input2");return;}
}
int main(){
     
    readin();
    AC::buildAC();
    if(AC::cnt>50) return puts("Invaid Input1"),0;
    for(pwlen=0;(1<<pwlen)<m;pwlen++);
    SGT::build(1,1,(1<<pwlen),s,pwlen);
    solve();
    return 0;
}