考试对于蒟蒻而言简直就是灾难......
T1:


又是一道组合数学神题。
显然这张图会由n个环组成,我们考虑在每个环内分别选>=1个点,最后点总方案的乘积就是在这些环中选k个点的答案。
怎么计算呢?我们可以f[i][j]表示前i个环,选j个点的方案数。转移就是f[i][j]=f[i-1][j-p]*C(siz[i],p)(0<=p<=siz[i])。
答案就是f[len][k]了。
这样大力背包就有50分。
显然这个转移是一个卷积。如果我们用NTT去优化的话就有65分了。
我呢?写了NTT结果提交没注释freopen,爆零了啊......
正解就是这样,只不过优化了一下顺序:
如果我们采用启发式NTT合并的话,可以把复杂度降低到nlog^2n。
(其实我也想到把这些生成函数卷积起来而不是背包,只是没想到启发式QAQ)
大力背包代码:

#include<iostream> #include<cstdio> #include<cstring> #include<algorithm> #define debug cout typedef long long int lli; using namespace std; const int maxn=5.3e4,maxe=2.6e3,lim=52501; const int mod=998244353; lli fac[maxn],inv[maxn]; int in[maxn]; int dfn[maxn],low[maxn],bel[maxn],siz[maxn],dd,iid; int stk[maxn],ins[maxn],vis[maxn],top; lli f[2][maxn]; int n,full; inline lli fastpow(lli base,int tim) { lli ret = 1; while( tim ) { if( tim & 1 ) ret = ret * base % mod; if( tim >>= 1 ) base = base * base % mod; } return ret % mod; } inline void sieve() { *fac = 1; for(int i=1;i<=lim;i++) fac[i] = fac[i-1] * i % mod; inv[lim] = fastpow(fac[lim],mod-2); for(int i=lim;i;i--) inv[i-1] = inv[i] * i % mod; } inline lli c(int n,int m) { return fac[n] * inv[m] % mod * inv[n-m] % mod; } inline void tarjan(int pos) { vis[pos] = 1 , low[pos] = dfn[pos] = ++dd; stk[++top] = pos , ins[pos] = 1; if( !vis[in[pos]] ) { tarjan(in[pos]) , low[pos] = min( low[pos] , low[in[pos]] ); } else if( ins[in[pos]] ) low[pos] = min( low[pos] , dfn[in[pos]] ); if( low[pos] == dfn[pos] ) { ++iid; do { const int x = stk[top--]; ins[x] = 0; bel[x] = iid , ++siz[iid]; } while( ins[pos] ); } } inline lli calc() { // There can't be any chain ! memset(f,0,sizeof(f)) , **f = 1; int cur = 0 , fs = 0; for(int i=1;i<=iid;i++) { fs += siz[i] , cur ^= 1; memset(f[cur],0,sizeof(f[cur])); for(int j=1;j<=fs&&j<=full;j++) // j means full size . for(int k=1;k<=siz[i]&&k<=j;k++) { // k means person in ring[i] f[cur][j] += f[cur^1][j-k] * c(siz[i],k) % mod , f[cur][j] %= mod; } for(int j=0;j<i;j++) f[cur][j] = 0; } return f[cur][full]; } inline void reset() { memset(vis,0,sizeof(vis)) , memset(siz,0,sizeof(siz)) , dd = iid = 0; } int main() { static int T; scanf("%d",&T) , sieve(); while(T--) { scanf("%d%d",&n,&full) , reset(); for(int i=1;i<=n;i++) scanf("%d",in+i); for(int i=1;i<=n;i++) if( !vis[i] ) tarjan(i); printf("%lld ",calc()*fastpow(c(n,full),mod-2)%mod); } return 0; }
爆零NTT代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define debug cout 6 typedef long long int lli; 7 using namespace std; 8 const int maxn=5.3e4,lim=52501; 9 const int mod=998244353,g=3; 10 11 lli fac[maxn],inv[maxn]; 12 int in[maxn]; 13 int dfn[maxn],low[maxn],bel[maxn],siz[maxn],dd,iid; 14 int stk[maxn],ins[maxn],vis[maxn],top; 15 lli f[2][maxn<<4],tmp[maxn<<4]; 16 int n,full; 17 18 inline lli fastpow(lli base,int tim) { 19 lli ret = 1; 20 while( tim ) { 21 if( tim & 1 ) ret = ret * base % mod; 22 if( tim >>= 1 ) base = base * base % mod; 23 } 24 return ret % mod; 25 } 26 inline void sieve() { 27 *fac = 1; 28 for(int i=1;i<=lim;i++) fac[i] = fac[i-1] * i % mod; 29 inv[lim] = fastpow(fac[lim],mod-2); 30 for(int i=lim;i;i--) inv[i-1] = inv[i] * i % mod; 31 } 32 inline lli c(int n,int m) { 33 return fac[n] * inv[m] % mod * inv[n-m] % mod; 34 } 35 inline void tarjan(int pos) { 36 vis[pos] = 1 , low[pos] = dfn[pos] = ++dd; 37 stk[++top] = pos , ins[pos] = 1; 38 if( !vis[in[pos]] ) { 39 tarjan(in[pos]) , 40 low[pos] = min( low[pos] , low[in[pos]] ); 41 } else if( ins[in[pos]] ) low[pos] = min( low[pos] , dfn[in[pos]] ); 42 if( low[pos] == dfn[pos] ) { 43 ++iid; 44 do { 45 const int x = stk[top--]; ins[x] = 0; 46 bel[x] = iid , ++siz[iid]; 47 } while( ins[pos] ); 48 } 49 } 50 51 inline void NTT(lli* dst,int n,int ope) { 52 for(int i=0,j=0;i<n;i++) { 53 if( i < j ) swap( dst[i] , dst[j] ); 54 for(int t=n>>1;(j^=t)<t;t>>=1) ; 55 } 56 for(int len=2;len<=n;len<<=1) { 57 const int h = len >> 1; 58 lli per = fastpow(g,mod/(len)); 59 if( !~ope ) per = fastpow(per,mod-2); 60 for(int st=0;st<n;st+=len) { 61 lli w = 1; 62 for(int pos=0;pos<h;pos++) { 63 const lli u = dst[st+pos] , v = dst[st+pos+h] * w % mod; 64 dst[st+pos] = ( u + v ) % mod , 65 dst[st+pos+h] = ( u - v + mod ) % mod , 66 w = w * per % mod; 67 } 68 } 69 } 70 if( !~ope ) { 71 const lli mul = fastpow(n,mod-2); 72 for(int i=0;i<n;i++) dst[i] = dst[i] * mul % mod; 73 } 74 } 75 inline void trans(lli* dst,lli* sou1,lli* sou2,int full,int n) { 76 int len; 77 for(len=1;len<=((full+n)<<1);len<<=1); 78 len <<= 1; 79 for(int i=0;i<len;i++) sou2[i] = 0; 80 for(int i=1;i<=min(full,n);i++) sou2[i] = c(full,i); 81 NTT(sou1,len,1) , NTT(sou2,len,1); 82 for(int i=0;i<len;i++) dst[i] = sou1[i] * sou2[i] % mod; 83 NTT(dst,len,-1); 84 } 85 inline lli calc() { // There can't be any chain ! 86 memset(f,0,sizeof(f)) , **f = 1; 87 int cur = 0 , fs = 0; 88 for(int i=1;i<=iid;i++) { 89 fs += siz[i] , cur ^= 1; 90 memset(f[cur],0,sizeof(f[cur])); 91 trans(f[cur],f[cur^1],tmp,siz[i],min(full,fs)); 92 for(int j=0;j<i;j++) f[cur][j] = 0; 93 } 94 return f[cur][full]; 95 } 96 97 inline void reset() { 98 memset(vis,0,sizeof(vis)) , memset(siz,0,sizeof(siz)) , 99 dd = iid = 0; 100 } 101 102 int main() { 103 static int T; 104 scanf("%d",&T) , sieve(); 105 while(T--) { 106 scanf("%d%d",&n,&full) , reset(); 107 for(int i=1;i<=n;i++) scanf("%d",in+i); 108 for(int i=1;i<=n;i++) if( !vis[i] ) tarjan(i); 109 printf("%lld ",calc()*fastpow(c(n,full),mod-2)%mod); 110 } 111 return 0; 112 }
正解代码:

1 #pragma GCC optimize("Ofast,no-stack-protector") 2 #pragma GCC optimize("-funsafe-loop-optimizations") 3 #pragma GCC optimize("-funroll-loops") 4 #pragma GCC optimize("-fwhole-program") 5 #include<iostream> 6 #include<cstdio> 7 #include<cstring> 8 #include<algorithm> 9 #include<vector> 10 #include<queue> 11 #define debug cout 12 typedef long long int lli; 13 using namespace std; 14 const int maxn=152510,maxl=524288,lim=152501; 15 const int mod=998244353,g=3; 16 17 int in[maxn],vis[maxn],siz[maxn],len; 18 lli fac[maxn],inv[maxn],ta[maxl],tb[maxl],tm[maxl]; 19 vector<lli> vec[maxn]; 20 priority_queue<pair<int,int> > pq; 21 int n; 22 23 inline int findring(int pos,int ret) { 24 if( vis[pos] ) return ret; 25 vis[pos] = 1; 26 return findring(in[pos],ret+1); 27 } 28 inline lli fastpow(lli base,int tim) { 29 lli ret = 1; 30 while (tim) { 31 if ( tim & 1 ) ret = ret * base % mod; 32 if( tim >>= 1 ) base = base * base % mod; 33 } 34 return ret; 35 } 36 inline void NTT(lli* dst,int n,int tpe) { 37 for(int i=0,j=0;i<n;i++) { 38 if( i < j ) swap(dst[i],dst[j]); 39 for(int t=n>>1;(j^=t)<t;t>>=1) ; 40 } 41 for(int len=2;len<=n;len<<=1) { 42 const int h = len >> 1; 43 lli per = fastpow(g,mod/len); 44 if( !~tpe ) per = fastpow(per,mod-2); 45 for(int st=0;st<n;st+=len) { 46 lli w = 1; 47 for(int pos=0;pos<h;pos++) { 48 const lli u = dst[st+pos] , v = dst[st+pos+h] * w % mod; 49 dst[st+pos] = ( u + v ) % mod , 50 dst[st+pos+h] = ( u - v + mod ) % mod , 51 w = w * per % mod; 52 } 53 } 54 } 55 if( !~tpe ) { 56 const lli mul = fastpow(n,mod-2); 57 for(int i=0;i<n;i++) dst[i] = dst[i] * mul % mod; 58 } 59 } 60 inline void sieve() { 61 *fac = 1; 62 for(int i=1;i<=lim;i++) fac[i] = fac[i-1] * i % mod; 63 inv[lim] = fastpow(fac[lim],mod-2); 64 for(int i=lim;i;i--) inv[i-1] = inv[i] * i % mod; 65 } 66 inline lli c(int n,int m) { 67 return fac[n] * inv[m] % mod * inv[n-m] % mod; 68 } 69 inline void merge(vector<lli> &a,vector<lli> &b) { // merge a and b into a . 70 int len,ns=a.size()+b.size()-1; 71 for(len=1;len<=ns;len<<=1) ; 72 for(int i=0;i<len;i++) ta[i] = tb[i] = tm[i] = 0; 73 for(unsigned i=0;i<a.size();i++) ta[i] = a[i]; 74 for(unsigned i=0;i<b.size();i++) tb[i] = b[i]; 75 NTT(ta,len,1) , NTT(tb,len,1); 76 for(int i=0;i<len;i++) tm[i] = ta[i] * tb[i] % mod; 77 NTT(tm,len,-1); 78 a.resize(ns); 79 for(int i=0;i<ns;i++) a[i] = tm[i]; 80 } 81 inline int getans() { 82 while( pq.size() != 1 ) { 83 const int a = pq.top().second; pq.pop(); 84 const int b = pq.top().second; pq.pop(); 85 merge(vec[a],vec[b]); 86 pq.push(make_pair(-(vec[a].size()-1),a)); 87 } 88 int ret = pq.top().second; pq.pop(); 89 return ret; 90 } 91 inline void pre() { 92 for(int i=1;i<=len;i++) { 93 vec[i].resize(siz[i]+1); 94 for(int j=1;j<=siz[i];j++) vec[i][j] = c(siz[i],j); 95 pq.push(make_pair(-(vec[i].size()-1),i)); 96 } 97 } 98 inline void getring() { 99 memset(vis,0,sizeof(vis)) , len = 0; 100 for(int i=1;i<=n;i++) if( !vis[i] ) siz[++len] = findring(i,0); 101 } 102 103 int main() { 104 static int T,full,p; 105 scanf("%d",&T) , sieve(); 106 while(T--) { 107 scanf("%d%d",&n,&full); 108 for(int i=1;i<=n;i++) scanf("%d",in+i); 109 getring() , pre(); 110 p = getans(); 111 printf("%lld ",vec[p][full]*fastpow(c(n,full),mod-2)%mod); 112 } 113 return 0; 114 }
T2:
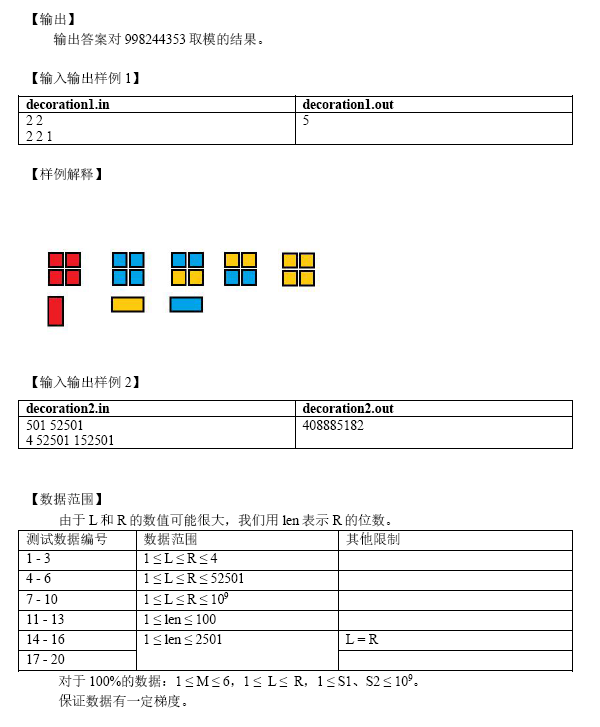
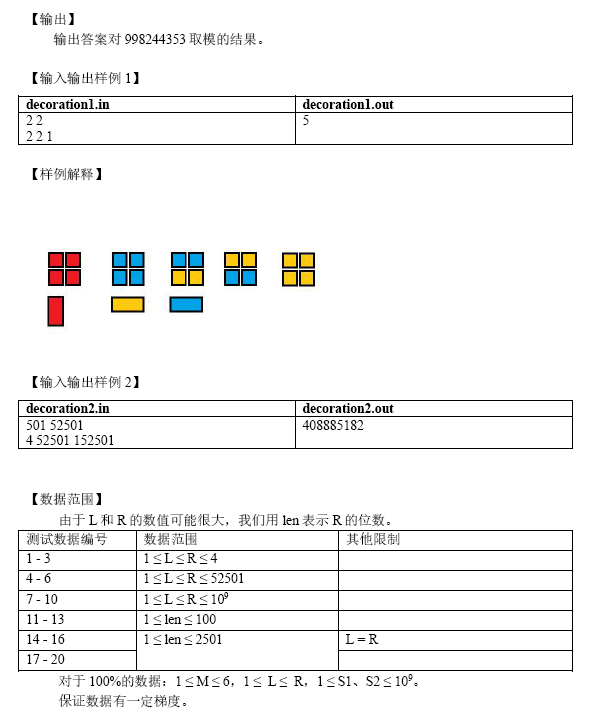
m只有6,显然状压。
转移方式相同,显然矩乘。
答案统计一个前缀和的东西,显然还是矩乘,这样就是矩乘套矩乘了......
然后发现次数很大,不会做,怎么办?
手打了一个高精,又写了一个用欧拉定理降次的程序,排不上。
发现欧拉定理并不适用,就把高精交上去了,拿了60分。
后来发现如果大力取模phi(p)*2降次的话有65分的......
正解是这样的东西,然而并不会......

考场60分代码:

1 #include<bits/stdc++.h> 2 #define debug cout 3 typedef long long int lli; 4 using namespace std; 5 const int maxn=70,maxl=10,maxe=2.6e3+1e2; 6 const int mod=998244353,phi=mod-1; 7 8 int lim; 9 struct Matrix { 10 lli dat[maxn][maxn]; 11 Matrix(int tpe=0) { 12 memset(dat,0,sizeof(dat)); 13 if( tpe ) for(int i=0;i<lim;i++) dat[i][i] = 1; 14 } 15 friend Matrix operator * (const Matrix &a,const Matrix &b) { 16 Matrix ret; 17 for(int i=0;i<lim;i++) 18 for(int j=0;j<lim;j++) 19 for(int k=0;k<lim;k++) 20 ( ret.dat[i][j] += a.dat[i][k] * b.dat[k][j] % mod ) %= mod; 21 return ret; 22 } 23 friend Matrix operator + (const Matrix &a,const Matrix &b) { 24 Matrix ret; 25 for(int i=0;i<lim;i++) 26 for(int j=0;j<lim;j++) 27 ret.dat[i][j] = ( a.dat[i][j] + b.dat[i][j] ) % mod; 28 return ret; 29 } 30 inline void print() { 31 for(int i=0;i<lim;i++) { 32 for(int j=0;j<lim;j++) debug<<setw(3)<<dat[i][j]<<" "; 33 debug<<endl; 34 } 35 } 36 }mtrans,mini; 37 38 struct MatrixMatrix { 39 Matrix dat[2][2]; 40 friend MatrixMatrix operator * (const MatrixMatrix &a,const MatrixMatrix &b) { 41 MatrixMatrix ret; 42 for(int i=0;i<2;i++) 43 for(int j=0;j<2;j++) 44 for(int k=0;k<2;k++) 45 ret.dat[i][j] = ret.dat[i][j] + a.dat[i][k] * b.dat[k][j]; 46 return ret; 47 } 48 }ini,trans,ansl,ansr; 49 50 struct BigInt { 51 int dat[maxe],len; 52 inline void in(const char* s) { // s starts from 0 . 53 len = strlen(s); 54 for(int i=0;i<len;i++) dat[i] = s[len-i-1] - '0'; 55 } 56 inline bool andone() { 57 return dat[0] & 1; 58 } 59 inline void shr() { 60 for(int i=len-1;~i;i--) { 61 dat[i-1] += 10 * ( dat[i] & 1 ) , 62 dat[i] >>= 1; 63 } 64 while( len && !dat[len-1] ) --len; 65 } 66 inline bool iszero() { 67 return len == 0; 68 } 69 inline void minusone() { 70 --dat[0]; 71 for(int i=0;i<len;i++) 72 if( dat[i] < 0 ) dat[i] += 10 , dat[i+1]--; 73 while( len && !dat[len-1] ) --len; 74 } 75 }l,r; 76 77 bool vis[maxl],nxt[maxl]; 78 int s1,s2,m; 79 lli ans; 80 81 inline int zip() { 82 int ret = 0; 83 for(int i=0;i<6;i++) 84 ret += ( (int) nxt[i] << i ); 85 return ret; 86 } 87 inline void unzip(int sta) { 88 for(int i=0;i<m;i++) 89 vis[i] = ( sta >> i ) & 1; 90 } 91 inline void dfs(int pos,int sou,lli ways) { 92 if( pos == m ) { 93 ( mtrans.dat[sou][zip()] += ways ) %= mod; 94 return; 95 } 96 if( vis[pos] ) return dfs(pos+1,sou,ways); 97 else { 98 vis[pos] = nxt[pos] = 1; 99 dfs(pos+1,sou,ways*s1%mod); 100 vis[pos] = nxt[pos] = 0; 101 if( pos != m-1 && !vis[pos+1] ) { 102 vis[pos] = vis[pos+1] = 1; 103 dfs(pos+1,sou,ways*s2%mod); 104 vis[pos] = vis[pos+1] = 0; 105 } 106 } 107 } 108 109 inline MatrixMatrix fastpow(MatrixMatrix base,BigInt tim) { 110 MatrixMatrix ret = ini; 111 while(!tim.iszero()) { 112 if( tim.andone() ) ret = ret * base; 113 base = base * base , tim.shr(); 114 } 115 return ret; 116 } 117 118 inline void init() { 119 lim = 1 << m; 120 for(int i=0;i<lim;i++) { 121 unzip(i); 122 dfs(0,i,1); 123 } 124 mini.dat[0][0] = 1; 125 ini.dat[0][0] = ini.dat[0][1] = mini; 126 trans.dat[0][0] = trans.dat[0][1] = mtrans , trans.dat[1][1] = Matrix(1); 127 } 128 129 inline void readin() { 130 static char buf[5002]; 131 scanf("%s",buf) , l.in(buf); 132 scanf("%s",buf) , r.in(buf); 133 l.minusone(); 134 } 135 136 int main() { 137 readin(); 138 scanf("%d%d%d",&m,&s1,&s2); 139 init(); 140 ansl = fastpow(trans,l) , ansr = fastpow(trans,r); 141 ans = ( ansr.dat[0][1].dat[0][0] - ansl.dat[0][1].dat[0][0] + mod ) % mod; 142 printf("%lld ",ans); 143 return 0; 144 }
本蒟蒻后来去补了正解,无非就是特征多项式优化矩乘。
我们可以先大力NTT+高斯消元求出矩阵的特征多项式,然后求出期望次数对多项式取模得到的多项式。
预处理转移矩阵的次方,之后的问题就很简单了。
然而由于OJ过于卡常并不能AC,最多85分......
即使是优化取模并加了达夫机器也无力回天......
80分的正常向版本:

1 #pragma GCC optimize(3) 2 #include<bits/stdc++.h> 3 #define debug cout 4 typedef long long int lli; 5 using namespace std; 6 const int maxn=70,maxl=10,maxe=2.6e3+1e2; 7 const int mod=998244353,g=3; 8 9 inline lli fastpow(lli base,int tim) { 10 lli ret = 1; 11 while( tim ) { 12 if( tim & 1 ) ret = ret * base % mod; 13 if( tim >>= 1 ) base = base * base % mod; 14 } 15 return ret; 16 } 17 int lim; 18 struct Matrix { 19 lli dat[maxn<<1][maxn<<1]; 20 Matrix(int tpe=0) { 21 memset(dat,0,sizeof(dat)); 22 if( tpe ) for(int i=0;i<lim;i++) dat[i][i] = 1; 23 } 24 friend Matrix operator * (const Matrix &a,const Matrix &b) { 25 Matrix ret; 26 for(int i=0;i<lim<<1;i++) 27 for(int j=0;j<lim<<1;j++) 28 for(int k=0;k<lim<<1;k++) 29 ( ret.dat[i][j] += a.dat[i][k] * b.dat[k][j] % mod ) %= mod; 30 return ret; 31 } 32 friend Matrix operator + (const Matrix &a,const Matrix &b) { 33 Matrix ret; 34 for(int i=0;i<lim<<1;i++) 35 for(int j=0;j<lim<<1;j++) 36 ret.dat[i][j] = ( a.dat[i][j] + b.dat[i][j] ) % mod; 37 return ret; 38 } 39 friend Matrix operator * (const Matrix &a,const lli &b) { 40 Matrix ret; 41 for(int i=0;i<lim<<1;i++) 42 for(int j=0;j<lim<<1;j++) 43 ret.dat[i][j] = a.dat[i][j] * b % mod; 44 return ret; 45 } 46 inline lli pointval(const lli &x) { 47 const int len = lim << 1; 48 lli ret = 1; 49 for(int i=0;i<len;i++) dat[i][i] = ( dat[i][i] - x % mod + mod ) % mod; 50 //debug<<"x = "<<x<<"muled = "<<endl;print(); 51 for(int i=0;i<len;i++) { 52 int pos = -1; 53 for(int j=i;j<len;j++) if( dat[j][i] ) { 54 pos = j; 55 break; 56 } 57 if( !~pos ) return 0; 58 if( pos != i ) { 59 ret = mod - ret; 60 for(int k=0;k<len;k++) swap( dat[i][k] , dat[pos][k] ); 61 pos = i; 62 } 63 const lli mul = fastpow(dat[i][i],mod-2); 64 ret = ret * dat[i][i] % mod; 65 for(int k=0;k<len;k++) dat[i][k] = dat[i][k] * mul % mod; 66 for(int j=0;j<len;j++) if( dat[j][i] && j != i ) { 67 const lli mul = dat[j][i]; 68 for(int k=0;k<len;k++) dat[j][k] = ( dat[j][k] - dat[i][k] * mul % mod + mod ) % mod; 69 } 70 } 71 //debug<<"ret = "<<ret<<endl; 72 return ret; 73 } 74 inline void print() { 75 for(int i=0;i<lim<<1;i++) { 76 for(int j=0;j<lim<<1;j++) debug<<setw(3)<<dat[i][j]<<" "; 77 debug<<endl; 78 } 79 } 80 }mtrans,mini,trans,ini,tmp,pows[maxn<<1]; 81 82 struct Poly { 83 lli dat[maxn<<2]; 84 Poly(int tpe = 0) { 85 memset(dat,0,sizeof(dat)); 86 *dat = tpe; 87 } 88 lli& operator [] (const int &x) { 89 return dat[x]; 90 } 91 const lli& operator [] (const int &x) const { 92 return dat[x]; 93 } 94 friend Poly operator * (const Poly &a,const Poly &b) { 95 Poly ret; 96 for(int i=0;i<lim<<1;i++) 97 for(int j=0;j<lim<<1;j++) 98 ( ret[i+j] += a[i] * b[j] % mod ) %= mod; 99 //debug<<"muted ret = "; ret.print(); 100 return ret; 101 } 102 friend Poly operator % (const Poly &a,const Poly &b) { 103 Poly ret = a; 104 //debug<<"inital ret = "; ret.print(); 105 //debug<<"inital mod = "; b.print(); 106 int lst = lim << 1; 107 while( lst && !b[lst] ) --lst; 108 //debug<<"lst = "<<lst<<endl; 109 if( !lst ) throw "Moding Zero"; 110 for(int i=(lim<<2)-1;i>=lst;i--) if( ret[i] ) { 111 //debug<<"i = "<<i<<endl; 112 const int mul = ret[i] * fastpow(b[lst],mod-2) % mod; 113 for(int j=0;j<=lst;j++) { 114 //debug<<"j = "<<j<<endl; 115 ret[i-j] = ( ret[i-j] - b[lst-j] * mul % mod + mod ) % mod; 116 //debug<<"ret[i-j] = "<<ret[i-j]<<endl; 117 } 118 } 119 //debug<<"at last ret = "; ret.print(); 120 return ret; 121 } 122 inline void print() const { 123 for(int i=0;i<lim<<2;i++) debug<<dat[i]<<" "; debug<<endl; 124 } 125 }pini,ptrans; 126 127 inline void NTT(lli* dst,int n,int ope) { 128 for(int i=0,j=0;i<n;i++) { 129 if( i < j ) swap( dst[i] , dst[j] ); 130 for(int t=n>>1;(j^=t)<t;t>>=1) ; 131 } 132 for(int len=2;len<=n;len<<=1) { 133 const int h = len >> 1; 134 lli per = fastpow(g,mod/(len)); 135 if( !~ope ) per = fastpow(per,mod-2); 136 for(int st=0;st<n;st+=len) { 137 lli w = 1; 138 for(int pos=0;pos<h;pos++) { 139 const lli u = dst[st+pos] , v = dst[st+pos+h] * w % mod; 140 dst[st+pos] = ( u + v ) % mod , 141 dst[st+pos+h] = ( u - v + mod ) % mod , 142 w = w * per % mod; 143 } 144 } 145 } 146 if( !~ope ) { 147 const lli mul = fastpow(n,mod-2); 148 for(int i=0;i<n;i++) dst[i] = dst[i] * mul % mod; 149 } 150 } 151 152 inline void initpoly() { 153 int len = lim << 2; 154 //trans.print(); 155 for(int i=0;i<len;i++) { 156 tmp = trans; 157 ptrans[i] = tmp.pointval(fastpow(g,(mod/len)*i)); 158 } 159 NTT(ptrans.dat,len,-1); 160 //ptrans.print(); 161 pini[1] = 1; 162 } 163 164 struct BigInt { 165 int dat[maxe],len; 166 inline void in(const char* s) { // s starts from 0 . 167 len = strlen(s); 168 for(int i=0;i<len;i++) dat[i] = s[len-i-1] - '0'; 169 } 170 inline bool andone() { 171 return dat[0] & 1; 172 } 173 inline void shr() { 174 for(int i=len-1;~i;i--) { 175 dat[i-1] += 10 * ( dat[i] & 1 ) , 176 dat[i] >>= 1; 177 } 178 while( len && !dat[len-1] ) --len; 179 } 180 inline bool iszero() { 181 return len == 0; 182 } 183 inline void minusone() { 184 --dat[0]; 185 for(int i=0;i<len;i++) 186 if( dat[i] < 0 ) dat[i] += 10 , dat[i+1]--; 187 while( len && !dat[len-1] ) --len; 188 } 189 }l,r; 190 191 bool vis[maxl],nxt[maxl]; 192 int s1,s2,m; 193 lli ans; 194 195 inline int zip() { 196 int ret = 0; 197 for(int i=0;i<6;i++) 198 ret += ( (int) nxt[i] << i ); 199 return ret; 200 } 201 inline void unzip(int sta) { 202 for(int i=0;i<m;i++) 203 vis[i] = ( sta >> i ) & 1; 204 } 205 inline void dfs(int pos,int sou,lli ways) { 206 if( pos == m ) { 207 ( mtrans.dat[sou][zip()] += ways ) %= mod; 208 return; 209 } 210 if( vis[pos] ) return dfs(pos+1,sou,ways); 211 else { 212 vis[pos] = nxt[pos] = 1; 213 dfs(pos+1,sou,ways*s1%mod); 214 vis[pos] = nxt[pos] = 0; 215 if( pos != m-1 && !vis[pos+1] ) { 216 vis[pos] = vis[pos+1] = 1; 217 dfs(pos+1,sou,ways*s2%mod); 218 vis[pos] = vis[pos+1] = 0; 219 } 220 } 221 } 222 223 inline Poly fastpow(Poly base,BigInt tim,Poly mod) { 224 Poly ret(1); 225 //debug<<"in fastpow inital ret = "; ret.print(); 226 while( !tim.iszero() ) { 227 if( tim.andone() ) ret = ret * base % mod; 228 tim.shr(); 229 if( !tim.iszero() ) base = base * base % mod; 230 } 231 return ret; 232 } 233 234 inline void merge(Matrix &dst,const Matrix &sou,int sx,int sy) { 235 for(int i=0;i<lim;i++) 236 for(int j=0;j<lim;j++) 237 dst.dat[i+sx][j+sy] = sou.dat[i][j]; 238 } 239 inline void init() { 240 lim = 1 << m; 241 for(int i=0;i<lim;i++) { 242 unzip(i); 243 dfs(0,i,1); 244 } 245 mini.dat[0][0] = 1; 246 merge(ini,mini,0,0) , merge(ini,mini,0,lim); 247 merge(trans,mtrans,0,0) , merge(trans,mtrans,0,lim) , merge(trans,Matrix(1),lim,lim); 248 } 249 250 inline lli calc(BigInt n) { 251 Matrix ret; 252 Poly mul = fastpow(pini,n,ptrans); 253 for(int i=0;i<lim<<1;i++) { 254 if( mul[i] ) ret = ( ret + pows[i] * mul[i] ); 255 } 256 return ret.dat[0][lim]; 257 } 258 inline void readin() { 259 static char buf[5002]; 260 scanf("%s",buf) , l.in(buf); 261 scanf("%s",buf) , r.in(buf); 262 l.minusone(); 263 } 264 265 int main() { 266 readin(); 267 scanf("%d%d%d",&m,&s1,&s2); 268 init(); 269 //debug<<"trans = "<<endl;trans.print(); 270 initpoly(); 271 pows[0] = ini; 272 for(int i=1;i<lim<<1;i++) pows[i] = pows[i-1] * trans; 273 ans = ( calc(r) - calc(l) + mod ) % mod; 274 printf("%lld ",ans); 275 return 0; 276 }
最终的85分代码:

1 #pragma GCC optimize(3) 2 #pragma GCC optimize("Ofast,no-stack-protector") 3 #pragma GCC optimize("-funsafe-loop-optimizations") 4 #pragma GCC optimize("-funroll-loops") 5 #pragma GCC optimize("-fwhole-program") 6 #include<cstdio> 7 #include<cstring> 8 #include<algorithm> 9 using namespace std; 10 typedef long long int lli; 11 const int maxn=70,maxl=10,maxe=2.6e3+1e2; 12 const int mod=998244353,g=3; 13 14 inline void duff_mul(lli* dst,const lli* sou,lli mul,unsigned len) { 15 unsigned loop = len >> 6; 16 switch( len & 63 ) { 17 case 0 : do { *dst++ += mul * *sou++ % mod; 18 case 63 : *dst++ += mul * *sou++ % mod; 19 case 62 : *dst++ += mul * *sou++ % mod; 20 case 61 : *dst++ += mul * *sou++ % mod; 21 case 60 : *dst++ += mul * *sou++ % mod; 22 case 59 : *dst++ += mul * *sou++ % mod; 23 case 58 : *dst++ += mul * *sou++ % mod; 24 case 57 : *dst++ += mul * *sou++ % mod; 25 case 56 : *dst++ += mul * *sou++ % mod; 26 case 55 : *dst++ += mul * *sou++ % mod; 27 case 54 : *dst++ += mul * *sou++ % mod; 28 case 53 : *dst++ += mul * *sou++ % mod; 29 case 52 : *dst++ += mul * *sou++ % mod; 30 case 51 : *dst++ += mul * *sou++ % mod; 31 case 50 : *dst++ += mul * *sou++ % mod; 32 case 49 : *dst++ += mul * *sou++ % mod; 33 case 48 : *dst++ += mul * *sou++ % mod; 34 case 47 : *dst++ += mul * *sou++ % mod; 35 case 46 : *dst++ += mul * *sou++ % mod; 36 case 45 : *dst++ += mul * *sou++ % mod; 37 case 44 : *dst++ += mul * *sou++ % mod; 38 case 43 : *dst++ += mul * *sou++ % mod; 39 case 42 : *dst++ += mul * *sou++ % mod; 40 case 41 : *dst++ += mul * *sou++ % mod; 41 case 40 : *dst++ += mul * *sou++ % mod; 42 case 39 : *dst++ += mul * *sou++ % mod; 43 case 38 : *dst++ += mul * *sou++ % mod; 44 case 37 : *dst++ += mul * *sou++ % mod; 45 case 36 : *dst++ += mul * *sou++ % mod; 46 case 35 : *dst++ += mul * *sou++ % mod; 47 case 34 : *dst++ += mul * *sou++ % mod; 48 case 33 : *dst++ += mul * *sou++ % mod; 49 case 32 : *dst++ += mul * *sou++ % mod; 50 case 31 : *dst++ += mul * *sou++ % mod; 51 case 30 : *dst++ += mul * *sou++ % mod; 52 case 29 : *dst++ += mul * *sou++ % mod; 53 case 28 : *dst++ += mul * *sou++ % mod; 54 case 27 : *dst++ += mul * *sou++ % mod; 55 case 26 : *dst++ += mul * *sou++ % mod; 56 case 25 : *dst++ += mul * *sou++ % mod; 57 case 24 : *dst++ += mul * *sou++ % mod; 58 case 23 : *dst++ += mul * *sou++ % mod; 59 case 22 : *dst++ += mul * *sou++ % mod; 60 case 21 : *dst++ += mul * *sou++ % mod; 61 case 20 : *dst++ += mul * *sou++ % mod; 62 case 19 : *dst++ += mul * *sou++ % mod; 63 case 18 : *dst++ += mul * *sou++ % mod; 64 case 17 : *dst++ += mul * *sou++ % mod; 65 case 16 : *dst++ += mul * *sou++ % mod; 66 case 15 : *dst++ += mul * *sou++ % mod; 67 case 14 : *dst++ += mul * *sou++ % mod; 68 case 13 : *dst++ += mul * *sou++ % mod; 69 case 12 : *dst++ += mul * *sou++ % mod; 70 case 11 : *dst++ += mul * *sou++ % mod; 71 case 10 : *dst++ += mul * *sou++ % mod; 72 case 9 : *dst++ += mul * *sou++ % mod; 73 case 8 : *dst++ += mul * *sou++ % mod; 74 case 7 : *dst++ += mul * *sou++ % mod; 75 case 6 : *dst++ += mul * *sou++ % mod; 76 case 5 : *dst++ += mul * *sou++ % mod; 77 case 4 : *dst++ += mul * *sou++ % mod; 78 case 3 : *dst++ += mul * *sou++ % mod; 79 case 2 : *dst++ += mul * *sou++ % mod; 80 case 1 : *dst++ += mul * *sou++ % mod; } while( loop-- ) ; 81 } 82 } 83 84 inline lli fastpow(lli base,int tim) { 85 lli ret = 1; 86 while( tim ) { 87 if( tim & 1 ) ret = ret * base % mod; 88 if( tim >>= 1 ) base = base * base % mod; 89 } 90 return ret; 91 } 92 int lim; 93 struct Matrix { 94 lli dat[maxn<<1][maxn<<1]; 95 Matrix(int tpe=0) { 96 memset(dat,0,sizeof(dat)); 97 if( tpe ) for(int i=0;i<lim;i++) dat[i][i] = 1; 98 } 99 friend Matrix operator * (const Matrix &a,const Matrix &b) { 100 Matrix ret; 101 /*for(int i=0;i<lim<<1;i++) 102 for(int j=0;j<lim<<1;j++) { 103 for(int k=0;k<lim<<1;k++) 104 //( ret.dat[i][j] += a.dat[i][k] * b.dat[k][j] % mod ) %= mod; 105 ret.dat[i][j] += a.dat[i][k] * b.dat[k][j] % mod; 106 ret.dat[i][j] %= mod; 107 }*/ 108 for(int i=0;i<lim<<1;i++) { 109 for(int k=0;k<lim<<1;k++) { 110 const lli t = a.dat[i][k]; 111 if( t ) { 112 /*for(int j=0;j<lim<<1;j++) 113 ret.dat[i][j] += t * b.dat[k][j] % mod;*/ 114 duff_mul(ret.dat[i],b.dat[k],t,lim<<1); 115 } 116 } 117 } 118 for(int i=0;i<lim<<1;i++) 119 for(int j=0;j<lim<<1;j++) 120 ret.dat[i][j] %= mod; 121 return ret; 122 } 123 friend Matrix operator + (const Matrix &a,const Matrix &b) { 124 Matrix ret; 125 for(int i=0;i<lim<<1;i++) 126 for(int j=0;j<lim<<1;j++) 127 ret.dat[i][j] = ( a.dat[i][j] + b.dat[i][j] ) % mod; 128 return ret; 129 } 130 friend Matrix operator * (const Matrix &a,const lli &b) { 131 Matrix ret; 132 for(int i=0;i<lim<<1;i++) 133 for(int j=0;j<lim<<1;j++) 134 ret.dat[i][j] = a.dat[i][j] * b % mod; 135 return ret; 136 } 137 inline lli pointval(const lli &x) { 138 const int len = lim << 1; 139 lli ret = 1; 140 for(int i=0;i<len;i++) dat[i][i] = ( dat[i][i] - x % mod + mod ) % mod; 141 for(int i=0;i<len;i++) { 142 int pos = -1; 143 for(int j=i;j<len;j++) if( dat[j][i] ) { 144 pos = j; 145 break; 146 } 147 if( !~pos ) return 0; 148 if( pos != i ) { 149 ret = mod - ret; 150 for(int k=0;k<len;k++) swap( dat[i][k] , dat[pos][k] ); 151 pos = i; 152 } 153 const lli mul = fastpow(dat[i][i],mod-2); 154 ret = ret * dat[i][i] % mod; 155 for(int k=0;k<len;k++) dat[i][k] = dat[i][k] * mul % mod; 156 for(int j=0;j<len;j++) if( dat[j][i] && j != i ) { 157 const lli mul = dat[j][i]; 158 for(int k=0;k<len;k++) dat[j][k] = ( dat[j][k] - dat[i][k] * mul % mod + mod ) % mod; 159 } 160 } 161 return ret; 162 } 163 }mtrans,mini,trans,ini,tmp,pows[maxn<<1]; 164 165 lli invblst; 166 167 struct Poly { 168 lli dat[maxn<<2]; 169 Poly(int tpe = 0) { 170 memset(dat,0,sizeof(dat)); 171 *dat = tpe; 172 } 173 lli& operator [] (const int &x) { 174 return dat[x]; 175 } 176 const lli& operator [] (const int &x) const { 177 return dat[x]; 178 } 179 friend Poly operator * (const Poly &a,const Poly &b) { 180 Poly ret; 181 for(int i=0;i<lim<<1;i++) 182 for(int j=0;j<lim<<1;j++) 183 //( ret[i+j] += a[i] * b[j] % mod ) %= mod; 184 ret[i+j] += a[i] * b[j] % mod; 185 for(int i=0;i<lim<<1;i++) ret[i] %= mod; 186 return ret; 187 } 188 friend Poly operator % (const Poly &a,const Poly &b) { 189 Poly ret = a; 190 int lst = lim << 1; 191 while( lst && !b[lst] ) --lst; 192 for(int i=(lim<<2)-1;i>=lst;i--) if( ret[i] ) { 193 const int mul = ret[i] * invblst; 194 for(int j=0;j<=lst;j++) { 195 ret[i-j] = ( ret[i-j] - b[lst-j] * mul % mod + mod ) % mod; 196 } 197 } 198 return ret; 199 } 200 }pini,ptrans; 201 202 inline void NTT(lli* dst,int n,int ope) { 203 for(int i=0,j=0;i<n;i++) { 204 if( i < j ) swap( dst[i] , dst[j] ); 205 for(int t=n>>1;(j^=t)<t;t>>=1) ; 206 } 207 for(int len=2;len<=n;len<<=1) { 208 const int h = len >> 1; 209 lli per = fastpow(g,mod/(len)); 210 if( !~ope ) per = fastpow(per,mod-2); 211 for(int st=0;st<n;st+=len) { 212 lli w = 1; 213 for(int pos=0;pos<h;pos++) { 214 const lli u = dst[st+pos] , v = dst[st+pos+h] * w % mod; 215 dst[st+pos] = ( u + v ) % mod , 216 dst[st+pos+h] = ( u - v + mod ) % mod , 217 w = w * per % mod; 218 } 219 } 220 } 221 if( !~ope ) { 222 const lli mul = fastpow(n,mod-2); 223 for(int i=0;i<n;i++) dst[i] = dst[i] * mul % mod; 224 } 225 } 226 227 inline void initpoly() { 228 int len = lim << 2; 229 for(int i=0;i<len;i++) { 230 tmp = trans; 231 ptrans[i] = tmp.pointval(fastpow(g,(mod/len)*i)); 232 } 233 NTT(ptrans.dat,len,-1); 234 pini[1] = 1; 235 int lst = len; 236 while( !ptrans.dat[lst] ) --lst; 237 invblst = fastpow(ptrans.dat[lst],mod-2); 238 } 239 240 struct BigInt { 241 int dat[maxe],len; 242 inline void in(const char* s) { // s starts from 0 . 243 len = strlen(s); 244 for(int i=0;i<len;i++) dat[i] = s[len-i-1] - '0'; 245 } 246 inline bool andone() { 247 return dat[0] & 1; 248 } 249 inline void shr() { 250 for(int i=len-1;~i;i--) { 251 dat[i-1] += 10 * ( dat[i] & 1 ) , 252 dat[i] >>= 1; 253 } 254 while( len && !dat[len-1] ) --len; 255 } 256 inline bool iszero() { 257 return len == 0; 258 } 259 inline void minusone() { 260 --dat[0]; 261 for(int i=0;i<len;i++) 262 if( dat[i] < 0 ) dat[i] += 10 , dat[i+1]--; 263 while( len && !dat[len-1] ) --len; 264 } 265 }l,r; 266 267 bool vis[maxl],nxt[maxl]; 268 int s1,s2,m; 269 lli ans; 270 271 inline int zip() { 272 int ret = 0; 273 for(int i=0;i<6;i++) 274 ret += ( (int) nxt[i] << i ); 275 return ret; 276 } 277 inline void unzip(int sta) { 278 for(int i=0;i<m;i++) 279 vis[i] = ( sta >> i ) & 1; 280 } 281 inline void dfs(int pos,int sou,lli ways) { 282 if( pos == m ) { 283 ( mtrans.dat[sou][zip()] += ways ) %= mod; 284 return; 285 } 286 if( vis[pos] ) return dfs(pos+1,sou,ways); 287 else { 288 vis[pos] = nxt[pos] = 1; 289 dfs(pos+1,sou,ways*s1%mod); 290 vis[pos] = nxt[pos] = 0; 291 if( pos != m-1 && !vis[pos+1] ) { 292 vis[pos] = vis[pos+1] = 1; 293 dfs(pos+1,sou,ways*s2%mod); 294 vis[pos] = vis[pos+1] = 0; 295 } 296 } 297 } 298 299 inline Poly fastpow(Poly base,BigInt tim,Poly mod) { 300 Poly ret(1); 301 while( !tim.iszero() ) { 302 if( tim.andone() ) ret = ret * base % mod; 303 tim.shr(); 304 if( !tim.iszero() ) base = base * base % mod; 305 } 306 return ret; 307 } 308 309 inline void merge(Matrix &dst,const Matrix &sou,int sx,int sy) { 310 for(int i=0;i<lim;i++) 311 for(int j=0;j<lim;j++) 312 dst.dat[i+sx][j+sy] = sou.dat[i][j]; 313 } 314 inline void init() { 315 lim = 1 << m; 316 for(int i=0;i<lim;i++) { 317 unzip(i); 318 dfs(0,i,1); 319 } 320 mini.dat[0][0] = 1; 321 merge(ini,mini,0,0) , merge(ini,mini,0,lim); 322 merge(trans,mtrans,0,0) , merge(trans,mtrans,0,lim) , merge(trans,Matrix(1),lim,lim); 323 } 324 325 inline lli calc(BigInt n) { 326 Matrix ret; 327 Poly mul = fastpow(pini,n,ptrans); 328 for(int i=0;i<lim<<1;i++) { 329 if( mul[i] ) ret = ( ret + pows[i] * mul[i] ); 330 } 331 return ret.dat[0][lim]; 332 } 333 inline void readin() { 334 static char buf[5002]; 335 scanf("%s",buf) , l.in(buf); 336 scanf("%s",buf) , r.in(buf); 337 l.minusone(); 338 } 339 340 int main() { 341 readin(); 342 scanf("%d%d%d",&m,&s1,&s2); 343 init(); 344 initpoly(); 345 pows[0] = ini; 346 for(int i=1;i<lim<<1;i++) pows[i] = pows[i-1] * trans; 347 ans = ( calc(r) - calc(l) + mod ) % mod; 348 printf("%lld ",ans); 349 return 0; 350 }
T3:


显然最优的点一定在这条链上,且答案显然单峰。
我们可以三分这个点,然后用树链剖分线段树计算答案。
线段树维护一下dis[i]*in[i],(inf-dis[i])*in[i],然后计算的时候花式讨论就好了。
然而考场上没时间写,打了20分暴力......
后来发现这样3个log的算法并不能AC,只有65分......
三分改成求导后二分,大力卡常获得90分......
还是自己太菜,弃疗了......
以下是官方题解:

考场20分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<cstdlib> 6 #define debug cout 7 typedef long long int lli; 8 using namespace std; 9 const int maxn=2.5e3+1e2; 10 const lli inf=0x3f3f3f3f3f3f3f3fll; 11 12 int s[maxn],t[maxn<<1],nxt[maxn<<1],l[maxn<<1]; 13 int lcas[maxn][maxn]; 14 int siz[maxn],top[maxn],fa[maxn],son[maxn],dep[maxn],dd[maxn]; 15 int seq[maxn],len; 16 lli in[maxn]; 17 18 inline void addedge(int from,int to,int len) { 19 static int cnt = 0; 20 t[++cnt] = to , l[cnt] = len , 21 nxt[cnt] = s[from] , s[from] = cnt; 22 } 23 inline void pre(int pos) { 24 siz[pos] = 1; 25 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) { 26 dep[t[at]] = dep[pos] + 1 , dd[t[at]] = dd[pos] + l[at] , fa[t[at]] = pos , 27 pre(t[at]) , siz[pos] += siz[t[at]]; 28 if( siz[t[at]] > siz[son[pos]] ) son[pos] = t[at]; 29 } 30 } 31 inline void dfs(int pos) { 32 top[pos] = pos == son[fa[pos]] ? top[fa[pos]] : pos; 33 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) dfs(t[at]); 34 } 35 inline int lca(int x,int y) { 36 while( top[x] != top[y] ) { 37 if( dep[top[x]] < dep[top[y]] ) swap(x,y); 38 x = fa[top[x]]; 39 } 40 return dep[x] < dep[y] ? x : y; 41 } 42 43 inline void chain(int pos,int tar) { 44 while( pos != tar ) seq[++len] = pos , pos = fa[pos]; 45 } 46 inline void getchain(int x,int y) { 47 int l = lcas[x][y]; len = 0; 48 chain(x,l) , seq[++len] = l; 49 const int lastlen = len; 50 chain(y,l); 51 if( len != lastlen ) reverse(seq+lastlen+1,seq+len+1); 52 } 53 inline int dis(int x,int y) { 54 return dd[x] + dd[y] - ( dd[lcas[x][y]] << 1 ); 55 } 56 inline lli calc(int pos) { 57 lli ret = 0; 58 for(int i=1;i<=len;i++) ret += in[seq[i]] * dis(pos,seq[i]); 59 return ret; 60 } 61 inline lli tri() { 62 int ll = 1 , rr = len , lmid , rmid; 63 lli ret = inf; 64 while( rr > ll + 2 ) { 65 lmid = ( ll + ll + rr ) / 3 , rmid = ( ll + rr + rr ) / 3; 66 if( calc(seq[lmid]) < calc(seq[rmid]) ) rr = rmid; 67 else ll = lmid; 68 } 69 for(int i=ll;i<=rr;i++) { 70 ret = min( ret , calc(seq[i]) ); 71 } 72 return ret; 73 } 74 75 int main() { 76 static int n,m; 77 scanf("%d",&n); 78 for(int i=1;i<=n;i++) scanf("%lld",in+i); 79 for(int i=1,a,b,l;i<n;i++) { 80 scanf("%d%d%d",&a,&b,&l) , 81 addedge(a,b,l) , addedge(b,a,l); 82 } 83 pre(1) , dfs(1); 84 for(int i=1;i<=n;i++) for(int j=1;j<=i;j++) lcas[i][j] = lcas[j][i] = lca(i,j); 85 scanf("%d",&m); 86 for(int i=1,o,x,y;i<=m;i++) { 87 scanf("%d%d%d",&o,&x,&y); 88 if( o == 1 ) { 89 getchain(x,y); 90 printf("%lld ",tri()); 91 } else in[x] = y; 92 } 93 return 0; 94 }
65分三分代码:

1 #pragma GCC optimize(3) 2 #pragma GCC optimize("Ofast,no-stack-protector") 3 #pragma GCC optimize("-funsafe-loop-optimizations") 4 #pragma GCC optimize("-funroll-loops") 5 #pragma GCC optimize("-fwhole-program") 6 #include<cstdio> 7 #include<algorithm> 8 #include<cctype> 9 typedef long long int lli; 10 const int maxn=153000; 11 const lli inf=0x3f3f3f3f3f3f3f3fll; 12 13 int s[maxn],t[maxn<<1],nxt[maxn<<1],in[maxn]; 14 lli dis[maxn],rdis[maxn]; // rdis root = 1e11 . 15 int fa[maxn],siz[maxn],dep[maxn],top[maxn],son[maxn],id[maxn],cov[maxn]; 16 int l[maxn<<2],r[maxn<<2],lson[maxn<<2],rson[maxn<<2],prec[maxn<<2],cnt; 17 int rec[maxn]; 18 19 struct Node { 20 lli s,vs,rvs; 21 inline void in(const int &x) { 22 s = ::in[x] , vs = dis[x] * ::in[x] , rvs = rdis[x] * ::in[x]; 23 } 24 friend Node operator + (const Node &a,const Node &b) { 25 return (Node){a.s+b.s,a.vs+b.vs,a.rvs+b.rvs}; 26 } 27 friend Node operator += (Node &a,const Node &b) { 28 return a = a + b; 29 } 30 }ns[maxn<<2]; 31 32 inline void build(int pos,const int &ll,const int &rr) { 33 l[pos] = ll , r[pos] = rr; 34 if( ll == rr ) return ns[pos].in(prec[pos]=rec[ll]); 35 const int mid = ( ll + rr ) >> 1; 36 build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr); 37 ns[pos] = ns[lson[pos]] + ns[rson[pos]]; 38 } 39 inline void update(int pos,const int &tar) { 40 if( l[pos] == r[pos] ) return ns[pos].in(prec[pos]); 41 const int mid = ( l[pos] + r[pos] ) >> 1; 42 if( tar <= mid ) update(lson[pos],tar); 43 else update(rson[pos],tar); 44 ns[pos] = ns[lson[pos]] + ns[rson[pos]]; 45 } 46 inline Node query(int pos,const int &ll,const int &rr) { 47 if( ll <= l[pos] && r[pos] <= rr ) return ns[pos]; 48 const int mid = ( l[pos] + r[pos] ) >> 1; 49 if( rr <= mid ) return query(lson[pos],ll,rr); 50 else if( ll > mid ) return query(rson[pos],ll,rr); 51 return query(lson[pos],ll,rr) + query(rson[pos],ll,rr); 52 } 53 inline int kth(int pos,const int &ll,const int &rr,int k) { // k from top to bottom . 54 if( l[pos] == r[pos] ) return prec[pos]; 55 const int mid = ( l[pos] + r[pos] ) >> 1; 56 if( rr <= mid ) return kth(lson[pos],ll,rr,k); 57 else if( ll > mid ) return kth(rson[pos],ll,rr,k); 58 if( k > mid - std::max(ll,l[pos]) + 1 ) return kth(rson[pos],ll,rr,k-(mid-std::max(ll,l[pos])+1)); 59 else return kth(lson[pos],ll,rr,k); 60 } 61 inline int chain_kth(int x,const int &l,int k) { // k from bottom to top . 62 while( top[x] != top[l] ) { 63 if( k <= dep[x] - dep[top[x]] + 1 ) { 64 return kth(cov[top[x]],id[top[x]],id[x],(dep[x]-dep[top[x]]+1)-k+1); 65 } 66 else k -= dep[x]-dep[top[x]]+1 , x = fa[top[x]]; 67 } 68 return kth(cov[top[l]],id[l],id[x],(dep[x]-dep[l]+1)-k+1); 69 } 70 inline Node chain(int x,const int &tp) { // includeing top . 71 Node ret = (Node){0,0,0}; 72 while( top[x] != top[tp] ) { 73 ret += query(cov[top[x]],id[top[x]],id[x]) , x = fa[top[x]]; 74 } 75 ret += query(cov[top[x]],id[tp],id[x]); 76 return ret; 77 } 78 inline int lca(int x,int y) { 79 while( top[x] != top[y] ) 80 if( dep[top[x]] > dep[top[y]] ) x = fa[top[x]]; 81 else y = fa[top[y]]; 82 return dep[x] < dep[y] ? x : y; 83 } 84 85 inline lli query_corner(const int &p,const int &x,const int &y,const int &l) { // pos at side of x . 86 lli ret = 0; 87 Node chainy = chain(y,l) , chainx = chain(x,p) , chainp = chain(p,l); 88 ret += chainy.vs - chainy.s * dis[l]; 89 ret += chainx.vs - chainx.s * dis[p]; 90 ret += chainp.rvs - chainp.s * rdis[p]; 91 ret += ( chainy.s - in[l] ) * ( dis[p] - dis[l] ); 92 return ret; 93 } 94 inline lli query_chain(const int &p,const int &x,const int &y) { // y is the lca . 95 lli ret = 0; 96 Node chainx = chain(x,p) , chainp = chain(p,y); 97 ret += chainx.vs - chainx.s * dis[p]; 98 ret += chainp.rvs - chainp.s * rdis[p]; 99 return ret; 100 } 101 inline lli getans(int x,int y) { 102 if( x == y ) return 0; 103 int l = lca(x,y); 104 lli ret = inf; 105 if( l == x || l == y ) { 106 if( l != y ) std::swap(x,y); 107 int ll = 1 , rr = dep[x] - dep[y] + 1 , lmid , rmid , lp , rp , p; 108 while( rr > ll + 2 ) { 109 lmid = ( ll + ll + rr ) / 3 , rmid = ( ll + rr + rr ) / 3; 110 lp = chain_kth(x,y,lmid) , rp = chain_kth(x,y,rmid); 111 if( query_chain(lp,x,y) < query_chain(rp,x,y) ) rr = rmid; 112 else ll = lmid; 113 } 114 for(int i=ll;i<=rr;i++) { 115 p = chain_kth(x,y,i); 116 ret = std::min( ret , query_chain(p,x,y) ); 117 } 118 } else { 119 lli sumx = chain(x,l).s , sumy = chain(y,l).s; 120 if( sumx == sumy ) { 121 Node chainx = chain(x,l) , chainy = chain(y,l); 122 return chainx.vs + chainy.vs - dis[l] * (chainx.s+chainy.s); 123 } 124 if( sumx < sumy ) std::swap(x,y); 125 int ll = 1 , rr = dep[x] - dep[l] + 1 , lmid , rmid , lp , rp , p; 126 while( rr > ll + 2 ) { 127 lmid = ( ll + ll + rr ) / 3 , rmid = ( ll + rr + rr ) / 3; 128 lp = chain_kth(x,l,lmid) , rp = chain_kth(x,l,rmid); 129 if( query_corner(lp,x,y,l) < query_corner(rp,x,y,l) ) rr = rmid; 130 else ll = lmid; 131 } 132 for(int i=ll;i<=rr;i++) { 133 p = chain_kth(x,l,i); 134 ret = std::min( ret , query_corner(p,x,y,l) ); 135 } 136 } 137 return ret; 138 } 139 140 inline void addedge(const int &from,const int &to,const int &len) { 141 static int cnt = 0; 142 t[++cnt] = to , l[cnt] = len , 143 nxt[cnt] = s[from] , s[from] = cnt; 144 } 145 inline void pre(int pos) { 146 siz[pos] = 1; 147 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) { 148 fa[t[at]] = pos , dep[t[at]] = dep[pos] + 1 , 149 dis[t[at]] = dis[pos] + l[at] , rdis[t[at]] = rdis[pos] - l[at]; 150 pre(t[at]) , siz[pos] += siz[t[at]]; 151 if( siz[t[at]] > siz[son[pos]] ) son[pos] = t[at]; 152 } 153 } 154 inline void dfs(int pos) { 155 top[pos] = pos == son[fa[pos]] ? top[fa[pos]] : pos; 156 id[pos] = pos == son[fa[pos]] ? id[fa[pos]] + 1 : 1; 157 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) dfs(t[at]); 158 if( !son[pos] ) { 159 for(int i=pos;;i=fa[i]) { 160 rec[id[i]] = i; 161 if( i == top[pos] ) break; 162 } 163 build(cov[top[pos]]=++cnt,id[top[pos]],id[pos]); 164 } 165 } 166 167 const int BS = 1 << 23; 168 char buf[BS],*st=buf+BS,*ed=buf+BS; 169 inline char nextchar() { 170 return *st++; 171 } 172 173 inline int getint() { 174 int ret = 0 , ch; 175 while( !isdigit(ch=nextchar()) ); 176 do ret=ret*10+ch-'0'; while( isdigit(ch=nextchar()) ); 177 return ret; 178 } 179 180 int main() { 181 ed = buf + fread(st=buf,1,BS,stdin); 182 static int n,m; 183 n = getint(); 184 for(int i=1;i<=n;i++) in[i] = getint(); 185 for(int i=1,a,b,l;i<n;i++) { 186 a = getint() , b = getint() , l = getint(); 187 addedge(a,b,l) , addedge(b,a,l); 188 } 189 rdis[1] = 1e11; 190 pre(1) , dfs(1); 191 m = getint(); 192 for(int i=1,o,x,y;i<=m;i++) { 193 o = getint() , x = getint() , y = getint(); 194 if( o == 1 ) printf("%lld ",getans(x,y)); 195 else if( o == 2 ) { 196 in[x] = y; 197 update(cov[top[x]],id[x]); 198 } 199 } 200 return 0; 201 }
90分二分代码:

1 #pragma GCC optimize(3) 2 #pragma GCC optimize("Ofast,no-stack-protector") 3 #pragma GCC optimize("-funsafe-loop-optimizations") 4 #pragma GCC optimize("-funroll-loops") 5 #pragma GCC optimize("-fwhole-program") 6 #include<cstdio> 7 #include<algorithm> 8 #include<cctype> 9 typedef long long int lli; 10 const int maxn=153000; 11 const lli inf=0x3f3f3f3f3f3f3f3fll; 12 13 int s[maxn],t[maxn<<1],nxt[maxn<<1],l[maxn<<1],in[maxn]; 14 lli dis[maxn],rdis[maxn]; // rdis root = 1e11 . 15 int fa[maxn],siz[maxn],dep[maxn],top[maxn],son[maxn],id[maxn],cov[maxn],delta[maxn]; 16 int lson[maxn<<2],rson[maxn<<2],prec[maxn<<2],cnt; 17 int rec[maxn]; 18 19 struct Node { 20 lli s,vs,rvs; 21 inline void in(const int &x) { 22 s = ::in[x] , vs = dis[x] * ::in[x] , rvs = rdis[x] * ::in[x]; 23 } 24 friend Node operator + (const Node &a,const Node &b) { 25 return (Node){a.s+b.s,a.vs+b.vs,a.rvs+b.rvs}; 26 } 27 friend Node operator += (Node &a,const Node &b) { 28 return a = a + b; 29 } 30 }ns[maxn<<2]; 31 32 inline void build(int pos,const int &ll,const int &rr) { 33 if( ll == rr ) return ns[pos].in(prec[pos]=rec[ll]); 34 const int mid = ( ll + rr ) >> 1; 35 build(lson[pos]=++cnt,ll,mid) , build(rson[pos]=++cnt,mid+1,rr); 36 ns[pos] = ns[lson[pos]] + ns[rson[pos]]; 37 } 38 inline void update(int pos,const int &l,const int &r,const int &tar) { 39 if( l == r ) return ns[pos].in(prec[pos]); 40 const int mid = ( l + r ) >> 1; 41 if( tar <= mid ) update(lson[pos],l,mid,tar); 42 else update(rson[pos],mid+1,r,tar); 43 ns[pos] = ns[lson[pos]] + ns[rson[pos]]; 44 } 45 inline Node query(int pos,const int &l,const int &r,const int &ll,const int &rr) { 46 if( ll <= l && r <= rr ) return ns[pos]; 47 const int mid = ( l + r ) >> 1; 48 if( rr <= mid ) return query(lson[pos],l,mid,ll,rr); 49 else if( ll > mid ) return query(rson[pos],mid+1,r,ll,rr); 50 return query(lson[pos],l,mid,ll,rr) + query(rson[pos],mid+1,r,ll,rr); 51 } 52 inline lli query_sum(int pos,const int &l,const int &r,const int &ll,const int &rr) { 53 if( ll <= l && r <= rr ) return ns[pos].s; 54 const int mid = ( l + r ) >> 1; 55 if( rr <= mid ) return query_sum(lson[pos],l,mid,ll,rr); 56 else if( ll > mid ) return query_sum(rson[pos],mid+1,r,ll,rr); 57 return query_sum(lson[pos],l,mid,ll,rr) + query_sum(rson[pos],mid+1,r,ll,rr); 58 } 59 inline int kth(int pos,const int &l,const int &r,const int &ll,const int &rr,int k) { // k from top to bottom . 60 if( l == r ) return prec[pos]; 61 const int mid = ( l + r ) >> 1; 62 if( rr <= mid ) return kth(lson[pos],l,mid,ll,rr,k); 63 else if( ll > mid ) return kth(rson[pos],mid+1,r,ll,rr,k); 64 if( k > mid - std::max(ll,l) + 1 ) return kth(rson[pos],mid+1,r,ll,rr,k-(mid-std::max(ll,l)+1)); 65 else return kth(lson[pos],l,mid,ll,rr,k); 66 } 67 inline int chain_kth(int x,const int &l,int k) { // k from bottom to top . 68 while( top[x] != top[l] ) { 69 if( k <= dep[x] - dep[top[x]] + 1 ) return kth(cov[top[x]],1,delta[top[x]],id[top[x]],id[x],(dep[x]-dep[top[x]]+1)-k+1); 70 else k -= dep[x]-dep[top[x]]+1 , x = fa[top[x]]; 71 } 72 return kth(cov[top[l]],1,delta[top[x]],id[l],id[x],(dep[x]-dep[l]+1)-k+1); 73 } 74 inline Node chain(int x,const int &tp) { // includeing top . 75 Node ret = (Node){0,0,0}; 76 while( top[x] != top[tp] ) { 77 ret += query(cov[top[x]],1,delta[top[x]],id[top[x]],id[x]) , x = fa[top[x]]; 78 } 79 ret += query(cov[top[x]],1,delta[top[x]],id[tp],id[x]); 80 return ret; 81 } 82 inline lli chain_sum(int x,const int &tp) { // includeing top . 83 lli ret = 0; 84 while( top[x] != top[tp] ) { 85 ret += query_sum(cov[top[x]],1,delta[top[x]],id[top[x]],id[x]) , x = fa[top[x]]; 86 } 87 ret += query_sum(cov[top[x]],1,delta[top[x]],id[tp],id[x]); 88 return ret; 89 } 90 inline int lca(int x,int y) { 91 while( top[x] != top[y] ) 92 if( dep[top[x]] > dep[top[y]] ) x = fa[top[x]]; 93 else y = fa[top[y]]; 94 return dep[x] < dep[y] ? x : y; 95 } 96 97 inline lli query_corner(const int &p,const int &x,const int &y,const int &l) { // pos at side of x . 98 lli ret = 0; 99 Node chainy = chain(y,l) , chainx = chain(x,p) , chainp = chain(p,l); 100 ret += chainy.vs - chainy.s * dis[l]; 101 ret += chainx.vs - chainx.s * dis[p]; 102 ret += chainp.rvs - chainp.s * rdis[p]; 103 ret += ( chainy.s - in[l] ) * ( dis[p] - dis[l] ); 104 return ret; 105 } 106 inline lli query_chain(const int &p,const int &x,const int &y) { // y is the lca . 107 lli ret = 0; 108 Node chainx = chain(x,p) , chainp = chain(p,y); 109 ret += chainx.vs - chainx.s * dis[p]; 110 ret += chainp.rvs - chainp.s * rdis[p]; 111 return ret; 112 } 113 inline lli getans(int x,int y) { 114 if( x == y ) return 0; 115 int l = lca(x,y); 116 lli ret = inf; 117 if( l == x || l == y ) { 118 if( l != y ) std::swap(x,y); // Now lca = y . 119 int ll = 1 , rr = dep[x] - dep[y] + 1 , mid , mip; 120 while( rr > ll + 1 ) { 121 mid = ( ll + rr ) >> 1 , mip = chain_kth(x,y,mid); 122 const lli suml = chain_sum(mip,y) , sumr = chain_sum(x,mip); 123 if( suml < sumr ) rr = mid; 124 else ll = mid; 125 } 126 for(int i=ll,p;i<=rr;++i) { 127 p = chain_kth(x,y,i); 128 ret = std::min( ret , query_chain(p,x,y) ); 129 } 130 } else { 131 lli sumx = chain_sum(x,l) , sumy = chain_sum(y,l); 132 if( sumx == sumy ) { 133 Node chainx = chain(x,l) , chainy = chain(y,l); 134 return chainx.vs + chainy.vs - dis[l] * (chainx.s+chainy.s); 135 } 136 if( sumx < sumy ) std::swap(x,y) , std::swap(sumx,sumy); 137 sumy -= in[l]; 138 int ll = 1 , rr = dep[x] - dep[l] + 1 , mid , mip; 139 while( rr > ll + 1 ) { 140 mid = ( ll + rr ) >> 1 , mip = chain_kth(x,l,mid); 141 const lli suml = chain_sum(mip,l) + sumy , sumr = chain_sum(x,mip); 142 if( suml < sumr ) rr = mid; 143 else ll = mid; 144 } 145 for(int i=ll,p;i<=rr;++i) { 146 p = chain_kth(x,l,i); 147 ret = std::min( ret , query_corner(p,x,y,l) ); 148 } 149 } 150 return ret; 151 } 152 153 inline void addedge(const int &from,const int &to,const int &len) { 154 static int cnt = 0; 155 t[++cnt] = to , l[cnt] = len , 156 nxt[cnt] = s[from] , s[from] = cnt; 157 } 158 inline void pre(int pos) { 159 siz[pos] = 1; 160 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) { 161 fa[t[at]] = pos , dep[t[at]] = dep[pos] + 1 , 162 dis[t[at]] = dis[pos] + l[at] , rdis[t[at]] = rdis[pos] - l[at]; 163 pre(t[at]) , siz[pos] += siz[t[at]]; 164 if( siz[t[at]] > siz[son[pos]] ) son[pos] = t[at]; 165 } 166 } 167 inline void dfs(int pos) { 168 top[pos] = pos == son[fa[pos]] ? top[fa[pos]] : pos; 169 id[pos] = pos == son[fa[pos]] ? id[fa[pos]] + 1 : 1; 170 for(int at=s[pos];at;at=nxt[at]) if( t[at] != fa[pos] ) dfs(t[at]); 171 if( !son[pos] ) { 172 for(int i=pos;;i=fa[i]) { 173 rec[id[i]] = i; 174 if( i == top[pos] ) break; 175 } 176 delta[top[pos]] = id[pos]; 177 build(cov[top[pos]]=++cnt,id[top[pos]],id[pos]); 178 } 179 } 180 181 const int BS = 1 << 23; 182 char buf[BS],*st=buf+BS,*ed=buf+BS; 183 inline char nextchar() { 184 return *st++; 185 } 186 inline void printchar(char x) { 187 static char buf[1<<22],*st=buf,*ed=buf+(1<<22); 188 if( x == -1 ) { 189 fwrite(buf,1,st-buf,stdout); 190 st = buf; 191 return; 192 } 193 if( st == ed ) fwrite(st=buf,1,1<<22,stdout); 194 *st++ = x; 195 } 196 inline void printint(lli x) { 197 static int stk[35],top; 198 if( !x ) { 199 printchar('0'); 200 } else { 201 while( x ) stk[++top] = x % 10 , x /= 10; 202 while( top ) printchar('0'+stk[top--]); 203 } 204 printchar(' '); 205 } 206 207 inline int getint() { 208 int ret = 0 , ch; 209 while( !isdigit(ch=nextchar()) ); 210 do ret=ret*10+ch-'0'; while( isdigit(ch=nextchar()) ); 211 return ret; 212 } 213 214 int main() { 215 ed = buf + fread(st=buf,1,BS,stdin); 216 static int n,m; 217 n = getint(); 218 for(int i=1;i<=n;++i) in[i] = getint(); 219 for(int i=1,a,b,l;i<n;++i) { 220 a = getint() , b = getint() , l = getint(); 221 addedge(a,b,l) , addedge(b,a,l); 222 } 223 rdis[1] = 1e11; 224 pre(1) , dfs(1); 225 m = getint(); 226 for(int i=1,o,x,y;i<=m;++i) { 227 o = getint() , x = getint() , y = getint(); 228 if( o == 1 ) printint(getans(x,y)); 229 else if( o == 2 ) { 230 in[x] = y; 231 update(cov[top[x]],1,delta[top[x]],id[x]); 232 } 233 } 234 printchar(-1); 235 return 0; 236 }
最后上神TM卡常的图片......