今天又有一场愉悦的考试。
早晨就知道下午两点考试,直觉告诉我考反演。于是便十分不安,开始补习组合数学。结果困得要命,趴在桌上睡得天昏地暗……做梦梦见自己翻在地上两次……
中午闹钟没响,然后就很愉悦地起晚了,赶紧到学校卡着点坐在了电脑前面。
然后就有了下面的故事:
T1:
链接:EZOJ_Alpha:P1079

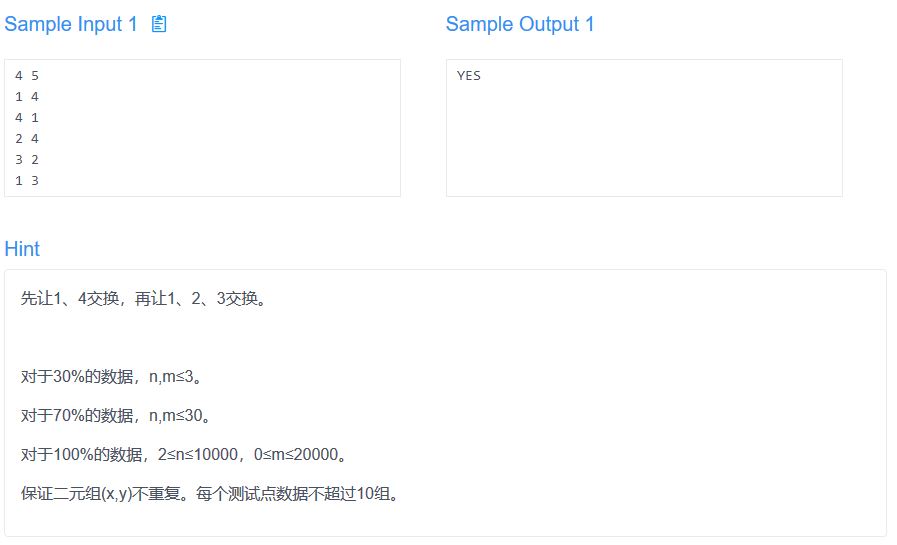
那个交换方式炸胡!只要存在完美匹配一定能构造出方案,且不存在完美匹配一定无解(后半句显然,前半句的意思是如果有完美匹配的话你可以构造一个或多个环去交换。自行脑补就可以了)。
什么你告诉我你不会证明?好好好,有请我们的归纳法君。
首先我们先证明:如果总共有i个点,那么我们从中任取i-1个点一定多个环和至多一条链:
如果存在两条链的话,只有一条头应该连i,只有一条的尾被i连,那么剩下的两个接头无法无法在这i个点中连接,与只有i个点矛盾。假设不成立,原命题得证。
首先只有一个点的情况能构造出方案。
然后考虑前面有i个点构成多个闭环,我们要放入第i个点。
如果第i个点能直接插入某个环中(即i连接断点前驱,断点后继连接i),那么方案构造完成。
否则,让i连接其完美匹配中的前驱,让i在完美匹配中的后继连接i,那么剩下两个断点。因为存在完美匹配,所以一定能够通过调整其他点的一些关系使这两个断点相连,方案构造完成。
其实不需要归纳法,考虑图论的话,i个点i条边,每个点一出度一入度一定是多个环QAQ。
然后直接dinic最大匹配。
考场上我不知道这东西的复杂度,几分钟想出了正解不敢写,写了怕不能AC,写了一个maker进行对拍,发现10组数据平均递归1e7次左右就能完成。然而我机器太慢还是比2s多。弃坑走人。
代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #include<cctype> 7 #define debug cout 8 using namespace std; 9 const int maxn=1e4+1e2,maxm=2e4+1e2; 10 const int inf=0x3f3f3f3f; 11 12 int s[maxn<<1],t[maxm<<3],nxt[maxm<<3],f[maxm<<3],cnt; 13 int dep[maxn<<1]; 14 int n,m,st,ed; 15 16 inline void coredge(int from,int to,int flow) { 17 t[++cnt] = to , f[cnt] = flow, 18 nxt[cnt] = s[from] , s[from] = cnt; 19 } 20 inline void addedge(int from,int to,int flow) { 21 coredge(from,to,flow); 22 coredge(to,from,0); 23 } 24 25 inline bool bfs() { 26 memset(dep,-1,sizeof(dep)); 27 dep[st] = 0; 28 queue<int> q; 29 q.push(st); 30 while( q.size() ) { 31 const int pos = q.front(); q.pop(); 32 for(int at=s[pos];at;at=nxt[at]) 33 if( f[at] && !~dep[t[at]] ) { 34 dep[t[at]] = dep[pos] + 1, 35 q.push(t[at]); 36 } 37 } 38 return ~dep[ed]; 39 } 40 inline int dfs(int pos,int flow) { 41 if( pos == ed ) 42 return flow; 43 int ret = 0 , now = 0; 44 for(int at=s[pos];at;at=nxt[at]) 45 if( f[at] && dep[t[at]] > dep[pos] ) { 46 now = dfs(t[at],min(flow,f[at])); 47 ret += now , flow -= now, 48 f[at] -= now , f[at^1] += now; 49 if( !flow ) 50 return ret; 51 } 52 if( !ret ) 53 dep[pos] = -1; 54 return ret; 55 } 56 inline int dinic() { 57 int ret = 0 , now = 0; 58 while( bfs() ) { 59 while( now = dfs(st,inf) ) 60 ret += now; 61 } 62 return ret; 63 } 64 65 inline int cov(int id,int sta) { 66 return ( id << 1 ) - 1 + sta; 67 } 68 69 inline void init() { 70 for(int i=0;i<=ed;i++) 71 s[i] = 0; 72 cnt = 1; 73 } 74 75 inline int getint() { 76 int ret = 0 , ch = getchar(); 77 while( !isdigit(ch) ) 78 ch = getchar(); 79 while( isdigit(ch) ) 80 ret = ret * 10 + ( ch - '0' ), 81 ch = getchar(); 82 return ret; 83 } 84 85 int main() { 86 while( scanf("%d%d",&n,&m) == 2 ) { 87 init(); 88 st = ( n << 1 ) + 1 , ed = st + 1; 89 for(int i=1;i<=n;i++) { 90 addedge(st,cov(i,0),1); 91 addedge(cov(i,1),ed,1); 92 } 93 for(int i=1,a,b;i<=m;i++) { 94 a = getint() , b = getint(); 95 addedge(cov(a,0),cov(b,1),1); 96 } 97 puts(dinic()==n?"YES":"NO"); 98 } 99 100 return 0; 101 }
T2:
链接:EZOJ_Alpha:P1080

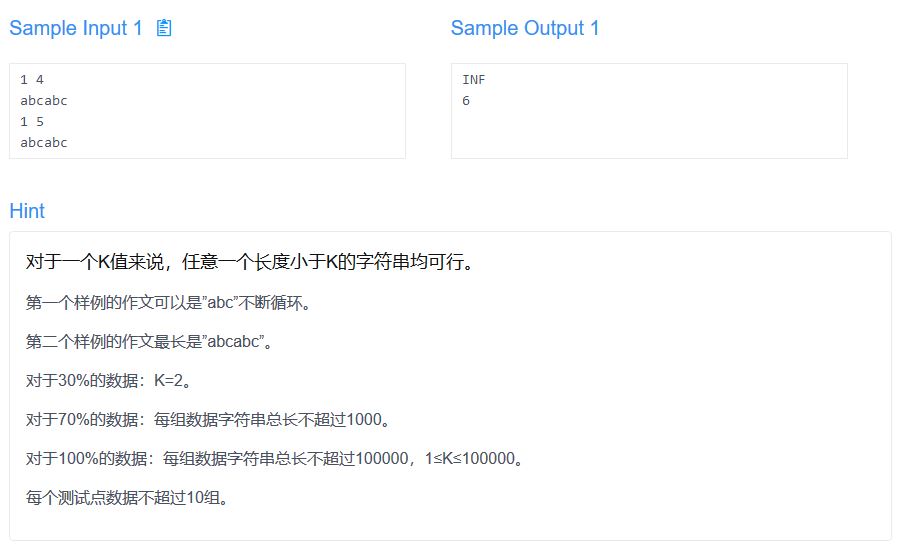
首先,在答案串中一个长度为k+1的子串一定可以通过两个在母串中存在的长度为k的子串重复k-1位生成。
考虑如果不可以这样,即不能生成,这样的话可能是k=5,aac,cddd组成aacddd这样的,那么,acddd在源串中没有存在过,不行。
如果形式化地证明地话:
1.两个长度为k的串重复k-1位,那么截取中间部分那一段就不是源串子串,不行。
2.长度为k+1的串由长度小于k的串重复少于k-1位组成,那么中间那段仍然不是源串子串,不行。(画出图来就明白了)
这样的话可用的拼接的串就是有1e5个,我们可以先对其进行哈希,然后在图上拓扑排序判环顺便求最长链。
这题在考试的时候我没想出来,一开始想SAM统计right什么的,发现这样会把SAM卡成n^2,不可做。然后想SA统计hight什么的,仍旧不可做,弃坑写T3。
写完T3回来发现有k=2的30分floyd可以写,写完走人。
考场30分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define debug cout 6 using namespace std; 7 const int maxn=1e5+1e2,maxd=30; 8 9 char in[maxn]; 10 int g[maxd][maxd],can[maxd][maxd],vis[maxd],app[maxd]; 11 int mxl,n,k,len; 12 13 inline void floyd() { 14 for(int k=1;k<=26;k++) 15 for(int i=1;i<=26;i++) 16 for(int j=1;j<=26;j++) 17 can[i][j] |= ( can[i][k] & can[k][j] ); 18 } 19 20 inline bool judgeinf() { 21 floyd(); 22 for(int i=1;i<=26;i++) 23 if( can[i][i] ) 24 return 1; 25 return 0; 26 } 27 28 inline void dfs(int pos,int dep) { 29 vis[pos] = 1; 30 mxl = max( mxl , dep ); 31 for(int i=1;i<=26;i++) 32 if( g[pos][i] && !vis[i] ) 33 dfs(i,dep+1); 34 vis[pos] = 0; 35 } 36 37 inline int cov(int x) { 38 return x - 'a' + 1; 39 } 40 inline void init() { 41 memset(g,0,sizeof(g)); 42 memset(can,0,sizeof(can)); 43 memset(app,0,sizeof(app)); 44 mxl = 0; 45 } 46 47 int main() { 48 while( scanf("%d%d",&n,&k) == 2 ) { 49 if( k != 2 ) { 50 puts("INF"); 51 continue; 52 } 53 init(); 54 for(int i=1;i<=n;i++) { 55 scanf("%s",in+1); 56 len = strlen(in+1); 57 for(int i=1;i<=len;i++) 58 app[cov(in[i])] = 1; 59 for(int i=1;i<len;i++) { 60 can[cov(in[i])][cov(in[i+1])] = g[cov(in[i])][cov(in[i+1])] = 1; 61 } 62 } 63 if( judgeinf() ) 64 puts("INF"); 65 else { 66 for(int i=1;i<=26;i++) 67 if( app[i] ) 68 dfs(i,1); 69 printf("%d ",mxl); 70 } 71 } 72 return 0; 73 }
考后AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<queue> 6 #include<map> 7 #define lli long long int 8 #define debug cout 9 using namespace std; 10 const int maxn=1e5+1e2,base=233,mod[2]={1000000009,1000000007}; 11 12 struct Node { 13 lli h,t; 14 Node(lli hh=0,lli tt=0) { 15 h = hh , t = tt; 16 } 17 lli id() const { 18 return h / 10000; 19 } 20 friend bool operator < (const Node &a,const Node &b) { 21 return a.h != b.h ? a.h < b.h : a.t < b.t; 22 } 23 }; 24 map<Node,int> cov[maxn]; 25 lli hsh[maxn][2],pows[maxn][2]; 26 int dis[maxn],deg[maxn],nxt[maxn][27],vis[maxn]; 27 char in[maxn]; 28 int ed[maxn]; 29 int n,k,ans,cnt; 30 31 inline void gen(int len) { 32 pows[0][0] = pows[0][1] = 1; 33 hsh[0][0] = hsh[0][1] = 0; 34 for(int i=1;i<=len;i++) 35 for(int j=0;j<2;j++) { 36 hsh[i][j] = ( hsh[i-1][j] * base + in[i] - 'a' + 1) % mod[j]; 37 pows[i][j] = pows[i-1][j] * base % mod[j]; 38 } 39 } 40 41 inline Node SegmentHsh(int st,int ed) { // returning hash Node in range [st,ed] 42 --st; 43 lli h = ( ( hsh[ed][0] - hsh[st][0] * pows[ed-st][0] ) % mod[0] + mod[0] ) % mod[0]; 44 lli t = ( ( hsh[ed][1] - hsh[st][1] * pows[ed-st][1] ) % mod[1] + mod[1] ) % mod[1]; 45 return Node(h,t); 46 } 47 inline Node SegmentWord(int st,int ed,int x) { // returning Segment [st,ed] + x 48 Node Seg = SegmentHsh(st,ed); 49 Seg.h = ( Seg.h * base + x ) % mod[0], 50 Seg.t = ( Seg.t * base + x ) % mod[1]; 51 return Seg; 52 } 53 54 inline int query(const Node &a) { 55 int iid = a.id(); 56 return cov[iid].find(a) == cov[iid].end() ? 0 : cov[iid][a]; 57 } 58 inline void insert(const Node &a) { 59 int iid = a.id(); 60 if( cov[iid].find(a) != cov[iid].end() ) 61 return; 62 cov[iid][a] = ++cnt; 63 } 64 65 inline void insert_all() { 66 for(int i=1;i<=n;i++) { 67 for(int j=ed[i-1]+k-1;j<ed[i];j++) { 68 insert(SegmentHsh(j-k+1,j)); 69 } 70 } 71 } 72 73 inline void find_next() { 74 for(int i=1;i<=n;i++) 75 for(int j=ed[i-1]+k-1;j<ed[i];j++) { 76 Node now = SegmentHsh(j-k+1,j); 77 int id = query(now); 78 if( vis[id] ) 79 continue; 80 vis[id] = 1; 81 for(int w=1;w<=26;w++) { 82 Node nw = SegmentWord(j-k+2,j,w); 83 int nid = query(nw); 84 if( nid ) { 85 ++deg[nid]; 86 nxt[id][w] = nid; 87 } 88 } 89 } 90 } 91 92 inline void topo() { 93 int full = 0; 94 queue<int> q; 95 for(int i=1;i<=cnt;i++) 96 if( !deg[i] ) { 97 dis[i] = 1 , 98 q.push(i); 99 } 100 while( q.size() ) { 101 const int pos = q.front(); q.pop(); ++full; 102 ans = max( ans , dis[pos] ); 103 for(int i=1;i<=26;i++) 104 if( nxt[pos][i] ) { 105 dis[nxt[pos][i]] = max( dis[nxt[pos][i]] , dis[pos] + 1 ); 106 if( !--deg[nxt[pos][i]] ) 107 q.push(nxt[pos][i]); 108 } 109 } 110 if( full < cnt ) 111 puts("INF"); 112 else 113 printf("%d ",ans+k-1); 114 } 115 116 inline void getin() { 117 ed[0] = 1; 118 for(int i=1;i<=n;i++) { 119 scanf("%s",in+ed[i-1]); 120 ed[i] = ed[i-1] + strlen(in+ed[i-1]); 121 } 122 } 123 124 inline void init() { 125 for(int i=0;i<maxn;i++) 126 cov[i].clear(); 127 memset(hsh,0,sizeof(hsh)); 128 memset(pows,0,sizeof(pows)); 129 memset(dis,0,sizeof(dis)); 130 memset(deg,0,sizeof(deg)); 131 memset(nxt,0,sizeof(nxt)); 132 memset(vis,0,sizeof(vis)); 133 memset(ed,0,sizeof(ed)); 134 memset(in,0,sizeof(in)); 135 ans = cnt = 0; 136 } 137 138 int main() { 139 while( scanf("%d%d",&n,&k) == 2 ) { 140 init(); 141 getin(); 142 gen(ed[n]-1); 143 insert_all(); 144 find_next(); 145 topo(); 146 } 147 return 0; 148 }
T3:
链接:EZOJ_Alpha:P1082


首先我们看到了30分暴力,禁忌の8重for循环……或者直接DFS。
然后看一下那40分没有限制的怎么写:每个题目只在总分中出现一次,k道题目平分c的总分……这不是高考数学老师讲过的插板法吗?预处理阶乘和逆元然后O(1)计算组合数。
然后我们70分到手了,考虑剩下30分怎么办:
对于有限制的,我们可以枚举哪几个一定超过了限制,然后容斥。
如何计算超过限制后的方案呢?
我一开始想到了让一定超过限制的那些题目单独算,再维护剩下的,发现不可做。
但是,我们可以先钦定超过限制的那些至少是多少,从总数中减去"他们的限制+1"求和,然后再插板。
但是这样超过限制的不能太多,观察到T<=20,可做。
然后我就被WA成80了。
因为预处理时阶乘最大的范围为max(k+c),然后我只跑到了n*2。
简直愚蠢至极。
考场80分代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #define lli long long int 7 #define debug cout 8 using namespace std; 9 const int maxn=1e6+1e2; 10 const int mod=1000000007; 11 12 int id[maxn],siz[maxn],sum[maxn]; 13 vector<int> lim[maxn]; 14 lli facs[maxn<<1],revs[maxn<<1]; 15 lli ans = 1; 16 int n,m,t; 17 18 inline lli fastpow(lli base,int tme) { 19 lli ret = 1; 20 while( tme ) { 21 if( tme & 1 ) 22 ret = ret * base % mod; 23 base = base * base % mod; 24 tme >>= 1; 25 } 26 return ret; 27 } 28 inline void gen() { 29 *revs = *facs = 1; 30 for(int i=1;i<=n<<1;i++) { 31 facs[i] = facs[i-1] * i % mod , 32 revs[i] = revs[i-1] * fastpow(i,mod-2) % mod; 33 } 34 } 35 36 inline lli c(int n,int m) { 37 return facs[n] * revs[m] % mod * revs[n-m] % mod; 38 } 39 40 inline int count(int ss) { 41 int ret = 0; 42 while( ss ) 43 ret++ , 44 ss -= ( ss & -ss ); 45 return ret; 46 } 47 inline int calcsum(int ss,vector<int> lims) { 48 int ret = 0; 49 for(unsigned i=0;i<lims.size();i++) 50 if( ss & ( 1 << i ) ) 51 ret += lims[i]; 52 return ret; 53 } 54 inline lli calcextra(int siz,int full) { 55 return c(full+siz-1,siz-1); 56 } 57 inline lli calc(int siz,int full,vector<int> lims) { 58 lli ret = calcextra(siz,full); 59 int fs = ( 1 << lims.size() ) - 1; 60 for(int ss=1;ss<=fs;ss++) { 61 const int sum = calcsum(ss,lims); 62 if( full - sum >= 0 ) { 63 ret += ( ( count(ss) & 1 ) ? -1 : 1 ) * calcextra(siz,full-sum); 64 ret = ( ret % mod + mod ) % mod; 65 } 66 } 67 return ret; 68 } 69 70 int main() { 71 scanf("%d%d",&n,&m); 72 for(int i=1,k,p;i<=m;i++) { 73 scanf("%d",&k); 74 siz[i] = k; 75 while( k-- ) { 76 scanf("%d",&p); 77 id[p] = i; 78 } 79 scanf("%d",sum+i); 80 } 81 scanf("%d",&t); 82 for(int i=1,r,L;i<=t;i++) { 83 scanf("%d%d",&r,&L); 84 lim[id[r]].push_back(L+1); 85 } 86 gen(); 87 88 for(int i=1;i<=m;i++) 89 ans = ans * calc(siz[i],sum[i],lim[i]) % mod; 90 91 printf("%lld ",ans); 92 93 return 0; 94 }
考后AC代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #include<vector> 6 #define lli long long int 7 #define debug cout 8 using namespace std; 9 const int maxn=1e6+1e2; 10 const int mod=1000000007; 11 12 int id[maxn],siz[maxn],sum[maxn]; 13 vector<int> lim[maxn]; 14 lli facs[maxn<<1],revs[maxn<<1]; 15 lli ans = 1; 16 int n,m,t; 17 18 inline lli fastpow(lli base,int tme) { 19 lli ret = 1; 20 while( tme ) { 21 if( tme & 1 ) 22 ret = ret * base % mod; 23 base = base * base % mod; 24 tme >>= 1; 25 } 26 return ret % mod; 27 } 28 inline void gen() { 29 *revs = *facs = 1; 30 for(int i=1;i<maxn<<1;i++) { 31 facs[i] = facs[i-1] * i % mod , 32 revs[i] = revs[i-1] * fastpow(i,mod-2) % mod; 33 } 34 } 35 36 inline lli c(int n,int m) { 37 return facs[n] * revs[m] % mod * revs[n-m] % mod; 38 } 39 40 inline int count(int ss) { 41 int ret = 0; 42 while( ss ) 43 ret++ , 44 ss -= ( ss & -ss ); 45 return ret; 46 } 47 inline int calcsum(int ss,vector<int> lims) { 48 int ret = 0; 49 for(unsigned i=0;i<lims.size();i++) 50 if( ss & ( 1 << i ) ) 51 ret += lims[i]; 52 return ret; 53 } 54 inline lli calcextra(int siz,int full) { 55 return c(full+siz-1,siz-1); 56 } 57 inline lli calc(int siz,int full,vector<int> lims) { 58 lli ret = calcextra(siz,full); 59 int fs = ( 1 << lims.size() ) - 1; 60 for(int ss=1;ss<=fs;ss++) { 61 const int sum = calcsum(ss,lims); 62 if( full - sum >= 0 ) { 63 ret += ( ( count(ss) & 1 ) ? -1 : 1 ) * calcextra(siz,full-sum); 64 ret = ( ret % mod + mod ) % mod; 65 } 66 } 67 /*if( !ret ) { 68 puts("Fuck you!"); 69 }*/ 70 return ret; 71 } 72 73 int main() { 74 scanf("%d%d",&n,&m); 75 for(int i=1,k,p;i<=m;i++) { 76 scanf("%d",&k); 77 siz[i] = k; 78 while( k-- ) { 79 scanf("%d",&p); 80 id[p] = i; 81 } 82 scanf("%d",sum+i); 83 } 84 scanf("%d",&t); 85 for(int i=1,r,L;i<=t;i++) { 86 scanf("%d%d",&r,&L); 87 lim[id[r]].push_back(L+1); 88 } 89 gen(); 90 91 for(int i=1;i<=m;i++) 92 ans = ans * calc(siz[i],sum[i],lim[i]) % mod; 93 94 printf("%lld ",ans); 95 96 return 0; 97 }
总体来说这次发挥算是比较正常,然而还是犯了一些愚蠢的错误的。下次不要再犯了。另外,心态真的很重要啊。
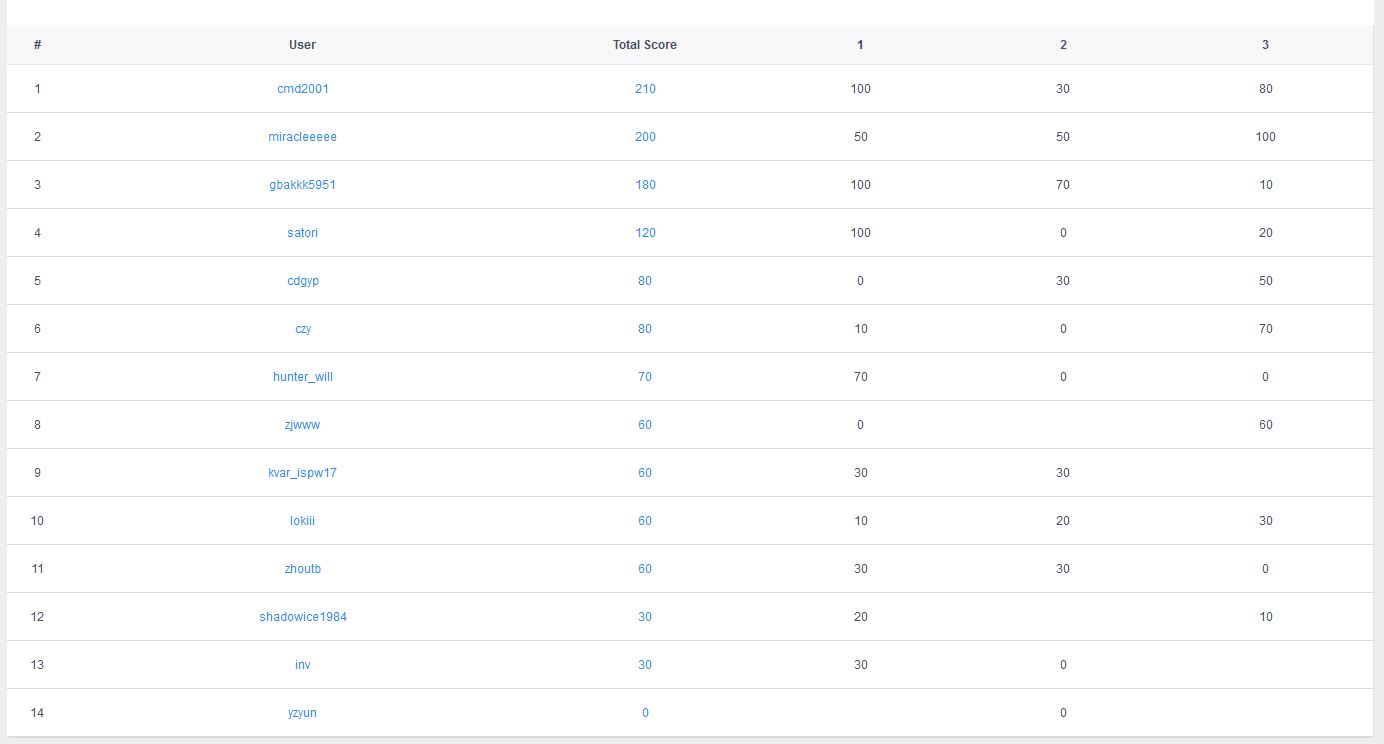
最后补一张排名: