先来一个题面:

题目要我们计算在n*m的点阵中不同的直线有多少条。
显然平行于坐标轴的直线只有n+m条,所以我们只需要考虑不平行于坐标轴的。
我们枚举直线的方向向量(a,b),且令a,b>0,那么每一条这样的直线通过绕垂直轴翻转都能一一对应一条另一方向的直线(显然,自行脑补就行了)。
然后,我们定义一个点(x,y)的前驱为(x−a,y−b),后继为(x+a,y+b),则直线的数量为满足“它本身以及它的前驱在点阵内而它的后继不在点阵内”的点的数量。
就是下面这个式子。
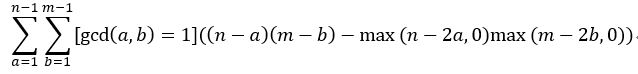
官方的式子就讲到这里了,下面我们来想想这个鬼畜的东西怎么计算。
我们先考虑没有max的那一项,有max的计算方法相同,只是更改一下系数罢了。

对于n-1/d,m-1/d这样的东西,我们可以O(sqrt)地求解。
然后,对于后面乘上的那个东西与μ(d)的积,我们需要找出别的计算方法。

我们可以先线性地筛出μ(d)*d的前缀和,再O(sqrt)地枚举n-1/d,求解这个式子。
对于最后的那个交叉乘项,也这样做,无非就是更复杂一些。
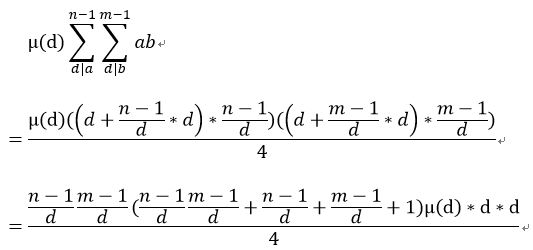
然后发现我们只要预处理出来μ(d)*d*d的前缀和就可以做啦!
最后,原式变成了:
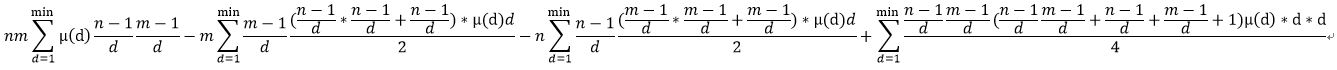
对于第二个式子,我们也可以类似地反演,只是要修改系数。注意只有当a<=n/2且b<=m/2的时候有值,所以需要更改一下计算范围QAQ。最后反演出来大概是这样的。
注意此时的min’=min(a/2,b/2),然而n、m还得带入原来的值。也就是说,我们缩小了d的枚举范围却没有修改nm的范围。(注意如果直接令n/=2,m/=2会wa。这很显然,自己想想为什么)
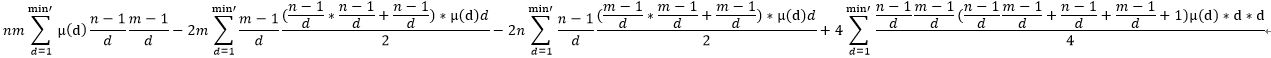
最后上代码:

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 #define lli long long int 6 #define debug cout 7 using namespace std; 8 const int maxn=4e5+1e2; 9 const int MOD=1<<30; 10 11 lli sum[maxn][3]; 12 lli ans; 13 14 inline lli mod(lli x) { 15 return (x%MOD+MOD)%MOD; 16 } 17 18 inline void gen() { 19 static int mu[maxn],prime[maxn],cnt; 20 static bool vis[maxn]; 21 22 mu[1]=1; 23 for(int i=2;i<maxn;i++) { 24 if(!vis[i]) { 25 prime[++cnt]=i; 26 mu[i]=-1; 27 } 28 for(int j=1;j<=cnt&&(lli)i*prime[j]<maxn;j++) { 29 vis[i*prime[j]]=1; 30 if(i%prime[j]) 31 mu[i*prime[j]]=-mu[i]; 32 else { 33 mu[i*prime[j]]=0; 34 break; 35 } 36 } 37 } 38 for(int i=1;i<maxn;i++) { 39 sum[i][0]=sum[i-1][0]+mu[i]; 40 sum[i][1]=sum[i-1][1]+mu[i]*i; 41 sum[i][2]=sum[i-1][2]+mu[i]*i*i; 42 } 43 } 44 45 inline lli calc_g(int n,int m) { 46 lli ret=0; 47 int lim=min(n,m); 48 for(int i=1,j=1;i<=lim;i=j+1) { 49 j=min(n/(n/i),m/(m/i)); 50 ret=mod( ret + mod( (sum[j][0]-sum[i-1][0])*(n/i)*(m/j) ) ); 51 } 52 return mod( ret ); 53 } 54 inline lli calc_mul(int n,int m) { 55 lli ret=0; 56 int lim=min(n,m); 57 for(int i=1,j=1;i<=lim;i=j+1) { 58 j=min(n/(n/i),m/(m/i)); 59 lli len=n/i,bin=m/j; 60 lli step=mod(bin*(bin+1)>>1); 61 ret += (sum[j][2]-sum[i-1][2]) * mod( mod(len*(len+1)>>1) * step ); 62 ret = mod(ret); 63 } 64 return mod( ret ); 65 } 66 inline lli calc_add(int n,int m,int fn,int fm) { 67 lli ret=0; 68 int lim=min(n,m); 69 for(int i=1,j=1;i<=lim;i=j+1) { 70 j=min(n/(n/i),m/(m/i)); 71 lli mxi = n/i , mxj = m/j; 72 lli stepi = mod( mxi*(mxi+1)>>1 ); 73 lli stepj = mod( mxj*(mxj+1)>>1 ); 74 ret += (sum[j][1]-sum[i-1][1])*( stepi*fm*mxj + stepj*fn*mxi ); 75 ret = mod(ret); 76 } 77 return mod( ret ); 78 } 79 inline void getans(int n,int m) { 80 ans=0; 81 ans += ( calc_g(n,m) - calc_g(n/2,m/2) )*n*m % MOD; 82 ans%=MOD; 83 ans += ( calc_add(n/2,m/2,n,m)*2 - calc_add(n,m,n,m) ) % MOD; 84 ans%=MOD; 85 ans += ( calc_mul(n,m) - calc_mul(n/2,m/2)*4 ) % MOD; 86 ans%=MOD; 87 ans<<=1; 88 ans+=n+m; 89 ans = mod(ans); 90 } 91 int nextchar() { 92 static char pool[1<<20],*st=pool+(1<<20),*ed=pool+(1<<20); 93 if(st==ed) ed = pool + fread(st=pool,1,1<<20,stdin); 94 return *st++; 95 } 96 inline int getint() { 97 int ret=0,fix=1; 98 char ch=nextchar(); 99 while(ch<'0'||ch>'9'){if(ch=='-')fix=-1; ch=nextchar();} 100 while(ch>='0'&&ch<='9') 101 ret=ret*10+(ch-'0'), 102 ch=nextchar(); 103 return ret*fix; 104 } 105 106 int main() { 107 gen(); 108 static int t,n,m; 109 110 t=getint(); 111 while(t--) { 112 n=getint(),m=getint(); 113 getans(n,m); 114 printf("%lld ",ans); 115 } 116 117 return 0; 118 }
