[SCOI2012] 滑雪（最小树形图）

题意

给定一张图，每个节点有高度，一个点只能到达高度不大于它的其他点，求从1号节点出发所能到达的节点数（包括自己）以及这些节点的最小树形图（以1为根且可以到达其他点的树）的边权和

思路

从1出发能到达的点用一遍bfs即可求出，然后就相当于求剩下节点的最小树形图

如果所有边都是无向边，显然就是求最小生成树，而现在放到有向图里面，可以用朱刘算法，但是O((VE))会超时，于是我们考虑一下这张图的特性

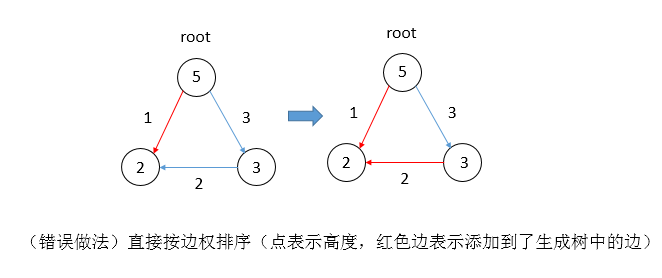
由于连边是由高度决定的，高度相等的连无向边，所以一定没有一个有向边组成的环。想一下为什么不能直接使用kruskal求最小生成树？因为这样的生成树可能会有从高度低的指向高度高的边（因为把有向边当成无向边了

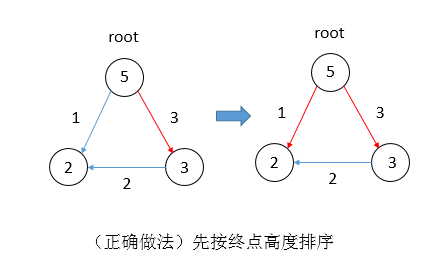
所以对kruskal的排序进行改进，以有向边终点高度为第一关键字从大到小排序，以边权为第二关键字从小到大排序，就可以直接使用kruskal了

为什么这样做是正确的？

可以这样理解：既然一个点早晚要被加入这个生成树中，那么将高的点排在前面不会影响正确性；而且高的先加入就不会出现连反的情况了（矮的先加入的话可能到时候高的想要加入就必须要反向连边才行，如下图）

Code:

#include<bits/stdc++.h>
#define N 100005
#define M 1000005
using namespace std;
typedef long long ll;
const ll INF = 10000000000000000;
int n,m,h[N],fa[N];
int ans1;ll ans2;
bool vis[N];

struct E {int u,v;ll w;} e[M<<1];
struct Edge {int next,to;ll dis;}edge[M<<1];
int head[N],cnt=1;
void add_edge(int from,int to,ll dis)
{
    edge[++cnt].next=head[from];
    edge[cnt].to=to;
    edge[cnt].dis=dis;
    head[from]=cnt;
}
template <class T>
void read(T &x)
{
    char c;int sign=1;
    while((c=getchar())>'9'||c<'0') if(c=='-') sign=-1; x=c-48;
    while((c=getchar())>='0'&&c<='9') x=(x<<1)+(x<<3)+c-48; x*=sign;
}
int find(int x) {return x==fa[x] ? x : fa[x]=find(fa[x]);}
bool cmp(E a,E b) {return h[a.v]!=h[b.v] ? h[a.v]>h[b.v] : a.w<b.w;}
void bfs()
{
    queue<int> q;
    q.push(1);cnt=0;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        if(vis[u]) continue;
        vis[u]=1;
        ++ans1;
        for(int i=head[u];i;i=edge[i].next)
        {
            int v=edge[i].to;
            if(h[v]<h[u])
            {
                e[++cnt].u=u;
                e[cnt].v=v;
                e[cnt].w=edge[i].dis;
                if(vis[v]) continue;
                q.push(v);
            }
            else if(h[v]==h[u])
            {
                if(vis[v]) continue;
                e[++cnt].u=u;
                e[cnt].v=v;
                e[cnt].w=edge[i].dis;
                q.push(v);
            }
        }
    }
}
void kruskal()
{
    sort(e+1,e+cnt+1,cmp);
    for(int i=1;i<=n;++i) fa[i]=i;
    int used=0;
    for(int i=1;i<=cnt;++i)
    {
        int fu=find(e[i].u),fv=find(e[i].v);
        if(fu!=fv)
        {
            fa[fu]=fv;
            ans2+=e[i].w;
            if(++used==ans1-1) break;
        }
    }
}
int main()
{
    read(n);read(m);
    for(int i=1;i<=n;++i) read(h[i]);
    for(int i=1;i<=m;++i)
    {
        int x,y;ll z;
        read(x);read(y);read(z);
        add_edge(x,y,z);
        add_edge(y,x,z);
    }
    bfs();
    kruskal();
    cout<<ans1<<' '<<ans2<<endl;
    return 0;
}