1、无约束最优化问题

求解此问题的方法方法分为两大类:最优条件法和迭代法。
2、最优条件法

我们常常就是通过这个必要条件去求取可能的极小值点,再验证这些点是否真的是极小值点。当上式方程可以求解的时候,无约束最优化问题基本就解决了。实际中,这个方程往往难以求解。这就引出了第二大类方法:迭代法。
最优条件法:最小二乘估计
3、迭代法
(1)梯度下降法(gradient descent),又称最速下降法(steepest descent)
梯度下降法是求解无约束最优化问题的一种最常用的方法。梯度下降法是迭代算法,每一步需要求解目标函数的梯度向量。
必备条件:函数f(x)必须可微,也就是说函数f(x)的梯度必须存在
优点:实现简单
缺点:最速下降法是一阶收敛的,往往需要多次迭代才能接近问题最优解。
算法A.1(梯度下降法)
输入:目标函数f(x),梯度函数g(x)=▽f(x),计算精度ε;
输出:f(x)的极小点x*

总结:选取适当的初值x(0),不断迭代,更新x的值,进行目标函数的极小化,直到收敛。由于负梯度方向是使函数值下降最快的方向,在迭代的每一步,以负梯度方向更新x的值,从而达到减少函数值的目的。
λk叫步长或者学习率;梯度方向gk=g(x(k))是x=x(k)时目标函数f(x)的一阶微分值。


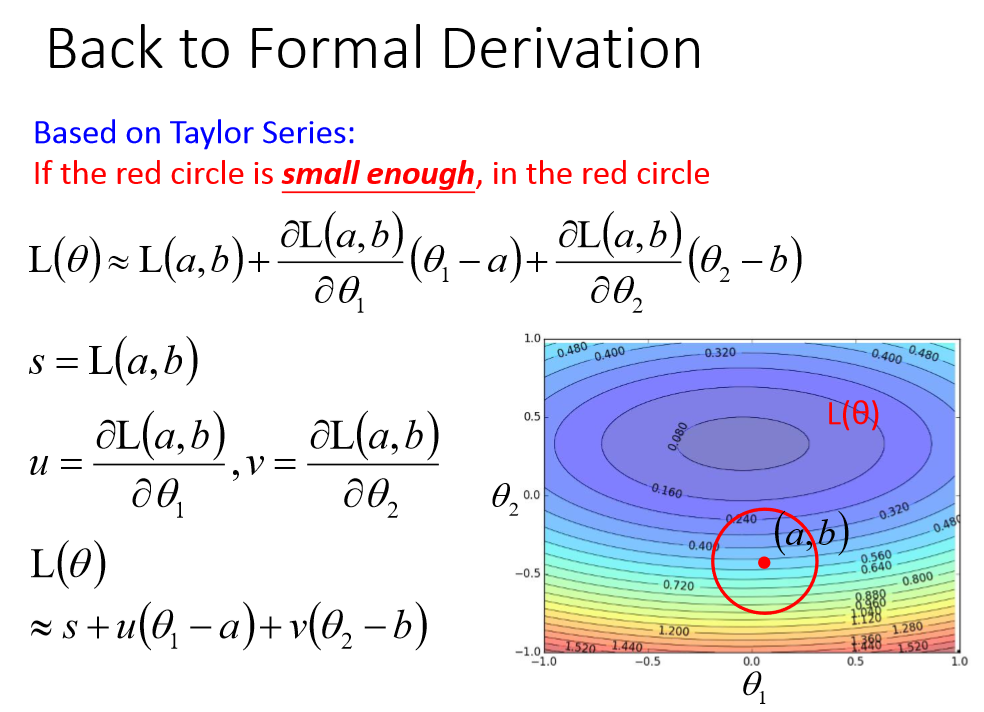

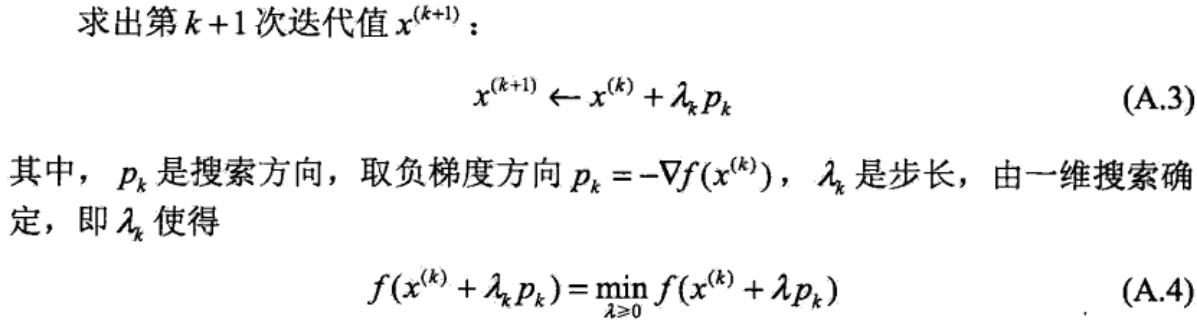
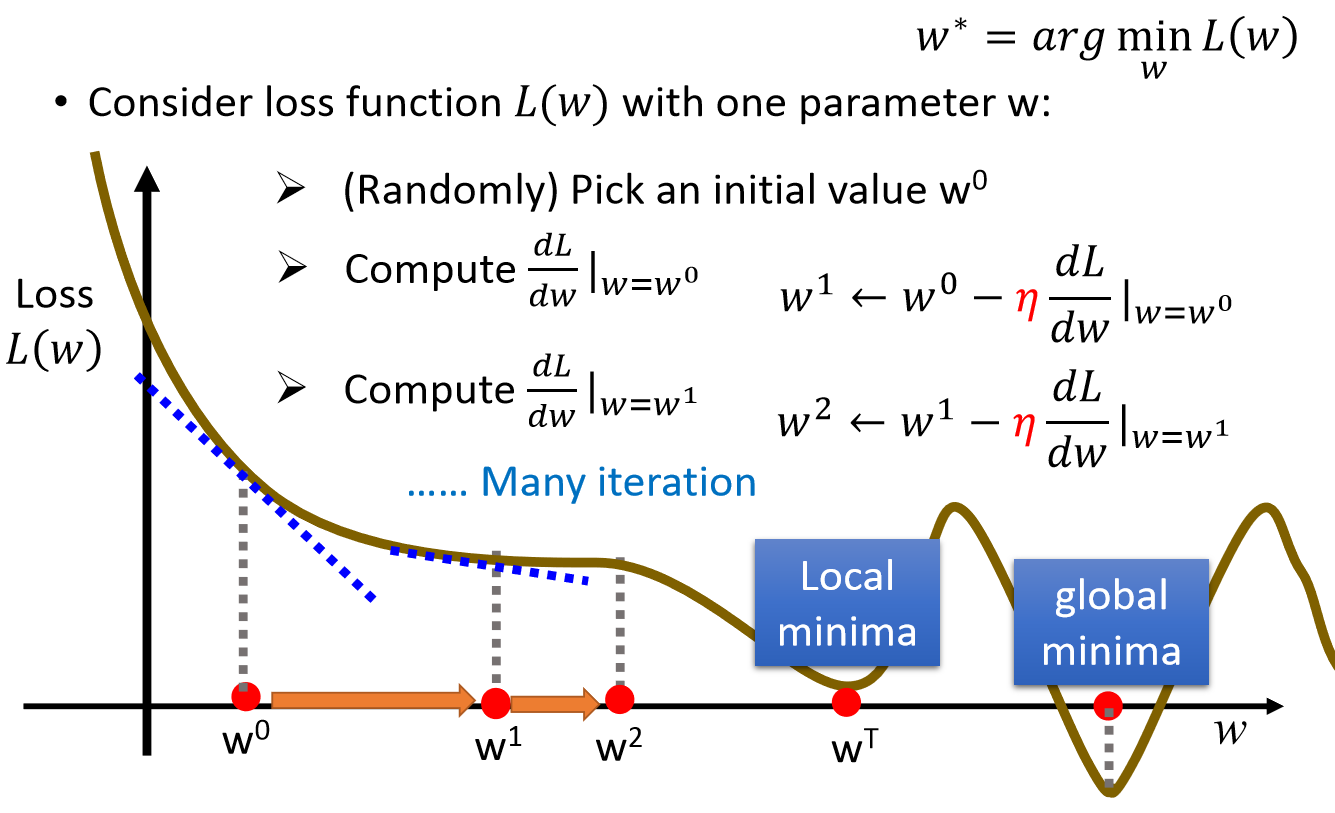

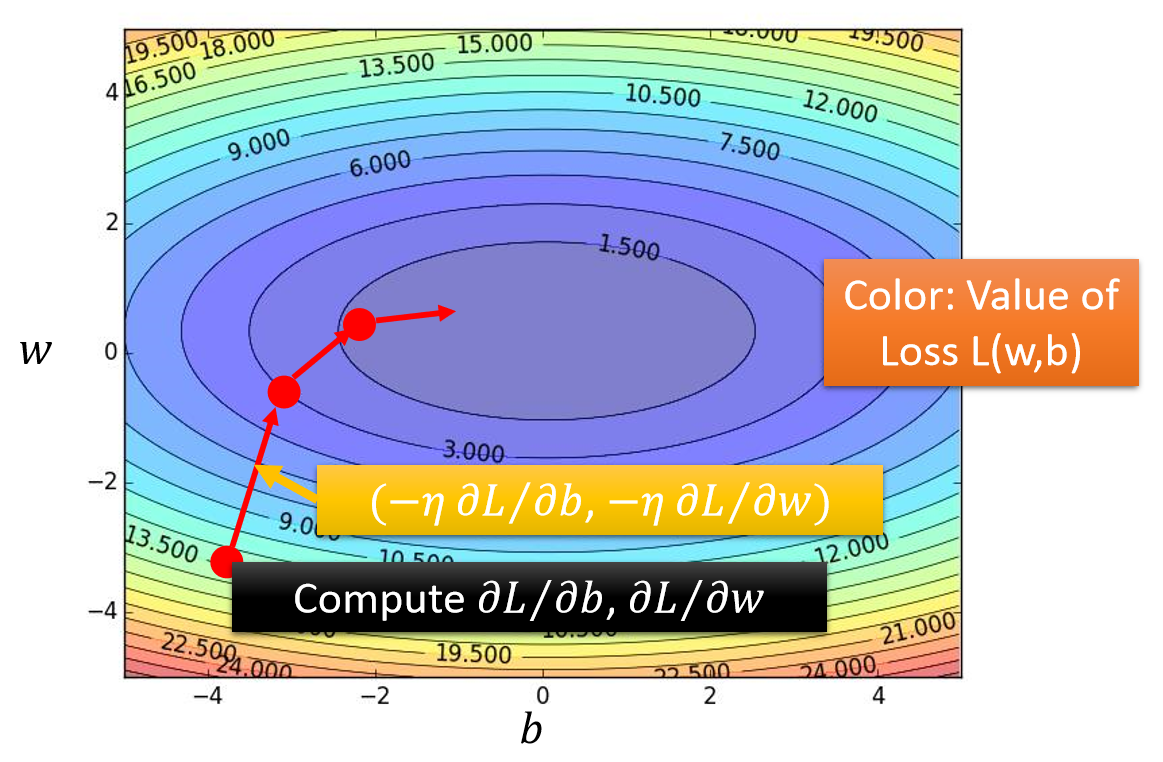
学习率/步长 λ 的确定:
当f(x)的形式确定,我们可以通过求解这个一元方程来获得迭代步长λ。当此方程形式复杂,解析解不存在,我们就需要使用“一维搜索”来求解λ了。一维搜索是一些数值方法,有0.618法、Fibonacci法、抛物线法等等,这里不详细解释了。
在实际使用中,为了简便,也可以使用一个预定义的常数而不用一维搜索来确定步长λ。这时步长的选择往往根据经验或者通过试算来确定。步长过小则收敛慢,步长过大可能震荡而不收敛。如下图:
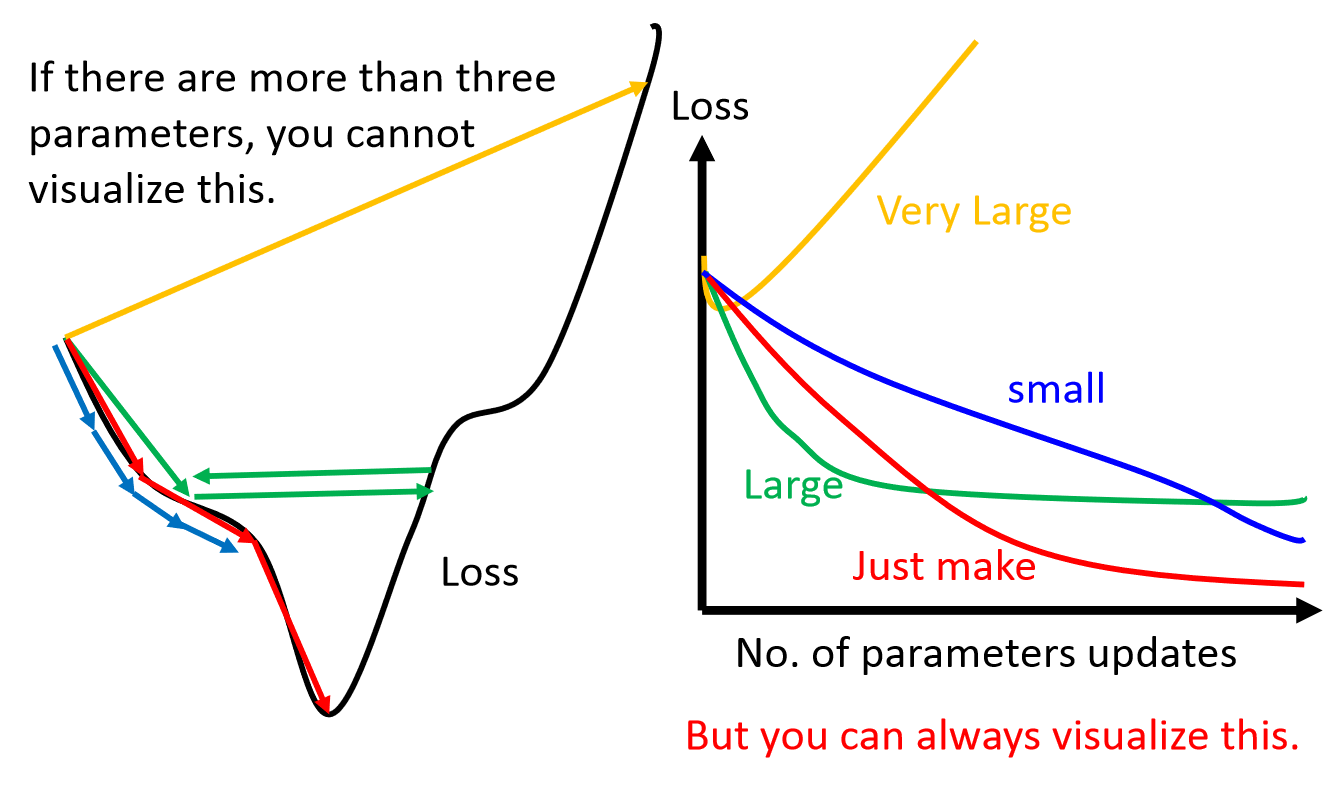
当目标函数是凸函数时,梯度下降法的解是全局最优解。但是,一般情况下,往往不是凸函数,所以其解不保证是全局最优解。梯度下降法的收敛速度也未必是最快的。
梯度下降的算法调优
在使用梯度下降时,需要进行调优。哪些地方需要调优呢?
1. 算法的步长选择。在前面的算法描述中,我提到取步长为1,但是实际上取值取决于数据样本,可以多取一些值,从大到小,分别运行算法,看看迭代效果,如果损失函数在变小,说明取值有效,否则要增大步长。前面说了。步长太大,会导致迭代过快,甚至有可能错过最优解。步长太小,迭代速度太慢,很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。
2. 算法参数的初始值选择。 初始值不同,获得的最小值也有可能不同,因此梯度下降求得的只是局部最小值;当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险,需要多次用不同初始值运行算法,关键损失函数的最小值,选择损失函数最小化的初值。
3.归一化。由于样本不同特征的取值范围不一样,可能导致迭代很慢,为了减少特征取值的影响,可以对特征数据归一化,也就是对于每个特征x,求出它的期望和标准差std(x),然后转化为:![]()
这样特征的新期望为0,新方差为1,迭代次数可以大大加快。
(2)梯度下降法大家族(BGD、SGD、MBGD)
- 批量梯度下降法(Batch Gradient Descent)
批量梯度下降法(Batch Gradient Descent, BGD)是梯度下降法的最原始的形式,其特点就是每一次训练迭代都需要利用所有的训练样本,其表达式为:
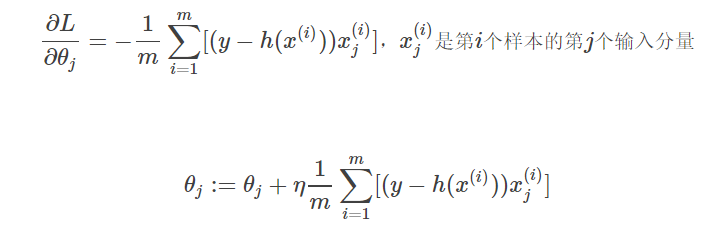
可以发现,对于每一个参数的更新都需要利用到所有的m个样本,这样会导致训练速度随着训练样本的增大产生极大地减慢,不适合于大规模训练样本的场景,但是,其解是全局最优解,精度高。
- 随机梯度下降法(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本来求梯度。

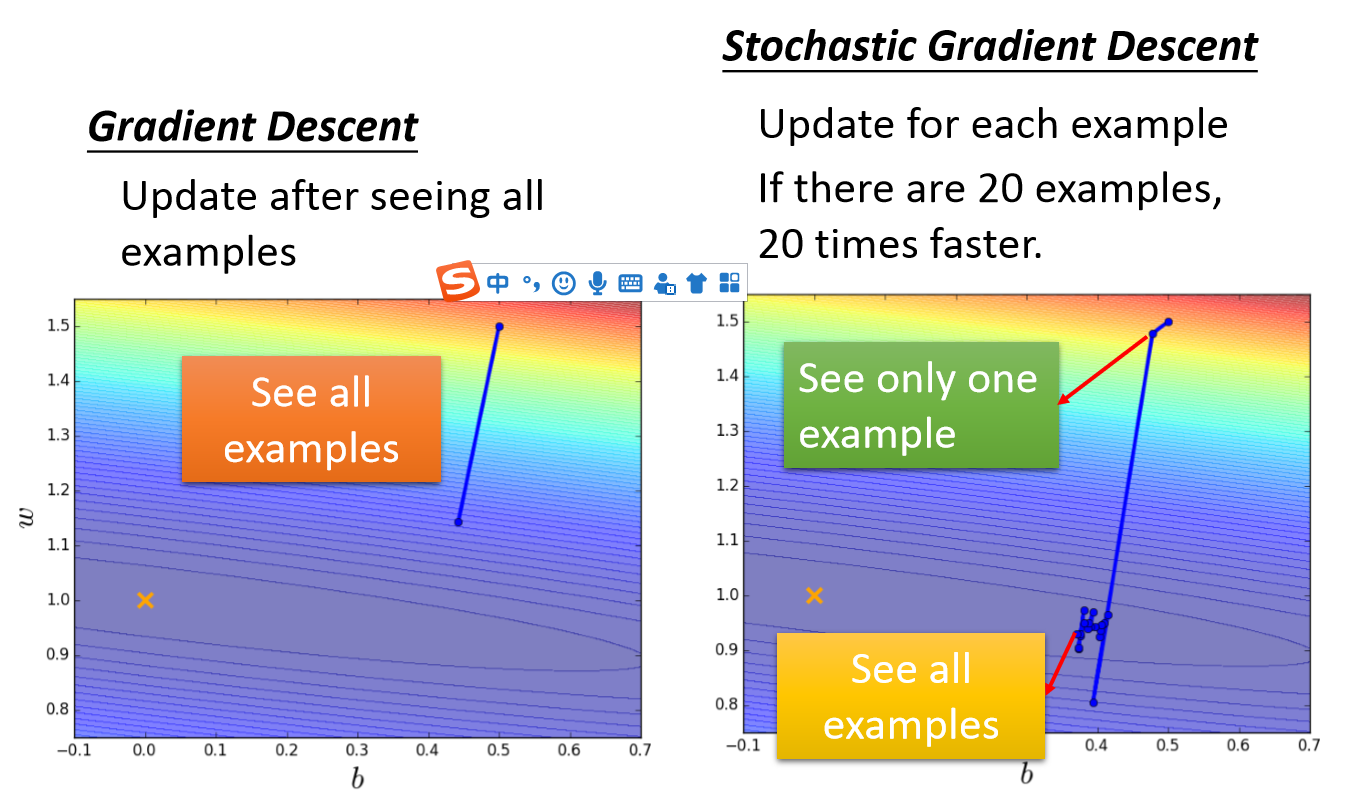
随机梯度下降法 和 批量梯度下降法 是两个极端,一个用一个样本来梯度下降,一个采用所有数据来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。对于准确度来说,随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。
那么,有没有一个中庸的办法能够结合两种方法的优点呢?有!这就是小批量梯度下降法。
- 小批量梯度下降法(Mini-Batch Gradient Descent)
小批量梯度下降法是批量梯度下降法和随机梯度下降法的折衷,也就是对于m个样本,我们采用x个样本来迭代,1<x<m。一般可以取x=10,当然根据样本的数据,可以调整这个x的值。其基本特点就是每一次训练迭代在训练集中随机采样batch_size个样本。对应的更新公式是:

这个方法在深度学习的网络训练中有着广泛地应用,因为其既有较高的精度,也有较快的训练速度。
- Adagrad(Adaptive Learning Rates)
Adagrad是解决不同参数应该使用不同的更新速率的问题。Adagrad自适应地为各个参数分配不同学习率的算法。通过每个参数的学习率除以它之前导数的均方根来调节学习率。公式如下:


公式化简:

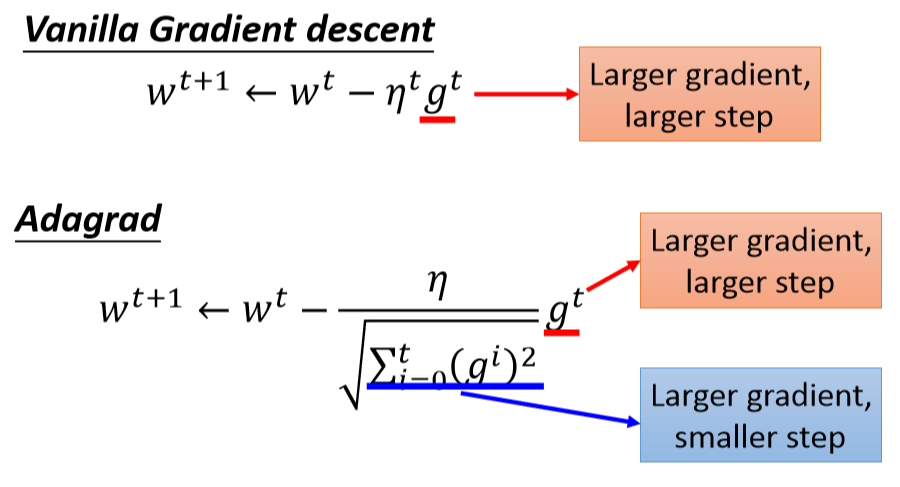
但是我们发现一个现象,本来应该是随着gradient的增大,我们的学习率是希望增大的,也就是图中的gt;但是与此同时随着gradient的增大,我们的分母是在逐渐增大,也就对整体学习率是减少的,这是为什么呢?
这是因为随着我们更新次数的增大,我们是希望我们的学习率越来越慢。因为我们认为在学习率的最初阶段,我们是距离损失函数最优解很远的,随着更新的次数的增多,我们认为越来越接近最优解,于是学习速率也随之变慢。
转载:https://blog.csdn.net/hanlin_tan/article/details/47376237
http://www.cnblogs.com/pinard/p/5970503.html
参考:李航《统计学习方法》、李宏毅《机器学习》