1. threshold临界点:当training data足够多的时候,便会达到临界点, 使得神经元释放output
2. Activation functions: 激励函数,在神经网络中,利用激励函数可以把线性函数转化为平滑的曲线型函数
sigmoid函数: 当x=0时,y=0.5
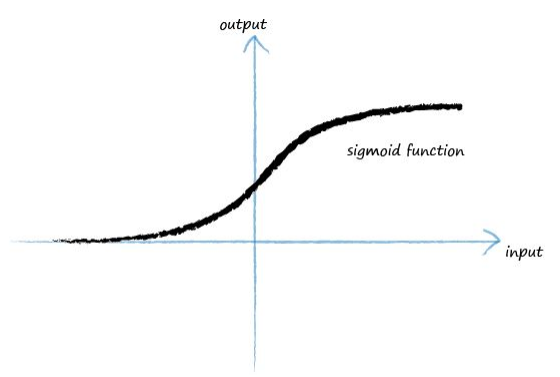
在开始阶段,会有很多input进入神经元:
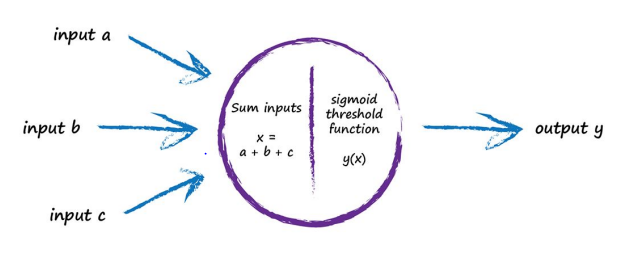
在input数量不足时,sigmoid函数会一直压制output,直到pass临界点
3. weight, 每条路径都有一个weight,weight可以增强input,也可以减弱input,用来和input数值相乘
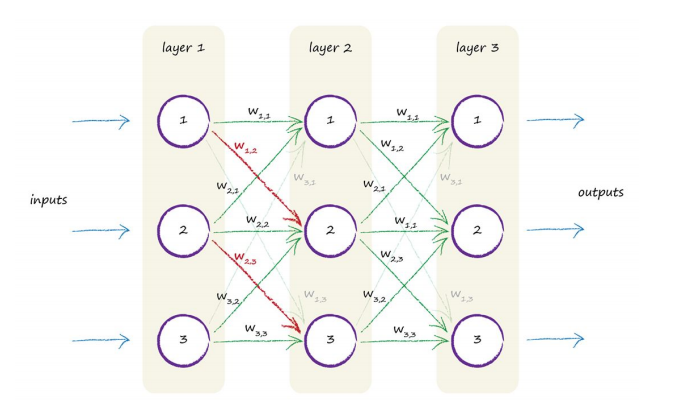
例如:在下图中,计算layer2的output,首先1->1, 2->1,两条路径,所以x = 1.0*0.9 + 0.5*0.3, 然后带入sigmoid函数,算出output为0.7408
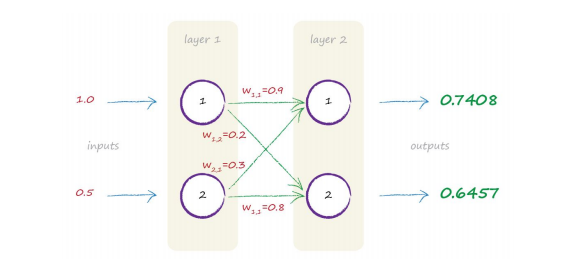
矩阵相乘,来自动计算outputs
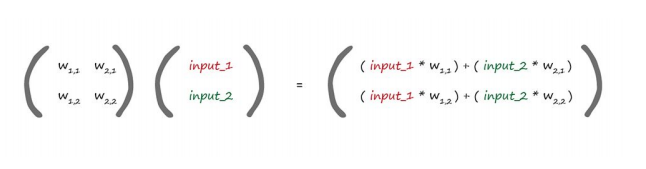
待续。。。。
------------------------------------------------------------------------------------分割线---------------------------------------------------------------------------
多层terms:
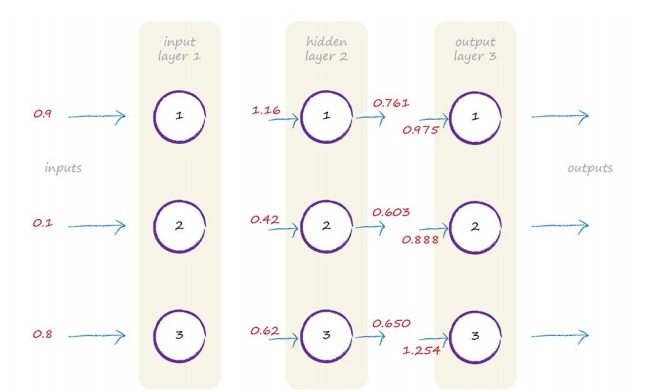
每当计算出一次output的时候,和training data进行对比, 得到误差,然后用之前的方法来完善神经网络。
如果有大于1条的weight 来得出output, 得出的error, e = (t-o),要按照weight贡献度的比例来进行修正分配。
Backpropagating(反向传播算法):用error反向modify ,反向按比例输出Error(hidden)
如图:
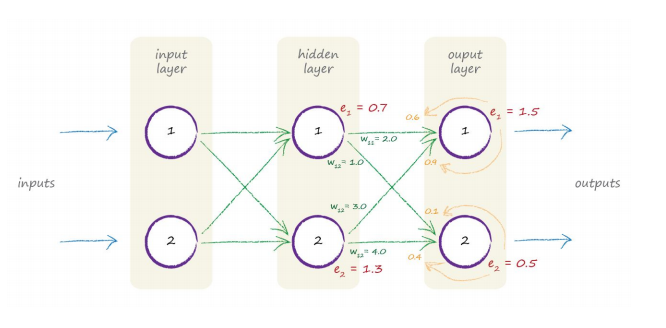
通过反向遍历每条路径占的比例,分配相对的e值,然后用e去modify每条路径的weight
引用原文:Neural networks learn by refining their link weights.
This is guided by the error- the difference between the right answer given by the training data and their actual output: e = t - o
用矩阵相乘来实现自动化反向传播,给机器语言提供了实现的可能性(w为每条路径的weight):
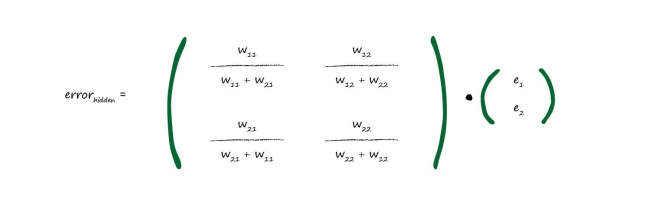
第二种相对简单的矩阵相乘来实现反向传播遍历,由于每条路径的weight是不同的,同一个output对应的子节点.
我们选取weight值相对占比重大的来节约计算时间,但失去精度, 把矩阵的每一行换成每一列,名字叫transposing a matrix(转置矩阵)
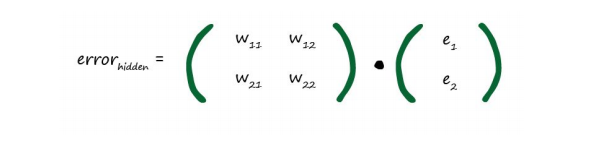
Take a well deserved break~! :-)
在了解如何去更新神经网络中的那些weights,先看一下梯度下降(Gradient Descent)这个数学术语:
比如我们在一座大山上的某处位置,由于我们不知道怎么下山,于是决定走一步算一步,也就是在每走到一个位置的时候,求解当前位置的梯度,沿着梯度的负方向,也就是当前最陡峭的位置向下走一步,然后继续求解当前位置梯度,向这一步所在位置沿着最陡峭最易下山的位置走一步。这样一步步的走下去,一直走到觉得我们已经到了山脚。当然这样走下去,有可能我们不能走到山脚,而是到了某一个局部的山峰低处。可以看出,梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
在遇到复杂的机器学习算法时,比如去modify error时,可以考虑用梯度下降法,逐步的试探,分析问题,得出的答案不一定是最精确的,但是也是有效的答案
举个栗子:
假设现在有一个复杂的算法y = (x-1)^2 + 1, 在这个方程式中,y是神经网络中所谓的error,所以我们要想办法找到x的值=>在神经网络中,也就是weight的值,去最小化所谓的error,首先看一下这个方程式的图:

在这个方程式中,如果不知道如何求得x的值,可以用梯度下降法,逐步的去用测试的x值进行modify,不停地有规律的modify x的值,直到x的迭代变化变得非常小的时候,我们就十分接近最小的y值了
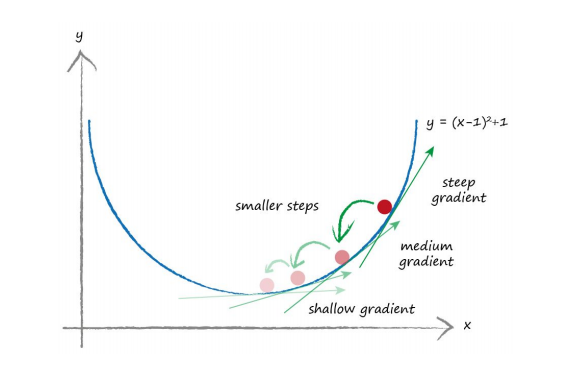
在真实的神经网络算法中,每个error有可能有不同的很多的weight路径,也就是说有很多变量,这时候梯度下降方法可以逐渐找到答案。。
同时,在神经网络中,会有很多坑,就像山会有很多山谷一样,所以我们在做梯度下降时,要选择不用的X起点,去找到真正的最小值: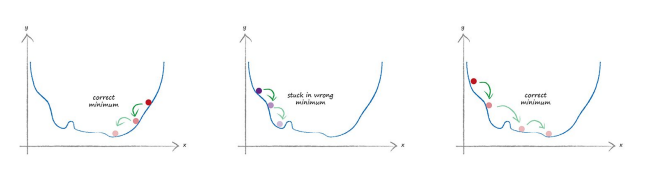
待续。。。
------------------------------------------------------------------------------------分割线---------------------------------------------------------------------------
calculus(微积分),用来表示变量之间的关系,所以在神经网络用来表示error function和link weight 之间的关系:
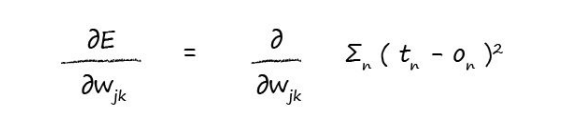
tn-on的平方,也就是误差的平方,为什么要用平方表示呢?
(目标值-实际值)的平方。我们采用这种函数测量误差主要是基于如下几点:
1.梯度下降法中求解斜率的时候比较容易。
2.这个误差函数时平滑而连续的,能够很好的发挥梯度下降法的优势
3.当靠近最小值的时候,梯度值越来越小。这意味着我们将使用平滑的步长靠近最小值,从而避免越过最小值的风险。
接下来通过微积分推倒,以及sigmoid的变形:

得出最终公式,也就是Error和weight之间的关系:


对于output,input,关于trainingdata的要求,首先trainingdata要符合逻辑,能真实的处理实际问题; 其次每个slape不能调度过大; 然后zero值很可能会导致整个机器学习的神经网络失去功能;hidden layers的link weights需要是随机的,并且跨度小的; 通常input值都在0.01-0.99, 或者-1.0 到+1.0; 通常output都在0以上,1以下,一个比较好的range是0.01-0.99。
接下来用python写一个training session,做图像识别,请见下章
