1、结构
set和multiset会根据特定的排序原则将元素排序。两者不同之处在于,multisets允许元素重复,而set不允许重复。

只要是assignable、copyable、comparable(根据某个排序准则)的型别T,都可以成为set或者multisets的元素。如果没有特别的排序原则,采用默认的less,已operator < 对元素进行比较,以便完成排序。
排序准则必须遵守以下原则:
- 必须是“反对称的”,对operator <而言,如果x < y为真,y<x为假。
- 必须是“可传递的”,对operator <而言,如果x<y为真,y<z为真,那么x<z也为真。
- 必须是“非自反的”,对operator<而言,x<x永远为假。
2、能力
和所有的标准关联容器类似,sets和multisets通常以平衡二叉树完成。
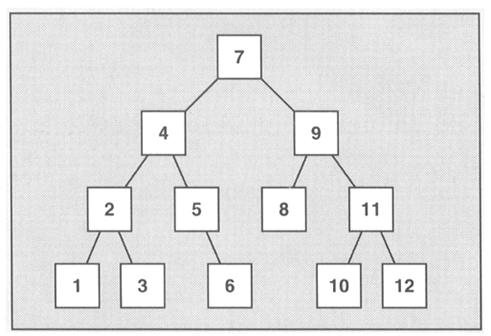
自动排序的主要优点在于使二叉树搜寻元素具有良好的性能,在其搜索函数算法具有对数复杂度。但是自动排序也造成了一个限制,不能直接改变元素值,因为这样会打乱原有的顺序,要改变元素的值,必须先删除旧元素,再插入新元素。所以sets和multisets具有以下特点:
- 不提供直接用来存取元素的任何操作元素
- 通过迭代器进行元素的存取。
3、操作函数
3.1 构造、拷贝、析构
|
操作 |
效果 |
|
set c |
产生一个空的set/multiset,不含任何元素 |
|
set c(op) |
以op为排序准则,产生一个空的set/multiset |
|
set c1(c2) |
产生某个set/multiset的副本,所有元素都被拷贝 |
|
set c(beg,end) |
以区间[beg,end)内的所有元素产生一个set/multiset |
|
set c(beg,end, op) |
以op为排序准则,区间[beg,end)内的元素产生一个set/multiset |
|
c.~set() |
销毁所有元素,释放内存 |
|
set<Elem> |
产生一个set,以(operator <)为排序准则 |
|
set<Elem,0p> |
产生一个set,以op为排序准则 |
3.2 非变动性操作
|
操作 |
效果 |
|
c.size() |
返回当前的元素数量 |
|
c.empty () |
判断大小是否为零,等同于0 == size(),效率更高 |
|
c.max_size() |
返回能容纳的元素最大数量 |
|
c1 == c2 |
判断c1是否等于c2 |
|
c1 != c2 |
判断c1是否不等于c2(等同于!(c1==c2)) |
|
c1 < c2 |
判断c1是否小于c2 |
|
c1 > c2 |
判断c1是否大于c2 |
|
c1 <= c2 |
判断c1是否小于等于c2(等同于!(c2<c1)) |
|
c1 >= c2 |
判断c1是否大于等于c2 (等同于!(c1<c2)) |
3.3 特殊的搜寻函数
sets和multisets在元素快速搜寻方面做了优化设计,提供了特殊的搜寻函数,所以应优先使用这些搜寻函数,可获得对数复杂度,而非STL的线性复杂度。比如在1000个元素搜寻,对数复杂度平均十次,而线性复杂度平均需要500次。
|
操作 |
效果 |
|
count (elem) |
返回元素值为elem的个数 |
|
find(elem) |
返回元素值为elem的第一个元素,如果没有返回end() |
|
lower _bound(elem) |
返回元素值为elem的第一个可安插位置,也就是元素值 >= elem的第一个元素位置 |
|
upper _bound (elem) |
返回元素值为elem的最后一个可安插位置,也就是元素值 > elem 的第一个元素位置 |
|
equal_range (elem) |
返回elem可安插的第一个位置和最后一个位置,也就是元素值==elem的区间 |
3.4 赋值
|
操作 |
效果 |
|
c1 = c2 |
将c2的元素全部给c1 |
|
c1.swap(c2) |
将c1和c2 的元素互换 |
|
swap(c1,c2) |
同上,全局函数 |
3.5 迭代器相关函数
sets和multisets的迭代器是双向迭代器,对迭代器操作而言,所有的元素都被视为常数,可以确保你不会人为改变元素值,从而打乱既定顺序,所以无法调用变动性算法,如remove()。
|
操作 |
效果 |
|
c.begin() |
返回一个随机存取迭代器,指向第一个元素 |
|
c.end() |
返回一个随机存取迭代器,指向最后一个元素的下一个位置 |
|
c.rbegin() |
返回一个逆向迭代器,指向逆向迭代的第一个元素 |
|
c.rend() |
返回一个逆向迭代器,指向逆向迭代的最后一个元素的下一个位置 |
3.6 安插和删除元素
必须保证参数有效,迭代器必须指向有效位置,序列起点不能位于终点之后,不能从空容器删除元素。
|
操作 |
效果 |
|
c.insert(elem) |
插入一个elem副本,返回新元素位置,无论插入成功与否。 |
|
c.insert(pos, elem) |
安插一个elem元素副本,返回新元素位置,pos为收索起点,提升插入速度。 |
|
c.insert(beg,end) |
将区间[beg,end)所有的元素安插到c,无返回值。 |
|
c.erase(elem) |
删除与elem相等的所有元素,返回被移除的元素个数。 |
|
c.erase(pos) |
移除迭代器pos所指位置元素,无返回值。 |
|
c.erase(beg,end) |
移除区间[beg,end)所有元素,无返回值。 |
|
c.clear() |
移除所有元素,将容器清空 |
4、示例代码
4.1 set
// cont/set1.cpp #include <iostream> #include <set> using namespace std; int main() { /*type of the collection: *-no duplicates *-elements are integral values *-descending order */ typedef set<int,greater<int> > IntSet; IntSet coll1; // empty set container //insert elements in random order coll1.insert(4); coll1.insert(3); coll1.insert(5); coll1.insert(1); coll1.insert(6); coll1.insert(2); coll1.insert(5); //iterate over all elements and print them IntSet::iterator pos; for (pos = coll1.begin(); pos != coll1.end(); ++pos) { cout << *pos << ' '; } cout << endl; //insert 4 again and process return value pair<IntSet::iterator,bool> status = coll1.insert(4); if (status.second) { cout << "4 inserted as element " << distance (coll1.begin(),status. first) + 1 << endl; } else { cout << "4 already exists" << endl; } //assign elements to another set with ascending order set<int> coll2(coll1.begin(), coll1.end()); //print all elements of the copy copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; //remove all elements up to element with value 3 coll2.erase (coll2.begin(), coll2.find(3)); //remove all elements with value 5 int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl; //print all elements copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; }
输出:
6 5 4 3 2 1 4 already exists 1 2 3 4 5 6 1 element(s) removed 3 4 6
4.2 multiset
// cont/mset1.cpp #include <iostream> #include <set> using namespace std; int main() { /*type of the collection: *-duplicates allowed *-elements are integral values *-descending order */ typedef multiset<int,greater<int> > IntSet; IntSet coll1, // empty multiset container //insert elements in random order coll1.insert(4); coll1.insert(3); coll1.insert(5); coll1.insert(l); coll1.insert(6); coll1.insert(2); coll1.insert(5); //iterate over all elements and print them IntSet::iterator pos; for (pos = coll1.begin(); pos != coll1.end(); ++pos) { cout << *pos << ' '; } cout << endl; //insert 4 again and process return value IntSet::iterator ipos = coll1.insert(4); cout << "4 inserted as element " << distance (coll1.begin(),ipos) + 1 << endl; //assign elements to another multiset with ascending order multiset<int> coll2(coll1.begin(), coll1.end()); //print all elements of the copy copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; //remove all elements up to element with value 3 coll2.erase (coll2.begin(), coll2.find(3)); //remove all elements with value 5 int num; num = coll2.erase (5); cout << num << " element(s) removed" << endl; //print all elements copy (coll2.begin(), coll2.end(), ostream_iterator<int>(cout," ")); cout << endl; }
输出:
6 5 5 4 3 2 1 4 inserted as element 5 1 2 3 4 4 5 5 6 2 element(s) removed 3 4 4 6