动态规划-1

Wiki解释

动态规划（英语：Dynamic programming，简称DP）是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。

动态规划常常适用于有重叠子问题^[1]和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。

通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

动态规划很有用处，尤其是在做算法题的时候？当然它也是最难的，虽然本质是分解问题，但是它是dynamic的。

0-1背包问题

比如现在背包里有5个物品，分别质量w为2，2，4，6，3

我们把每一层重复的状态（节点）合并，只记录不同的状态，然后基于上一层的状态集合，来推导下一层的状态集合。我们可以通过合并每一层重复的状态，这样就保证每一层不同状态的个数都不会超过 w 个（w 表示背包的承载重量），也就是例子中的 9。于是，我们就成功避免了每层状态个数的指数级增长。

我们用一个二维数组 states[n][w+1]，来记录每层可以达到的不同状态。

第 0 个（下标从 0 开始编号）物品的重量是 2，要么装入背包，要么不装入背包，决策完之后，会对应背包的两种状态，背包中物品的总重量是 0 或者 2。我们用 states[0][0]=true 和 states[0][2]=true 来表示这两种状态。

第 1 个物品的重量也是 2，基于之前的背包状态，在这个物品决策完之后，不同的状态有 3 个，背包中物品总重量分别是 0(0+0)，2(0+2 or 2+0)，4(2+2)。我们用 states[1][0]=true，states[1][2]=true，states[1][4]=true 来表示这三种状态。

以此类推，直到考察完所有的物品后，整个 states 状态数组就都计算好了。我把整个计算的过程画了出来，你可以看看。图中 0 表示 false，1 表示 true。我们只需要在最后一层，找一个值为 true 的最接近 w（这里是 9）的值，就是背包中物品总重量的最大值。

代码实现

    // weight:物品重量，n:物品个数，w:背包可承载重量
    public static int knapsack(int[] weight, int n, int w) {
        boolean[][] states = new boolean[n][w+1]; // 默认值false
        states[0][0] = true;  // 第一行的数据要特殊处理，可以利用哨兵优化
        if (weight[0] <= w) {
            states[0][weight[0]] = true;
        }
        for (int i = 1; i < n; ++i) { // 动态规划状态转移
            for (int j = 0; j <= w; ++j) {// 不把第i个物品放入背包
                if (states[i-1][j] == true) states[i][j] = states[i-1][j];
            }
            for (int j = 0; j <= w-weight[i]; ++j) {//把第i个物品放入背包
                if (states[i-1][j]==true) states[i][j+weight[i]] = true;
            }
        }
        for (int i = w; i >= 0; --i) { // 输出结果
            if (states[n-1][i] == true) return i;
        }
        return 0;
    }

看这段代码一定要确保上面的图示明白了。

实际上，这就是一种用动态规划解决问题的思路。我们把问题分解为多个阶段，每个阶段对应一个决策。我们记录每一个阶段可达的状态集合（去掉重复的），然后通过当前阶段的状态集合，来推导下一个阶段的状态集合，动态地往前推进。这也是动态规划这个名字的由来，你可以自己体会一下，是不是还挺形象的？

尽管动态规划的执行效率比较高，但是就刚刚的代码实现来说，我们需要额外申请一个 n 乘以 w+1 的二维数组，对空间的消耗比较多。所以，有时候，我们会说，动态规划是一种空间换时间的解决思路。你可能要问了，有什么办法可以降低空间消耗吗？

0-1背包升级

我们刚刚讲的背包问题，只涉及背包重量和物品重量。我们现在引入物品价值这一变量。对于一组不同重量、不同价值、不可分割的物品，我们选择将某些物品装入背包，在满足背包最大重量限制的前提下，背包中可装入物品的总价值最大是多少呢？

这个问题依旧可以用回溯算法来解决。这个问题并不复杂，所以具体的实现思路，我就不用文字描述了，直接给你看代码。

private int maxV = Integer.MIN_VALUE; // 结果放到maxV中
private int[] items = {2，2，4，6，3};  // 物品的重量
private int[] value = {3，4，8，9，6}; // 物品的价值
private int n = 5; // 物品个数
private int w = 9; // 背包承受的最大重量
public void f(int i, int cw, int cv) { // 调用f(0, 0, 0)
  if (cw == w || i == n) { // cw==w表示装满了，i==n表示物品都考察完了
    if (cv > maxV) maxV = cv;
    return;
  }
  f(i+1, cw, cv); // 选择不装第i个物品
  if (cw + weight[i] <= w) {
    f(i+1,cw+weight[i], cv+value[i]); // 选择装第i个物品
  }
}

针对上面的代码，我们还是照例画出递归树。在递归树中，每个节点表示一个状态。现在我们需要 3 个变量（i, cw, cv）来表示一个状态。其中，i 表示即将要决策第 i 个物品是否装入背包，cw 表示当前背包中物品的总重量，cv 表示当前背包中物品的总价值。

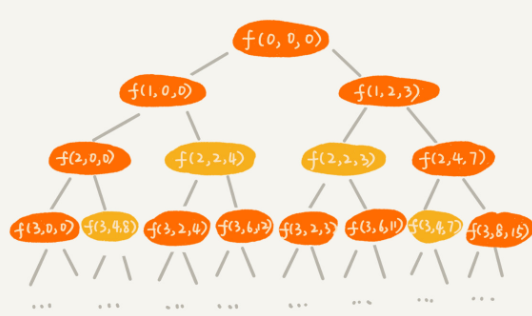
我们还是把整个求解过程分为 n 个阶段，每个阶段会决策一个物品是否放到背包中。每个阶段决策完之后，背包中的物品的总重量以及总价值，会有多种情况，也就是会达到多种不同的状态。

我们用一个二维数组 states[n][w+1]，来记录每层可以达到的不同状态。不过这里数组存储的值不再是 boolean 类型的了，而是当前状态对应的最大总价值。我们把每一层中 (i, cw) 重复的状态（节点）合并，只记录 cv 值最大的那个状态，然后基于这些状态来推导下一层的状态。

public static int knapsack3(int[] weight, int[] value, int n, int w) {
  int[][] states = new int[n][w+1];
  for (int i = 0; i < n; ++i) { // 初始化states
    for (int j = 0; j < w+1; ++j) {
      states[i][j] = -1;
    }
  }
  states[0][0] = 0;
  if (weight[0] <= w) {
    states[0][weight[0]] = value[0];
  }
  for (int i = 1; i < n; ++i) { //动态规划，状态转移
    for (int j = 0; j <= w; ++j) { // 不选择第i个物品
      if (states[i-1][j] >= 0) states[i][j] = states[i-1][j];
    }
    for (int j = 0; j <= w-weight[i]; ++j) { // 选择第i个物品
      if (states[i-1][j] >= 0) {
        int v = states[i-1][j] + value[i];
        if (v > states[i][j+weight[i]]) {
          states[i][j+weight[i]] = v;
        }
      }
    }
  }
  // 找出最大值
  int maxvalue = -1;
  for (int j = 0; j <= w; ++j) {
    if (states[n-1][j] > maxvalue) maxvalue = states[n-1][j];
  }
  return maxvalue;
}

双十一拼单问题

 实际上，它跟第一个例子中讲的 0-1 背包问题很像，只不过是把“重量”换成了“价格”而已。购物车中有 n 个商品。我们针对每个商品都决策是否购买。每次决策之后，对应不同的状态集合。我们还是用一个二维数组 states[n][x]，来记录每次决策之后所有可达的状态。不过，这里的 x 值是多少呢？

0-1 背包问题中，我们找的是小于等于 w 的最大值，x 就是背包的最大承载重量 w+1。对于这个问题来说，我们要找的是大于等于 200（满减条件）的值中最小的，所以就不能设置为 200 加 1 了。就这个实际的问题而言，如果要购买的物品的总价格超过 200 太多，比如 1000，那这个羊毛“薅”得就没有太大意义了。所以，我们可以限定 x 值为 1001。

不过，这个问题不仅要求大于等于 200 的总价格中的最小的，我们还要找出这个最小总价格对应都要购买哪些商品。实际上，我们可以利用 states 数组，倒推出这个被选择的商品序列。

// items商品价格，n商品个数, w表示满减条件，比如200
public static void double11advance(int[] items, int n, int w) {
  boolean[][] states = new boolean[n][3*w+1];//超过3倍就没有薅羊毛的价值了
  states[0][0] = true;  // 第一行的数据要特殊处理
  if (items[0] <= 3*w) {
    states[0][items[0]] = true;
  }
  for (int i = 1; i < n; ++i) { // 动态规划
    for (int j = 0; j <= 3*w; ++j) {// 不购买第i个商品
      if (states[i-1][j] == true) states[i][j] = states[i-1][j];
    }
    for (int j = 0; j <= 3*w-items[i]; ++j) {//购买第i个商品
      if (states[i-1][j]==true) states[i][j+items[i]] = true;
    }
  }

  int j;
  for (j = w; j < 3*w+1; ++j) { 
    if (states[n-1][j] == true) break; // 输出结果大于等于w的最小值
  }
  if (j == 3*w+1) return; // 没有可行解
  for (int i = n-1; i >= 1; --i) { // i表示二维数组中的行，j表示列
    if(j-items[i] >= 0 && states[i-1][j-items[i]] == true) {
      System.out.print(items[i] + " "); // 购买这个商品
      j = j - items[i];
    } // else 没有购买这个商品，j不变。
  }
  if (j != 0) System.out.print(items[0]);
}

（入门）

参考王争老师《数据结构与算法》