排序-1

选择排序

遍历找最小，依次放左端。

一种最简单的排序算法是这样的：首先，找到数组中最小的那个元素，其次，将它和数组的第 一个元素交换位置（如果第一个元素就是最小元素那么它就和自己交换）。再次，在剩下的元素中 找到最小的元素，将它与数组的第二个元素交换位置。如此往复，直到将整个数组排序。这种方法 叫做选择排序，因为它在不断地选择剩余元素之中的最小者。

模板方法

    public static void sort(){}
    public static boolean less(int a, int b){}
    public static void exch(int[] a, int i, int j){}
    public static boolean isSorted(int[] a) {
        for (int i = 0; i < a.length; i++) {
            if (less(a[i], a[i - 1])) {
                return false;
            } else {
                return true;
            }
        }
    }

 排序算法

    public static seletSort(int[] a) {
        int n = a.length;
        for (int i = 0; i < n; i++) {
            int min = i;
            for (int j = i + 1; j < n; j++) {
                if (less(a[j], a[min])) {
                    min = j;
                }
            }
            exch(a, i, min);
        }
    }

插入排序

与选择排序一样，当前索引左边的所有元素都是有序的，但它们的最终位置还不确定，为了给 更小的元素腾出空间，它们可能会被移动。但是当索引到达数组的右端时，数组排序就完成了。 和选择排序不同的是，插入排序所需的时间取决于输入中元素的初始顺序。例如，对一个很大且其中的元素已经有序（或接近有序）的数组进行排序将会比对随机顺序的数组或是逆序数组进行排序要快得多。

‰ 数组中每个元素距离它的最终位置都不远；

‰ 一个有序的大数组接一个小数组；

‰ 数组中只有几个元素的位置不正确。

插入排序对这样的数组很有效，而选择排序则不然。事实上，当倒置的数量很少时，插入排序 很可能比本章中的其他任何算法都要快。

    public static void insertSort(int[] a) {
        int n = a.length;
        for (int i = 1; i < n; i++) {
            for (int j = i; j > 0 && less(a[j], a[j - 1]); j--) {
                exch(a, j, j - 1);
            }
        }
    }

希尔排序

https://www.cnblogs.com/chengxiao/p/6104371.html这篇讲的不错

    public static void shellSort(int[] a) {
        for (int gap = a.length / 2; gap > 0; gap /= 2) {
            for (int i = gap; i < a.length; i++) {
                int j = i;
                while (j - gap >= 0 && a[j] < a[j - gap]) {
                    exch(a, j, j - gap);
                    j -= gap;
                }
            }
        }
    }

和选择排序以及插入排序形成对比的是，希尔排序也可以用于大型数组。它对任意排序（不一定 是随机的）的数组表现也很好。

有经验的程序员有时会选择希尔排序，因为对于中等大小的数组它的运行时间是可以接受的。 它的代码量很小，且不需要使用额外的内存空间。在下面的几节中我们会看到更加高效的算法，但 除了对于很大的N，它们可能只会比希尔排序快两倍（可能还达不到），而且更复杂。如果你需要 解决一个排序问题而又没有系统排序函数可用（例如直接接触硬件或是运行于嵌入式系统中的代 码），可以先用希尔排序，然后再考虑是否值得将它替换为更加复杂的排序算法。

归并排序

原地归并排序--抽象方法

   public static void merge(int[] a, int lo, int mid, int hi) {
        int i = lo;
        int j = mid + 1;
        int[] aux = new int[a.length];
        for (int k = 0; k < a.length; k++) {
            aux[k] = a[k];
        }
        for (int k = lo; k < hi; k++) {
            if (j == hi) {
                a[k] = aux[i++];
            }
            if (i > mid) {
                a[k] = aux[j++];
            }
            if (less(aux[j], aux[i])) {
                a[k] = aux[j++];
            } else {
                a[k] = aux[i++];
            }
        }
    }

自顶向下的归并排序-分治，递归

 public static void sort(int[] a) {
        aux = new int[a.length];
        sort(a, 0, a.length - 1);
    }
    public static void sort(int[] a, int lo, int hi) {
        if (hi <= lo) {
            return;
        }
        int mid = lo + (hi - lo) / 2;
        sort(a, lo, mid);
        sort(a, mid + 1, hi);
        merge(a, lo, mid, hi);
    }

自底向上的归并排序

    public static void deepToUpSort(int[] a) {
        int n = a.length;
        aux = new int[n];
        for (int sz = 1; sz < n; sz += sz) {
            for (int lo = 0; lo < n - sz; lo += 2 * sz) {
                merge(a, lo, lo + sz - 1, Math.min(n - 1, lo + 2 * sz - 1));
            }
        }
    }

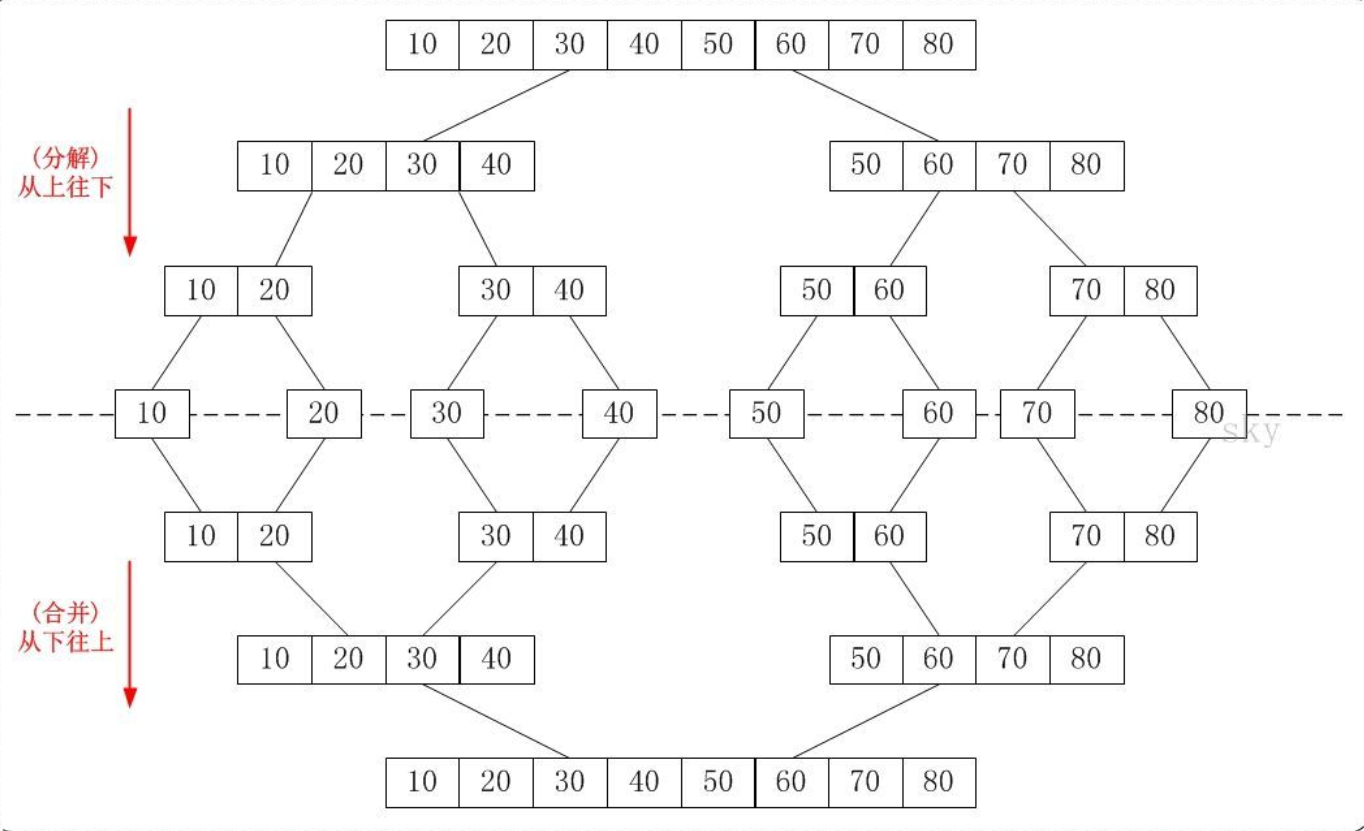
归并排序的空间复杂度不是最优的