Python习题之快乐的数字

快乐的数字

描述

　　编写一个算法来确定一个数字是否“快乐”。 快乐的数字按照如下方式确定：从一个正整数开始，用其每位数的平方之和取代该数，并重复这个过程，直到最后数字要么收敛等于1且一直等于1，要么将无休止地循环下去且最终不会收敛等于1。能够最终收敛等于1的数就是快乐的数字。‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬

　　例如: 19 就是一个快乐的数字，计算过程如下：‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‮‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‭‬‫‬‪‬‪‬‪‬‪‬‪‬‮‬‪‬‭‬

• 1² + 9² = 82
• 8² + 2² = 68
• 6² + 8² = 100
• 1² + 0² + 0² = 1

　　当输入时快乐的数字时，输出True，否则输出False。 

示例

　　输入：19   输出：True

题干分析

　　首先，我们需要得到一个数字，判断它是几位数，然后分别取它的每一位数，平方再相加，如此循环下去，直到最后结果为1，输出True，否则，输出False。

　　那么，如果一个数字不是快乐数，它会不会无限循环下去呢？我们可以找几个数字来试一试。

　　2：2**2=4；4**2=16；1**2+6**2=37；3**2+7**2=58；5**2+8**2=89；8**2+9**2=145；1**2+4**2+5**2=42；4**2+2**2=20；2**2+0**2=4......

　　21：2**2+1**2=5；5**2=25；2**2+5**2=29；2**2+9**2=85；8**2+5**2=89；8**2+9**2=145；1**2+4**2+5**2=42；4**2+2**2=20；2**2+0**2=4......

　　35：3**2+5**2=34；3**2+4**2=25；5**2=25；2**2+5**2=29；2**2+9**2=85；8**2+5**2=89；8**2+9**2=145；1**2+4**2+5**2=42；4**2+2**2=20；2**2+0**2=4......

　　57：5**2+7**2=74；7**2+4**2=65；6**2+5**2=61；6**2+1**2=37；3**2+7**2=58；5**2+8**2=89；8**2+9**2=145；1**2+4**2+5**2=42；4**2+2**2=20；2**2+0**2=4......

　　123：1**2+2**2+3**2=14；1**2+4**2=17；1**2+7**2=50；5**2+0**2=25；2**2+5**2=29；2**2+9**2=85；8**2+5**2=89；8**2+9**2=145；1**2+4**2+5**2=42；4**2+2**2=20；2**2+0**2=4......

　　91：9**2+1**2=82；8**2+2**2=68；6**2+8**2=100；1**2+0**2+0**2=1

　　由此，我们可以看出，如果是快乐数，那么最后计算的值为1；而不是快乐数，最后计算的结果一定有4。因此可以限定循环的判断条件为1和4，即当和为1或4时跳出循环，以此来防止无限循环。

代码及运行结果展示

　　函数方法

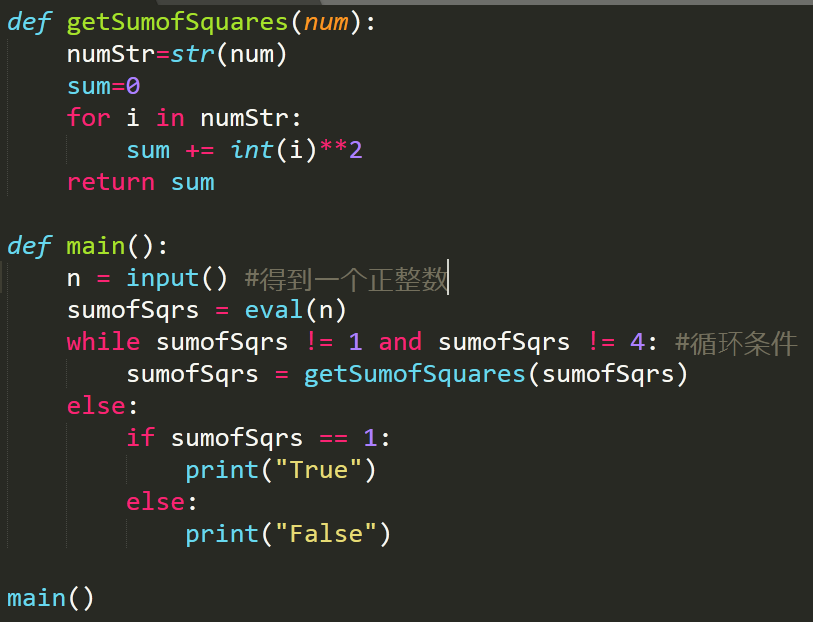
 　　运行结果

 

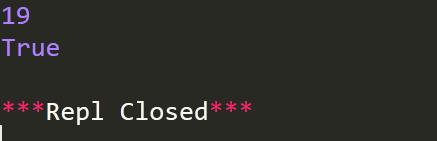
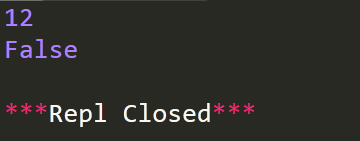
 　　异常处理方法

 　 运行结果

 

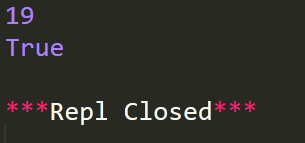
　　这是我目前想到的两种方法，如果大家还有别的方法，欢迎跟我一起探讨！

　

---