You are given two arrays A and B, each of size n. The error, E, between these two arrays is defined 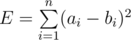 . You have to perform exactly k1 operations on array A and exactly k2 operations on array B. In one operation, you have to choose one element of the array and increase or decrease it by 1.
. You have to perform exactly k1 operations on array A and exactly k2 operations on array B. In one operation, you have to choose one element of the array and increase or decrease it by 1.
Output the minimum possible value of error after k1 operations on array A and k2 operations on array B have been performed.
The first line contains three space-separated integers n (1 ≤ n ≤ 103), k1 and k2 (0 ≤ k1 + k2 ≤ 103, k1 and k2 are non-negative) — size of arrays and number of operations to perform on A and B respectively.
Second line contains n space separated integers a1, a2, ..., an ( - 106 ≤ ai ≤ 106) — array A.
Third line contains n space separated integers b1, b2, ..., bn ( - 106 ≤ bi ≤ 106)— array B.
Output a single integer — the minimum possible value of 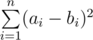 after doing exactly k1 operations on array A and exactly k2 operations on array B.
after doing exactly k1 operations on array A and exactly k2 operations on array B.
2 0 0
1 2
2 3
2
2 1 0
1 2
2 2
0
2 5 7
3 4
14 4
1
In the first sample case, we cannot perform any operations on A or B. Therefore the minimum possible error E = (1 - 2)2 + (2 - 3)2 = 2.
In the second sample case, we are required to perform exactly one operation on A. In order to minimize error, we increment the first element of A by 1. Now, A = [2, 2]. The error is now E = (2 - 2)2 + (2 - 2)2 = 0. This is the minimum possible error obtainable.
In the third sample case, we can increase the first element of A to 8, using the all of the 5 moves available to us. Also, the first element of B can be reduced to 8 using the 6 of the 7 available moves. Now A = [8, 4] and B = [8, 4]. The error is now E = (8 - 8)2 + (4 - 4)2 = 0, but we are still left with 1 move for array B. Increasing the second element of B to 5 using the left move, we get B = [8, 5] and E = (8 - 8)2 + (4 - 5)2 = 1.
分析题目,不难发现,每一次对Ai进行操作,等价于对Bi进行一次相反的操作。因此我们可以认为操作数K1与K2是等价的,我们大可合并成一个总的操作数Sum=K1+K2看代。
同时因为Ai与Bi存在着一一对应的关系,再加上最终所求也只与Ai,Bi的差值有关,故可以从最开始将Ai、Bi看成一个整体,直接存储Ai与Bi的差的绝对值Ci,这样就相对简化了讨论。
于是,题目就转化成:在进行Sum次+1或-1的操作下,要使得∑(i=1->n)Ci^2最小即可
因为我们要Ci^2最小,因此每次操作数都必须要取Ci中的最大值进行操作。而维护一堆数中的最大值,最方便的操作就是用STL中的优先队列(当然每次都进行一次sort也可以)
操作完之后只需要简单的统计答案即可。
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define maxn 1000005
int a[maxn];
int b[maxn];
int num[maxn];
priority_queue<ll>que;
int main(){
int n,k1,k2;
cin>>n>>k1>>k2;//读入n和k1,k2
for(int i=1;i<=n;i++){
cin>>a[i];//读入数组a的大小
}
for(int i=1;i<=n;i++){
cin>>b[i];//读入数组b的大小
que.push(abs(a[i]-b[i]));//将a[i]与b[i]的差的绝对值进入优先队列
}
int sum=k1+k2;//统计总共的操作数
while(sum>0){//如果操作数大于0
ll tmp=que.top();//取队顶元素
que.pop();//剔除队顶元素
que.push(abs(tmp-1));//将所取的队顶元素-1同时将所求结果的绝对值压入优先队列中
sum--;//操作数-1
}
ll res=0;
while(!que.empty()){//考虑进行完操作后的情况
ll tmp=que.top();//取队顶元素
que.pop();
res+=1ll*tmp*tmp;//统计答案
}
cout<<res<<endl;
return 0;
}