传送门
题面:
F. Multicolored Markers
time limit per test
3 seconds
memory limit per test
256 megabytes
input
standard input
output
standard output
There is an infinite board of square tiles. Initially all tiles are white.
Vova has a red marker and a blue marker. Red marker can color aa tiles. Blue marker can color bb tiles. If some tile isn't white then you can't use marker of any color on it. Each marker must be drained completely, so at the end there should be exactly aa red tiles and exactly bb blue tiles across the board.
Vova wants to color such a set of tiles that:
- they would form a rectangle, consisting of exactly a+ba+b colored tiles;
- all tiles of at least one color would also form a rectangle.
Here are some examples of correct colorings:
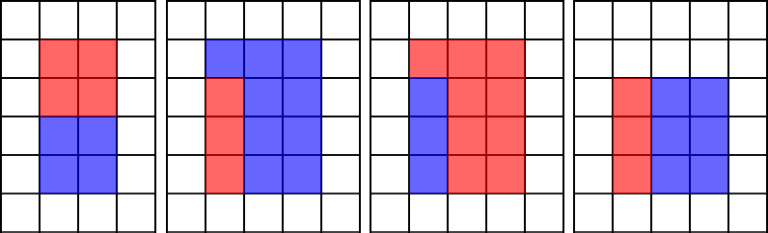
Here are some examples of incorrect colorings:
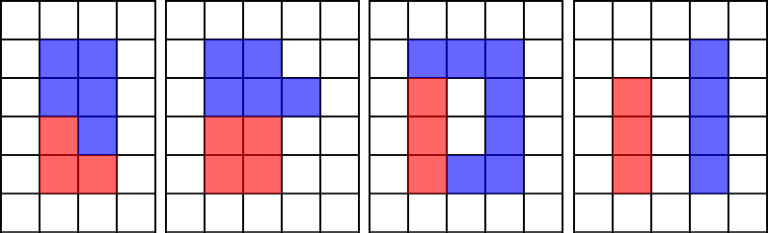
Among all correct colorings Vova wants to choose the one with the minimal perimeter. What is the minimal perimeter Vova can obtain?
It is guaranteed that there exists at least one correct coloring.
Input
A single line contains two integers aa and bb (1≤a,b≤10141≤a,b≤1014) — the number of tiles red marker should color and the number of tiles blue marker should color, respectively.
Output
Print a single integer — the minimal perimeter of a colored rectangle Vova can obtain by coloring exactly aa tiles red and exactly bb tiles blue.
It is guaranteed that there exists at least one correct coloring.
Examples
input
Copy
4 4
output
Copy
12
input
Copy
3 9
output
Copy
14
input
Copy
9 3
output
Copy
14
input
Copy
3 6
output
Copy
12
input
Copy
506 2708
output
Copy
3218
Note
The first four examples correspond to the first picture of the statement.
Note that for there exist multiple correct colorings for all of the examples.
In the first example you can also make a rectangle with sides 11 and 88, though its perimeter will be 1818 which is greater than 88.
In the second example you can make the same resulting rectangle with sides 33 and 44, but red tiles will form the rectangle with sides 11 and 33 and blue tiles will form the rectangle with sides 33 and 33.
题意:
有a个红瓷砖,b个蓝瓷砖,要使得这些瓷砖组成一个完整的矩形,同时要保证a个红瓷砖或b个蓝瓷砖能够组成一个完整的矩阵,问你能够构成的这么多方案数中,构造出的完整的矩形的最小的周长为多少。
题目分析:
这是一个挺有意思的思维。
首先,依题意不难发现,红瓷砖的面积和为a,蓝瓷转的面积和为b,总矩阵的面积和为a+b。
因此,此时面积为已知条件,让我们求周长。我们可以想到貌似可以枚举红瓷砖和蓝瓷转的边长去处理这个问题。
同时,因为题目要求红蓝瓷砖必定有一种是可以构成矩形的,总矩阵必定是能构成矩阵的,因此我们在枚举它们的一条边长i的过程中,还需要对判断由该边长i是否能够构成一个面积为a/b/a+b的矩阵(判断面积是否能整除i)。
而对于那些合法的边长,因为我们要求的是要构造出边长尽可能小的矩阵,因此我们可以用可以set去维护所有合法的边长即可。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
set<ll>st;
int main()
{
ll a,b;
cin>>a>>b;
ll n=(a+b);//总面积
ll res=1e18;
for(ll i=1;i*i<=n;i++){//枚举边长
if(a%i==0) st.insert(a/i);//如果红色瓷砖能够构成矩阵,存边长
if(b%i==0) st.insert(b/i);//如果蓝色瓷砖能够构成矩阵,存边长
if(n%i==0){//如果总面积能够构成矩阵,则判断之前是否存在合法的红蓝瓷砖,进而更新答案
ll h=i;
ll w=n/i;
if(*st.begin()<=w){
res=min(res,h*2+w*2);
}
}
}
cout<<res<<endl;
}