本文提到的「B-树」,就是「B树」,都是 B-tree 的翻译,里面不是减号-,是连接符-。因为有人把 B-tree 翻成 「B-树」,让人以为「B树」和「B-树」是两种树,实际上两者就是同一种树。
Mysql数据库里面的索引是基于什么数据结构了呢?
主要是基于Hash表或者B+树。
B+树的具体实现细节?B-树和B+树有什么区别呢?联合索引在B+树中如何存储呢?
要知道这些,我们需要先了解什么是B-树。数据库索引之所以要使用树结构存储,是因为树的查询效率高,而且可以保持有序。为什么索引不使用二叉查找来树来实现呢?(///二叉查找树查询的时间复杂读是0(logN),性能已经足够高了啊,难道B树可以比它更快?)其实从算法逻辑上讲,二叉查找树的查找速度和比较次数都是最小的,但是为我们不得不考虑一个现实的问题:磁盘 IO。
数据库索引是存储在磁盘上的,当数据量比较打的时候,索引的大小可能有几个G甚至更多。当我们利用索引查询的时候,能把整个索引全部加载到内存吗?不可能,能做的只有逐一的加载每一个磁盘页对应着索引树的节点。

如果我们利用二叉查找树作为索引结构,情形是什么呢?假设树的高度是4,查找的值是10,流程如下:
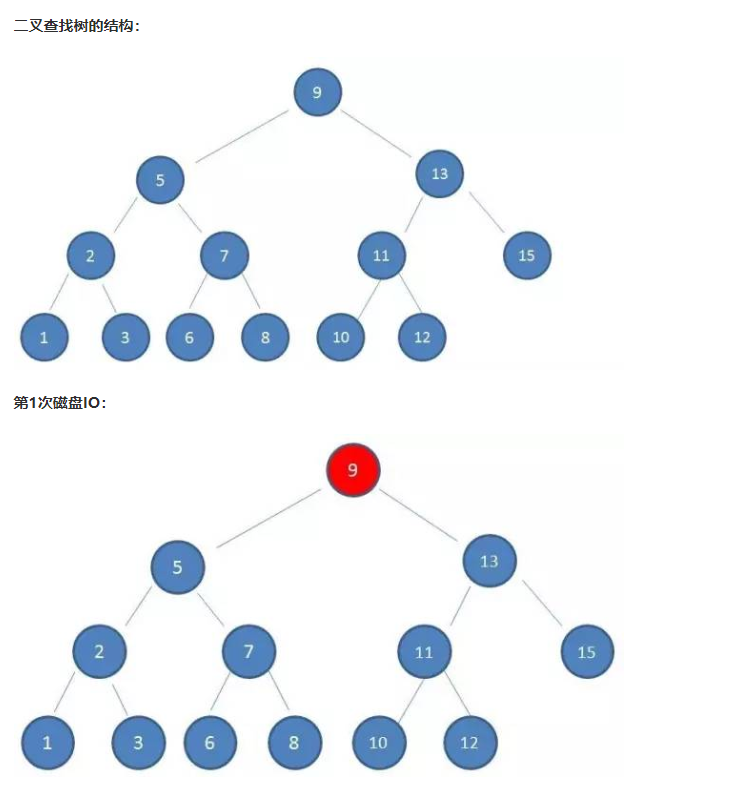


由上可以看出,磁盘IO的次数是由索引树高度决定,所以为了减少磁盘IO次数,我们需要减少树的高度,这就是B-树的特征之一。
B树的定义:
两种定义:用阶定义的B树 & 用阶定义的B树
用阶定义的B树 :
B 树又叫平衡多路查找树。一棵m阶的B 树 (注:切勿简单的认为一棵m阶的B树是m叉树,虽然存在四叉树,八叉树,KD树,及vp/R树/R*树/R+树/X树/M树/线段树/希尔伯特R树/优先R树等空间划分树,但与B树完全不等同)的特性如下:
- 树中每个结点最多含有m个孩子(m>=2);
- 除根结点和叶子结点外,其它每个结点至少有[ceil(m / 2)]个孩子(其中ceil(x)是一个取上限的函数);
- 若根结点不是叶子结点,则至少有2个孩子(特殊情况:没有孩子的根结点,即根结点为叶子结点,整棵树只有一个根节点);
- 所有叶子结点都出现在同一层,叶子结点不包含任何关键字信息(其实,关键是把什么当做叶子结点,因为如红黑树中,每一个NULL指针即当做叶子结点,只是没画出来而已)。
- 每个非终端结点中包含有n个关键字信息: (n,P0,K1,P1,K2,P2,......,Kn,Pn)。其中:
a) Ki (i=1...n)为关键字,且关键字按顺序升序排序K(i-1)< Ki。
b) Pi为指向子树根的接点,且指针P(i-1)指向子树种所有结点的关键字均小于Ki,但都大于K(i-1)。
c) 关键字的个数n必须满足: [ceil(m / 2)-1]<= n <= m-1。如下图所示:

用度定义的B树:
针对上面的5点,再阐述下:B树中每一个结点能包含的关键字(如之前上面的D H和Q T X)数有一个上界和下界。这个下界可以用一个称作B树的最小度数(算法导论中文版上译作度数,最小度数即内节点中节点最小孩子数目)m(m>=2)表示。
每个非根的内结点至多有m个子女,每个非根的结点必须至少含有m-1个关键字,如果树是非空的,则根结点至少包含一个关键字;
每个结点可包含至多2m-1个关键字。所以一个内结点至多可有2m个子女。如果一个结点恰好有2m-1个关键字,我们就说这个结点是满的(而稍后介绍的B*树作为B树的一种常用变形,B*树中要求每个内结点至少为2/3满,而不是像这里的B树所要求的至少半满);
当关键字数m=2(t=2的意思是,mmin=2,m可以>=2)时的B树是最简单的(有很多人会因此误认为B树就是二叉查找树,但二叉查找树就是二叉查找树,B树就是B树,B树是一棵含有m(m>=2)个关键字的平衡多路查找树),此时,每个内结点可能因此而含有2个、3个或4个子女,亦即一棵2-3-4树,然而在实际中,通常采用大得多的t值。
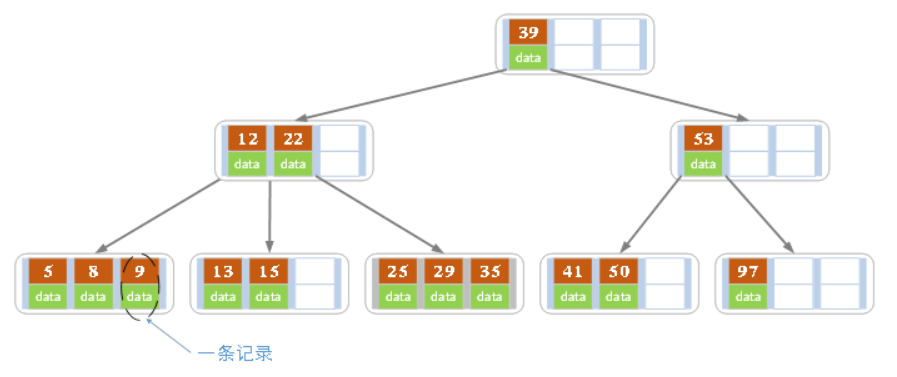
上图是一颗阶数为4的B树。在实际应用中的B树的阶数m都非常大(通常大于100),所以即使存储大量的数据,B树的高度仍然比较小。每个结点中存储了关键字(key)和关键字对应的数据(data),以及孩子结点的指针。我们将一个key和其对应的data称为一个记录。
B-树的查询:
演示如下:假设查询5

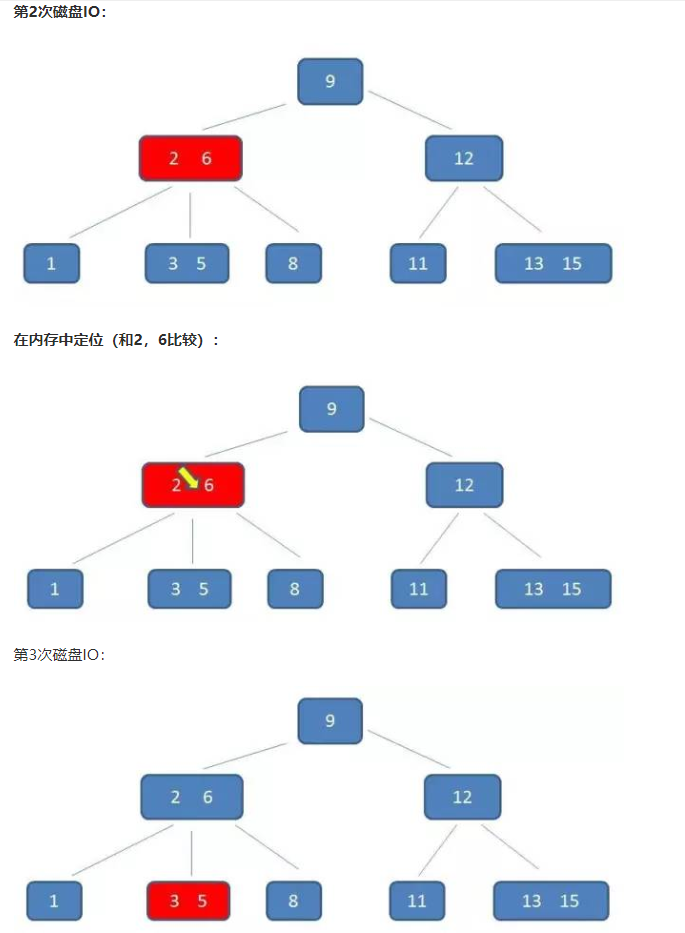
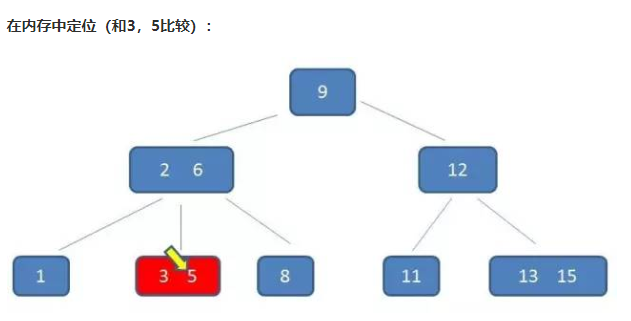

插入:
B-树的插入过程比较复杂,我们只举一个最金典的例子,插入4

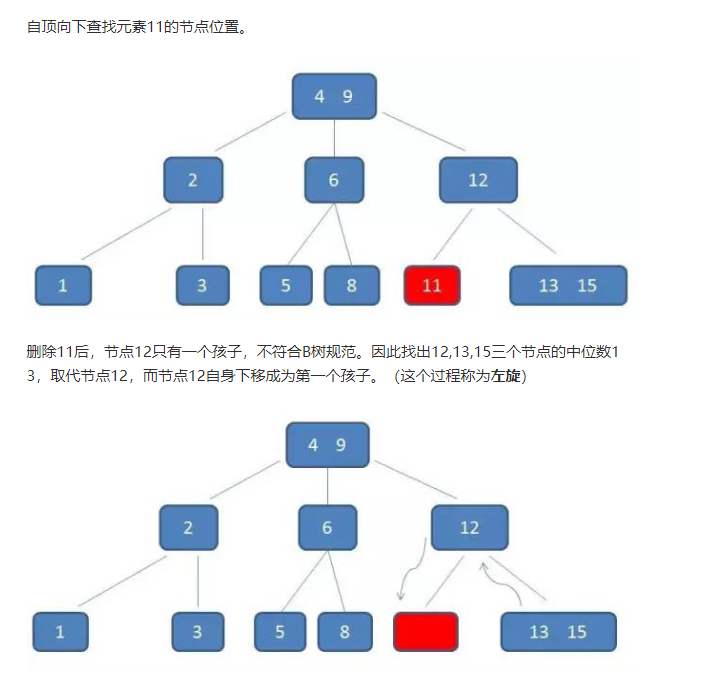
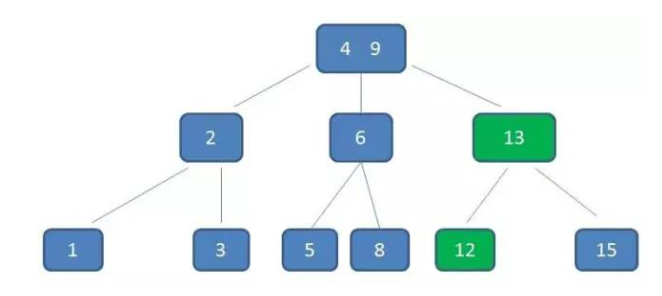
删除:11