既然是详解, 就从最基础的讲起了.
1. Bit(位)
Bit计算机是计算机最小的存储单位, 大家都知道计算机实质上都是用二进制数0或者1来存储数据的, 所以Bit实际上可以看成存放1个二进制数字的1个位置.
也就是说bit只有2种值, 0 或者 1, 所以1个bit能存放1个布尔类型的值(boolean,是或者否).
如果一个布尔类型被存放在1个bit中, 自然这个变量就占用1个bit了, 无论这个值是1或者0, 它都占用1个bit...
2. Byte(字节)
这个就厉害了, 因为我们平常讲的1个文件占多少KB, MB... 1个硬盘占多少GB.. 等后面的这个B, 指的就是字节Byte, 而不是上面的Bit, 而且1个Byte = 8Bit, 这个怎么理解呢?
其实1个Byte 可以看成是有8个物理上连续的Bit组成的, 如下图:

上面说了, 1个Bit 只能表示两种值0 or 1, 其实就是2^1(2的1次方)种值啦.
那么1个Byte能表示多少种值呢, 很简单就是2^8 = 256种啦
逻辑上就是因为1个Byte 是由8个bit组成的, 每1个bit可以有两种值(0 or 1), 那么8个bit根据概率组合论就有2^8 = 256种了.
它们分别是:
二进制: 0000 0000 0000 0001 0000 0010 0000 0011 ... 0000 1111 0001 0000 ... 1111 1111
十进制: 0 1 2 3 ... 15 16 ... 255
十六进制: 0 0 1 2 3 ... 0 F 1 0 ... F F
可以看出如下几点:
a. 这256个值分别是0~255 所以1个字节能表示最大的值就是255, 所以很多时候我们见到有255最大的限制(例如ip地址)就是这个原因啊。
b. 二进制1个字节是由8个位组成的,而每4个位可以看成1组,由1个十六进制数字来表示。也就是说十六进制的0-F分别表示二进制的0000 - 1111, 所以用16进制和2进制的转化其实是很方便的。
3. 内存是计算机系统的主存储器
介绍上面两个存储单位后就介绍下内存了。
内存作为1个存储数据的存在,有1个很重要的特性,就是内存里的数据能被cpu直接访问。
cpu能不能直接访问硬盘的数据呢,不能。只能通过把硬盘的数据先放到内存里,然后再从内存里访问硬盘的数据。我们平时玩游戏碰上读图loading 进度条的这个过程,就是把数据从硬盘读到内存的过程啊。读完条后地图的数据就在内存中了。
所以内存才是计算机系统的主存储器,而硬盘是被分到跟光盘..u盘一类都是外部存储器。
4. 内存的基本结构
内存里存放的数据是什么呢?其实也是只是存放0或者1这两个二进制数字啊,所以内存里实际上有海量的小格子,每1个格子是1个bit,就只能存放1个数字(0或者1),那么数值255需要几个格子来放呢?就是8个格子啊, 1个字节byte啊。
但是问题来了,我刚说了内存里的格子数量非常巨大,如果cpu要读出某个指定的数据,怎么去找呢?
1个1个格子去遍历吗,其实稍微接触过数据结构的都知道,遍历虽然实现简单,但是在海量数据面前简直是自杀行为。
所以实际上内存是把8个8个bit排成1组,每1组成为1个单位,大小是1byte(字节), cpu每一次只能访问1个byte,而不能单独去访问具体的1个小格子(bit). 1个byte字节就是内存的最小的IO单位.
也就是说内存是由8个 8个小格(bit)组成的1个字节单位(byte)排列组成的。如下图:
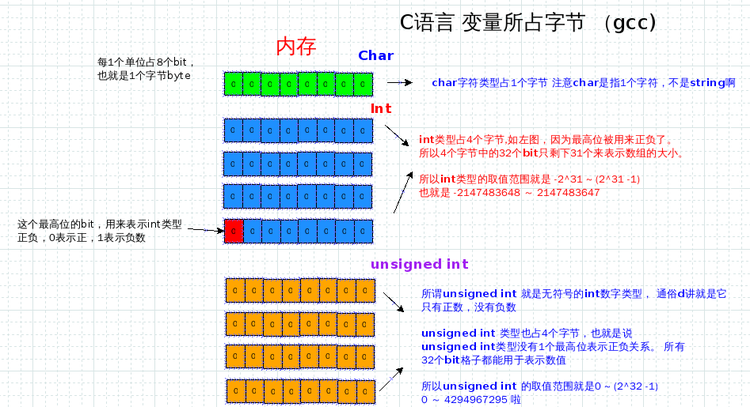
其实大部分数据都会作为各种数据类型存放在内存内,而各种数据类型所占的字节大小也是不同的,例如上图解析的,char字符类型占1个字节, int类型和unsigned int类型占4个字节byte.
5. 引入内存地址概念。
即使我们把内存分成了以字节为单位的结构,但是实际上内存里还是有非常多的字节的,例如64MB内存就有 64 × 1024 × 1024 个字节啊!
如果cpu要查找1个变量,还是要1个个字节去找到话...还是1个很浪费时间的行为,所以为了避免去遍历内存,计算机系统就引入了内存地址这个概念。
举个例子, 内存就是一栋大楼, 而内存里每1个字节就是大楼的每个房间, 而内存地址就是房间的门牌号码了. 如果没有门牌号码,我们去访问某个住在大楼的人是十分苦难的, 只能从1楼开始每个房间去敲门.. 如果那个人住在顶楼你就悲剧了. 而如果你知道那个人的门牌号码, 就可以直接上去敲他的门查他水表了, 实在是方便很多啊.
内存也一样, 计算机操作系统会给内存每1个字节分配1个内存地址, cpu只需要知道某个数据类型的地址, 就可以直接去到读影的内存位置去提取数据了.
6. 直接寻址技术.
当代计算机还实现了1个逆天的技术,就是直接寻址了.
什么意思呢, 还是用上面的例子说明, 假如你知道你要找的人住在那栋大楼的17楼 1702, 但是你还是需要从1楼走到17楼去找他, 这个过程还是需要时间成本的.
但是如果你具有了直接寻址技术, 就能直接跳到17楼 1702门前, 如果你找的下1个人在2楼, 又能从17楼直接跳到2楼, 逆天啊.
而直接寻址技术已经成为当代计算机软硬件的标准技术之一了, 也就是说只要cpu知道要访问数据的内存地址, 就能直接到内存的对应位置去访问数据!
7. 内存地址的表示方式
跟门牌号一样, 其实内存地址也是由1个2进制数字来表示的. 每1个地址对应内存里的1个byte字节, 如果地址的值加1, 那么这个地址就对应下1个字节了.
那么内存地址的长度是多少呢? 这个就是这篇文章标题所涉及的. 在32位操作系统中, 内存的地址就是32位的2进制数, 那么假如32位系统的某个内存地址是:
0000 1111 1111 0000 1111 0000 1111 0000
那么它可以用十六进制表示成: 0 F F 0 F 0 F 0
也就是
Ox0ff0f0f0 前面Ox代表十六进制, 所以你见到这种字母数字混合一次的地址方式,就是这样得来的了, 它实际上是1个二进制的数字啊. 不过计算机里面所有的东西都是二进制了..
8. 内存地址的数量决定cpu能访问的内存大小.
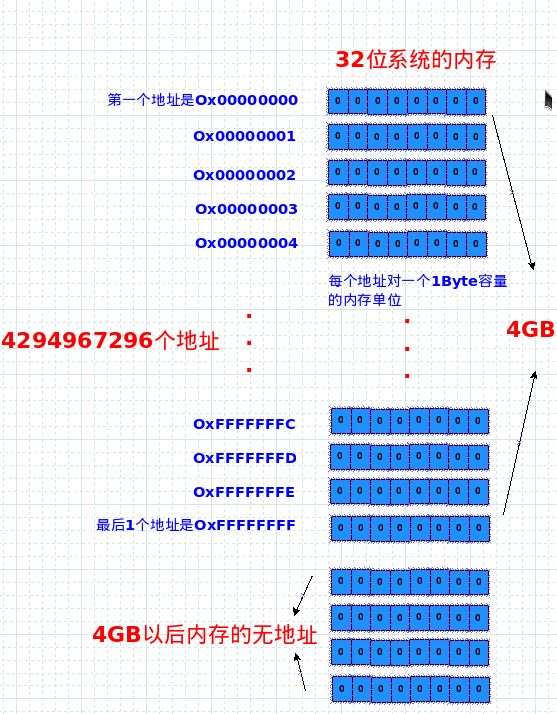
上面说了, 既然32位系统里内存地址长度是32位的. 所以32位的地址范围就是从 0000 0000 0000 0000 0000 0000 0000 0000 到 1111 1111 1111 1111 1111 1111 1111 1111 啦(Ox00000000 ~ OxFFFFFFFF),这里有几个地址呢?明显是有 2^32 个啦.
那么2^32到底是多少个? 2^32 = 4 * 1024(G) * 1024(M) * 1024(K) = 4294967296 , 就是4G啊, 而每1个地址对应1个1个字节,容量就是1byte,所以2^32个地址就总共能对应应4GB的内存容量啊,这里的B指的是byte 字节啊。
假如你给32位的系统配上了8GB的内存,操作系统最多也只能给其中4GB 分配地址,其余 4GB 是没有地址,因为地址不够用啊,所以32位系统最多支持4GB内存就是这样来的。
那么64位系统呢,对应地, 64位系统的内存地址是64位的二进制数啊, 0000 ...64个0 ~ 1111 ...64个1, 用十六进表示就是从Ox0000000000000000 ~ OxFFFFFFFFFFFFFFFF , 每个地址的长度比32位的长度多1倍!而64位系统总共有多少个地址?
2^64 = 2^34 * 2^10(G) * 2^10(M) * 2^10(K) 也就是 17179869184 G(4G × 4G)个地址,我艹这是神码概念,也就是说64位系统配上64位cpu理论上支持17多亿GB的内存,当然这个只是理论了,实际上现在的普通主版能上个16GB都不错了。
见下图:

9. 关于指针。
大家都知道指针是用来存放内存地址的,那么对于32位系统来讲,内存地址是1个32位长度的2进制数,而每1个内存单位长度只有1byte = 8bit(位),所以1个指针就需要4byte的内存来存放该指针的内容(1个内存地址)啦。
所以我们定义1个指针 int *p; 然后求sizeof(p) 是返回4的, 4字节嘛~
而对于64位系统来讲,内存地址是64位的2进制数,所以sizof(p)就返回8了,共需要8个内存单位去存放 64位系统的1个指针啊!