| 引言 |
| 声纳对目标进行主动探测估计时,通常会利用目标回波与发射信号的相似性对目标进行参数估计,而相关法就是最常用的方法。通过短副本与长回波的匹配确定副本形式的信号在回波中出现的位置,从而确定目标距离;并以不同频率的副本进行匹配估计速度。本文基于在DSP上实现主动自导信号检测算法(副本相关法)进行目标速度、距离的联合估计的项目背景介绍相关法的原理及其实现。(内容部分参考于本人硕士论文) |
一、处理思路:
通过对主动发射脉冲被目标反射的回波信号进行处理估计目标距离和速度。反射回波携带有目标信息,通过相关处理对比回波与发射波形的差别,通过波形差别解析出所携带的目标信息。
1、反射回波如何携带目标距离信息?
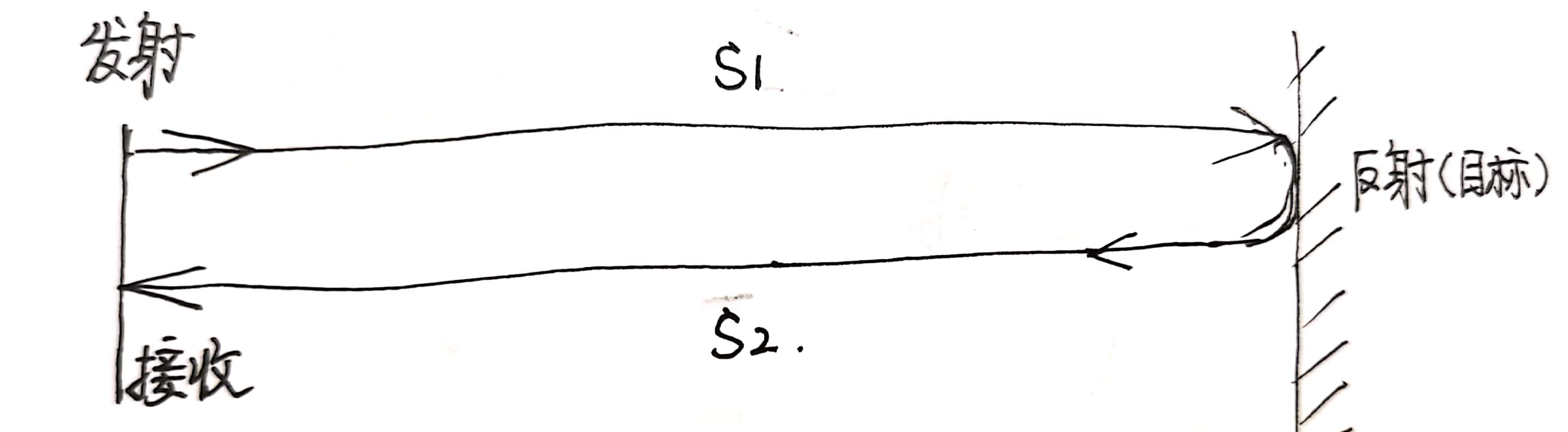
发射信号发射后要经过来回s=s1+s2两段路径才能被接收,即发射信号后要等待t0=s/v(v表示速度)这么长时间才能再次接收到信号。在回波信号上的体现就是信号中出现目标回波前的时延tao,如下图所示。
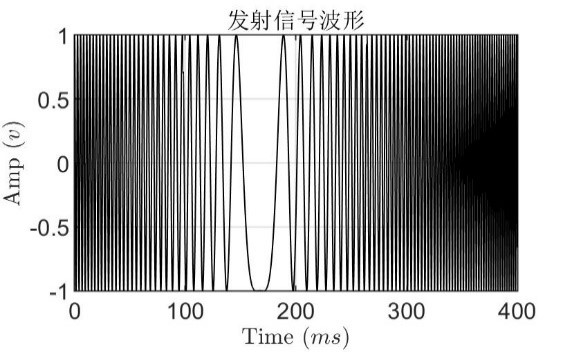
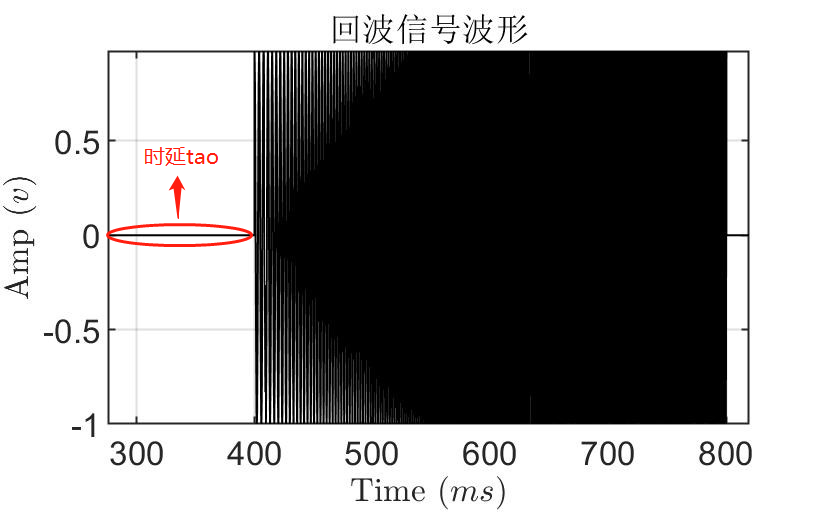
因此,只要提取出信号中时延tao便可以解算出反射点(目标)的距离。
2、反射回波如何携带目标速度信息?
通过多普勒效应将目标的速度信息映射在信号的频率上。通过多普勒频移(反射信号与发射信号的频差)解析目标的运动速度。
3、目标信息如何提取?
工程上有一个很常见且很精髓的处理思想—"试"。比如,我们不知道原信号的频率,可以拿不同频率的信号试着与原信号进行匹配(这个过程也叫作“扫描”),把试(匹配)的结果摆成一排就组成了频率响应,拿里面幅值(响应值)最大点的频率就近似代表原信号的频率(所谓的傅里叶分析),当然在试的时候由于拿来尝试匹配的样本数量(DFT点数)有限和原信号本身的信号长度有限会造成栅栏效益和截断效应(泄露)会导致各种估计误差(毕竟是试出来的,误差肯定有-_-!!),由此衍生出一系列的频域分析方法。另外,再比如波束形成(角度扫描)的波束(角度)响应,雷达信号MTD处理(多普勒频率扫描)里面多普勒频率响应等等都是依据这个思想。
那么,在此处回波的时延和多普勒频移能不能通过某种手段试出来呢?
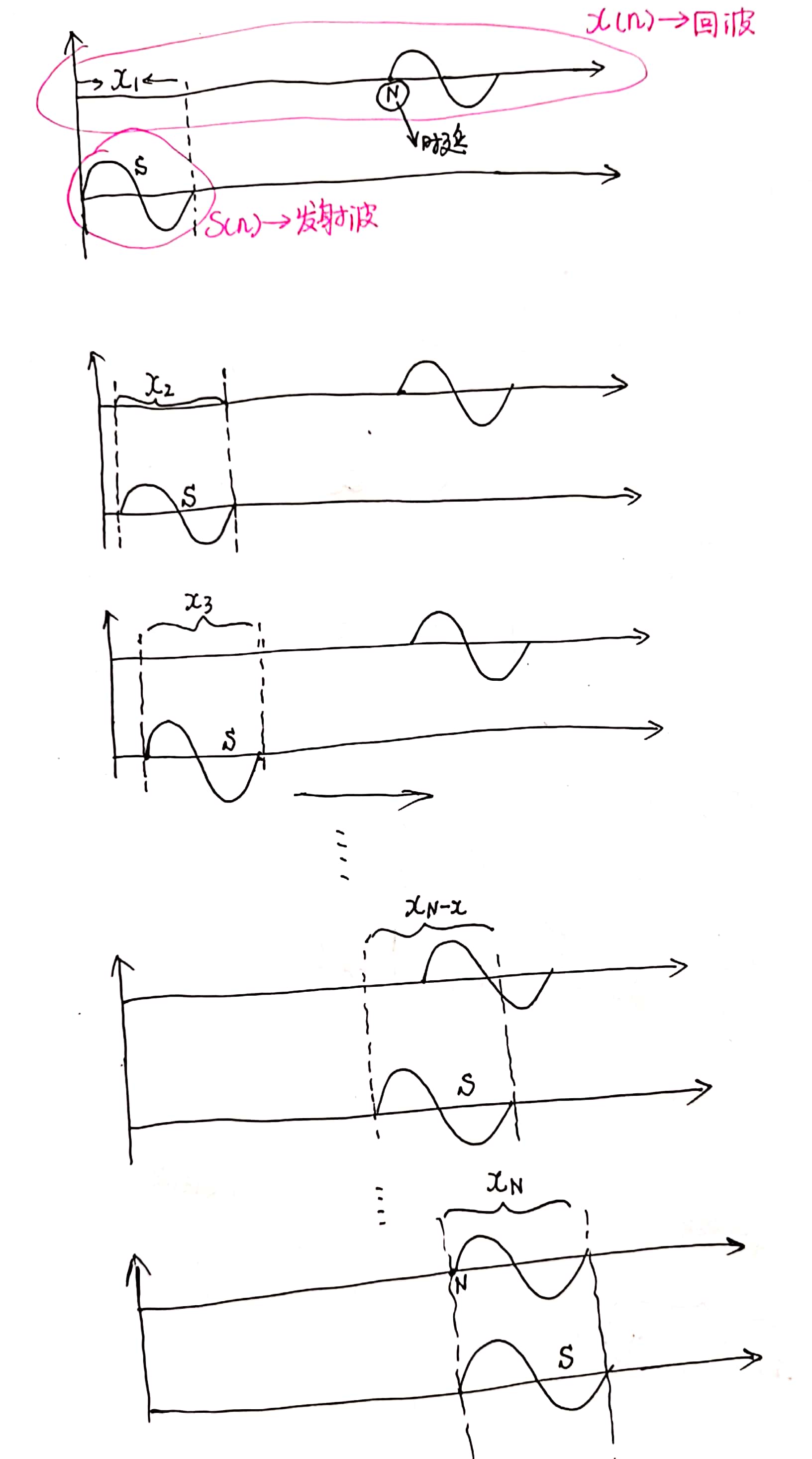
如上图所示,发射信号依次与回波信号中与发射信号长度一致的各个信号段(即x1、x2…xN…)进行匹配尝试,当发射信号与信号段波形越相似(匹配),则尝试出来的效果越好(幅值越大)。将原发射信号与各个回波信号段的匹配结果放在一起依次排列,就得出匹配滤波的结果,如下图所示。
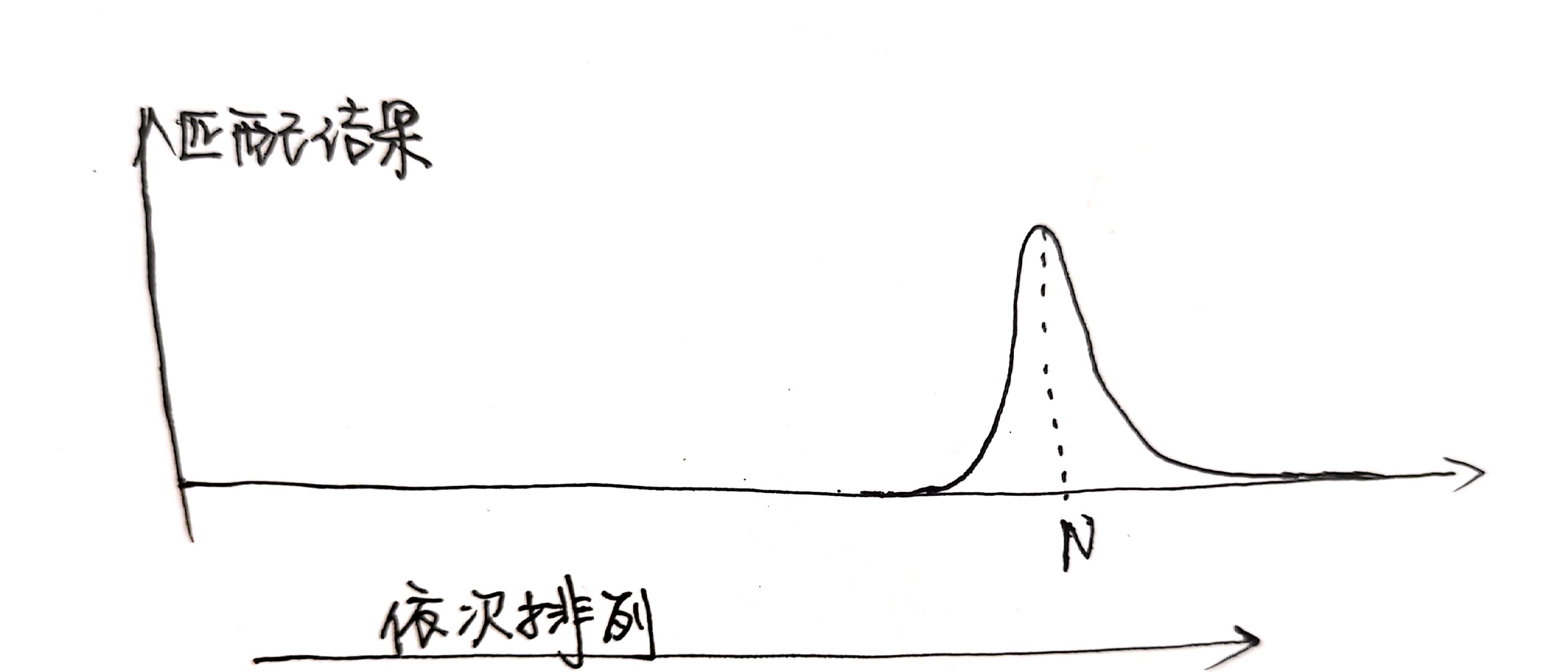
通过取其中匹配效果最好的那一次的信号段所在回波信号的位置的起始(即N)确定时延tao。
以上只说明回波中只有时延信息,没有多普勒信息(手画不好画)。那么多普勒频移怎么提取出来呢。
答案还是“试”。(假设目标回波与发射信号的差别只有多普勒频移)实现手段就是给原发射信号的很多副本加上不同的频移,拿这些加了频移的副本与目标回波试着匹配,最后取出响应最大的那一个副本,以它的频移代表目标回波的多普勒频移。
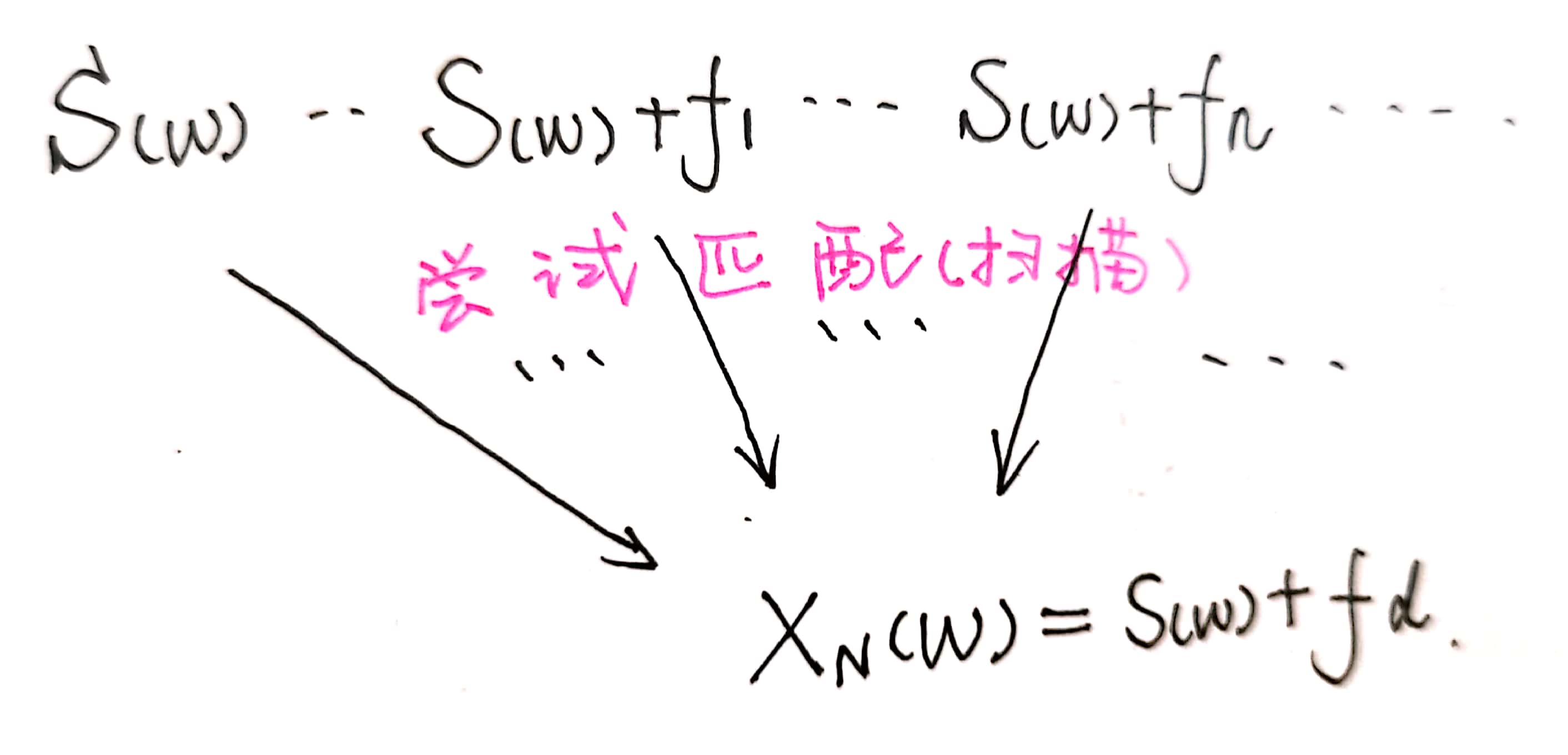
为了简化实现的逻辑,在进行时延匹配的时候,直接拿各个加了频移的发射信号副本与回波各个段进行匹配,这就实现了目标时延(距离)与多普勒(速度)的联合估计。需要注意的是由于多普勒效应在频率上产生多普勒频移时也会在时域上将信号的长度展宽或压缩(推导参考下图),这就造成了时延估计出现耦合误差,关于这一问题的处理在此不展开讨论。

二、处理流程:
上述内容主要描述了信息提取的方法,但没有具体说明如何实现“试”或者说匹配的过程。在数字信号处理领域对于匹配滤波的实现本质上就是两信号的互相关运算。用相关运算的结果表征匹配效果。所以估计时可采用发射信号副本与回波信号进行互相关计算,并提取出幅值最大点的时刻作为时延tao的值。处理流程如下所示。
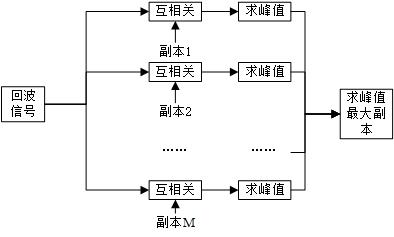
求出峰值即求目标回波与发射信号副本的匹配值;在这些峰值中求最大即求出目标回波与哪一个副本最匹配。找到这个最匹配的副本以它的频移近似代表多普勒频移,以这个副本估计出的时延近似代替真实的时延。(我们必须承认由于副本的个数和回波段的个数都是有限的,所以除极端情况外,误差一定存在。本质上,计算机只能进行有限的数据点(离散)的处理,所以结果都是近似的,存在误差的。)
二、工程要求:
通常目标检测和估计多应用于实时系统中,因此基于对处理速度考虑,算法在实现上,需要作出调整与优化,而本文所述的处理方法的计算瓶颈在互相关的运算上,因此相关处理的实现上要做出优化。此部分内容在后续的博客内容中阐明。
PS:由于本人水平有限,若上述内容中出现问题或表述不严谨的地方,还请各位大佬言明指正!