先来梳理一下我们之前所写的代码,原始的生成对抗网络,所要优化的目标函数为:
![]()
此目标函数可以分为两部分来看:
①固定生成器 G,优化判别器 D, 则上式可以写成如下形式:
![]()
可以转化为最小化形式:
![]()
我们编写的代码中,d_loss_real = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits = D_logits, labels = tf.ones_like(D))),由于我们判别器最后一层是 sigmoid ,所以可以看出来 d_loss_real 是上式中的第一项(舍去常数概率 1/2),d_loss_fake 为上式中的第二项。
②固定判别器 D,优化生成器 G,舍去前面的常数,相当于最小化:
![]()
也相当于最小化:
![]()
我们的代码中,g_loss = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(logits = D_logits_, labels = tf.ones_like(D))),完美对应上式。
接下来开始我们的 WGAN 之旅,正如 https://zhuanlan.zhihu.com/p/25071913 所介绍的,我们要构建一个判别器 D,使得 D 的参数不超过某个固定的常数,最后一层是非线性层,并且使式子:
![]()
达到最大,那么 L 就可以作为我们的 Wasserstein 距离,生成器的目标是最小化这个距离,去掉第一项与生成器无关的项,得到我们生成器的损失函数。我们可以把上式加个负号,作为 D 的损失函数,其中加负号后的第一项,是 d_loss_real,加负号后的第二项,是 d_loss_fake。
下面开始码代码:
为了方便,我们直接在上一节我们的 none_cond_DCGAN.py 文件中修改相应的代码:
在开头的宏定义中加入:
CLIP = [-0.01, 0.01]
CRITIC_NUM = 5
如图:

注释掉原来 discriminator 的 return,重新输入一个 return 如下:

在 train 函数里面,修改如下地方:


在循环里面,要改如下地方,这里稍微做一下说明,idx < 25 时 D 循环更新 25 次才会更新 G,用来保证 D 的网络大致满足 Wasserstein 距离,这是一个小小的 trick。
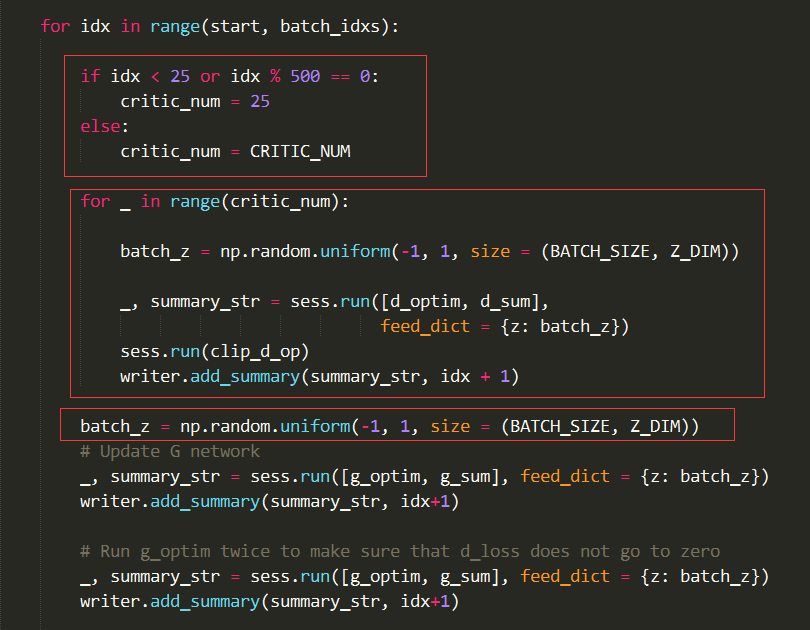
改完之后点击运行进行训练,WGAN 收敛速度很快,大约一千多次迭代的时候,生成网络生成的图像已经很像了,最后生成的图像如下,可以看到,图像还是有些噪点和坏点的。

最后的最后,贴一张网络的 Graph:

参考文献:
1. https://zhuanlan.zhihu.com/p/25071913