队列
队列是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。
顺序队列
建立顺序队列结构必须为其静态分配或动态申请一片连续的存储空间,并设置两个指针进行管理。一个是队头指针front,它指向队头元素;另一个是队尾指针rear,它指向下一个入队元素的存储位置。
每次在队尾插入一个元素时,rear增1;每次在队头删除一个元素时,front增1。随着插入和删除操作的进行,队列元素的个数不断变化,队列所占的存储空间也在为队列结构所分配的连续空间中移动。当front=rear时,队列中没有任何元素,称为空队列。当rear增加到指向分配的连续空间之外时,队列无法再插入新元素,但这时往往还有大量可用空间未被占用,这些空间是已经出队的队列元素曾经占用过得存储单元。
循环队列
在实际使用队列时,为了使队列空间能重复使用,往往对队列的使用方法稍加改进:无论插入或删除,一旦rear指针增1或front指针增1 时超出了所分配的队列空间,就让它指向这片连续空间的起始位置。自己真从MaxSize-1增1变到0,可用取余运算rear%MaxSize和front%MaxSize来实现。这实际上是把队列空间想象成一个环形空间,环形空间中的存储单元循环使用,用这种方法管理的队列也就称为循环队列。
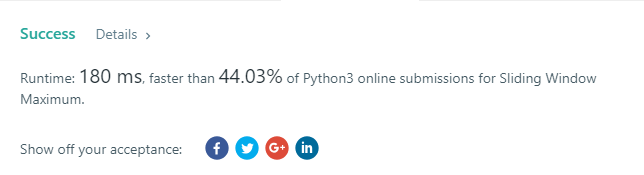
leetcode 239
代码实现
这道题用暴力求解不难,思路来得很快
class Solution:
def maxSlidingWindow(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
if len(nums) == 0:
return []
result = []
for i in range(len(nums) + 1 - k):
slide = nums[i:i+k]
result.append(max(slide))
return result
咋一看时间复杂度为O(n),要不是觉得Runtime太可疑我都没注意max()函数存在一个时间陷阱。这个方法真正的时间复杂度应该为O((l-k)n),l为nums长度,k即为所传入参数。无论如何,都很难达到理想的O(n)。
这时候才想起提示所说的双端队列。代码如下:
class Solution:
def pushUtilLg(self, queue, num):
"""
:type queue: List[int]
:rtype: List[int]
"""
try:
cmp_num = queue.pop()
while num > cmp_num:
cmp_num = queue.pop()
queue.append(cmp_num)
queue.append(num)
return queue
except:
return [num]
def maxSlidingWindow(self, nums, k):
"""
:type nums: List[int]
:type k: int
:rtype: List[int]
"""
if len(nums) == 0:
return []
if k == 1:
return nums
result = []
queue = []
for n in nums[:k]:
queue = self.pushUtilLg(queue, n)
for i in range(len(nums)+1-k):
n = nums[i+k-1]
queue = self.pushUtilLg(queue, n)
result.append(queue[0])
if nums[i] == queue[0]:
queue.pop(0)
return result
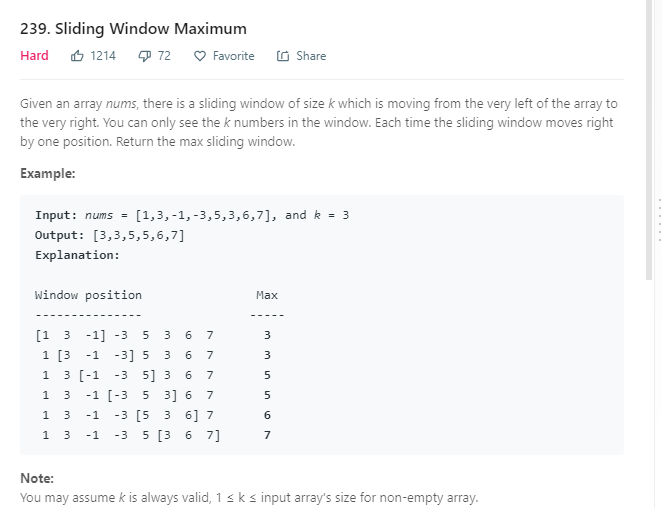
这里的关键是搞明白数字进队的规律,每个进队的数字,都要干掉比自己小的那些节点,我画了一幅示意图,如下: