神经网络
引言
这里我们集中讨论具有可调节权值的TLU网络。网络系统通过不断调节权值,直到其动作计算表现令人满意来完成学习。TLU网络称为神经网络是因为它模仿了生物神经元的一些特性。
训练单个TLU
1. TLU几何学
首先介绍如何训练单个TLU权值,从而使其对某一些训练集合产生正确的输出。

2. 扩充向量

神经网络
首先简要介绍下神经网络。神经网络的每个单元如下:
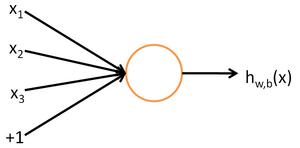
其对应的公式如下:
![]()
其中,该单元也可以被称作是Logistic回归模型。当将多个单元组合起来并具有分层结构时,就形成了神经网络模型。下图展示了一个具有一个隐含层的神经网络。
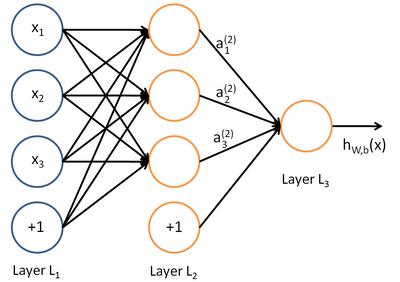
其对应的公式如下:

![]()
比较类似的,可以拓展到有2,3,4,5……个隐含层。
神经网络的训练方法采用反向传播算法,为了更好地描述反向传播算法,这里要定义一个十分简单的双层神经网络,它的结构如下图所示。

-
输入的数据是2维。
-
第一层神经网络的输入也是2维,输出是4维,非线性部分采用sigmoid函数。
- 第二层神经网络的输入也是2维,输出是1维,非线性部分采用sigmoid函数。
如果把神经网络的计算过程拆解成一个个的部分,那么它的计算过程就变成了下面这些步骤的组合。

求导的过程需要将上述列出的步骤反向进行。首先是第二层网络计算公式反推:

到这里我们已经顺利的求出了第二层的所有参数的导数了。下面是第一层网络的计算公式反推。
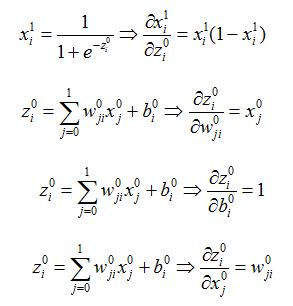
到这里,基本运算已经准备完成。而且随着模型从高层网络向低层网络反向计算,那些已经计算好的中间结果也可以用于计算低层参数的梯度。所以经过整理,全部的计算过程可以如下表示:

![]()
以上就是计算的全过程了,以上9个步骤可以分成3个部分。
-
第1步完成了模型输出值的梯度计算。
-
第2-5步完成了第二层神经网络的梯度计算。
-
第6-8步完成了第一层神经网络的梯度计算。
如果从更具体的角度来看每一层神经网络的反向计算内容,就会发现他们都完成了下面的梯度计算:

了解了这个模式,神经网络计算梯度模块化这件事就变得容易许多。在前向计算时,每一层使用同样的计算流程产生输出,并传给后一层作为输入;同样在反向传播时,每一层也使用同样的流程,计算上面4个值,把梯度反向传给前一层的输出。这样,每一个全连接层之间的运算变得相对独立。