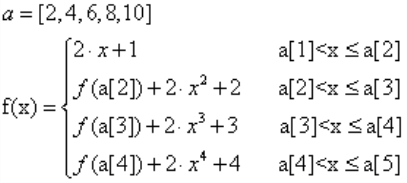使用matlab表示“段数不确定”的分段函数

示例函数：

分段函数f(x)的段数为数组a的长度减1，在表达f(x)时，不能直接使用a的长度5-1=4.

方法1：

先计算每个间隔点的函数值f(a2),f(a3),f(a4),再循环表示f(x)。

f(x) = (2x+1).*(x>2&&x<=4)

+(f(4)+2x^2+2).*(x>4&&x<=6)

+(f(6)+2x^3+3).*(x>6&&x<=8)

+(f(8)+2x^4+4).*(x>8&&x<=10)

因为每段中的表达式有一定的规律，所以可以用循环进行表示。

代码如下：

function y =f(x)

y = 0;
a = [2 4 6 8 10];
% gap vector is used to store f(a1),f(a2),...,f(a5)
gap = zeros(size(a));
for i = 2:length(a)
    gap(i) = 2*(a(i)^(i-1))+(i-1);
end
for i = 2:length(a)
    gap(i) = gap(i) + gap(i - 1);
end

% The representation of piecewise function 
for i = 1:length(a)-1
    y = y + (gap(i) + 2*(x^i)+i).*(x>a(i)&&x<=a(i+1));
end

方法2：

同方法1，先计算间隔点函数值f(a2),f(a3),f(a4),再使用插值函数判断输入的自变量x位于哪个区间，进而使用该区间上的表达式。

代码如下：

function y = f(x)

a = [2 4 6 8 10];

% 计算每个区间的基数f(a2),f(a3),f(a4)
gap=zeros(size(a));
gap(1)=0;gap(end)=nan;
for i=2:length(a)-1
    gap(i)=gap(i-1)+2*a(i)^(i-1)+(i-1); 
end

%使用插值函数计算x落在哪个区间上，num表示段数。
num=interp1(a,1:length(a),x);  
num=ceil(num)-1;              
num(isnan(num))=length(a);     %处理超过数组a范围的值
num(num==0)=1;                      %处理第一个x = a(1)

%计算函数值，每个分段上的基数加上该分段上的变量
y=gap(num)+2*x.^num+num;  

方法3：

同方法2，但不使用插值函数，使用Find函数判断输入的自变量x位于哪个区间

代码如下：

function y = f(x)

a = [2 4 6 8 10];

% 计算每个区间的基数f(a2),f(a3),f(a4)
gap=zeros(size(a));
gap(1)=0;gap(end)=nan;
for i=2:length(a)-1
    gap(i)=gap(i-1)+2*a(i)^(i-1)+(i-1); 
end

%使用find函数计算x落在哪个区间上，num表示段数。
num=find(sort([a x]) == x);
num=num(1)-1;     % 当a中某元素与x相同时，取第一个。
num(isnan(num))=length(a);     %处理超过数组a范围的值
num(num==0)=1;                      %处理第一个x = a(1)

%计算函数值，每个分段上的基数加上该分段上的变量
y=gap(num)+2*x.^num+num;  

参考资料：

matlab分段+递归函数的表示方法

matlab分段函数表示，分段数为变量，不是常量