0 - 人体姿态识别存在的挑战
- 图像中的个体数量、尺寸大小、位置均未知
- 个体间接触、遮挡等影响检测
- 实时性要求较高,传统的自顶向下方法运行时间随着个体数越多而越长
1 - 整体思路
整个模型架构是自底向上的,先识别出关键点和关节域,然后通过算法组合成个体的姿势图。
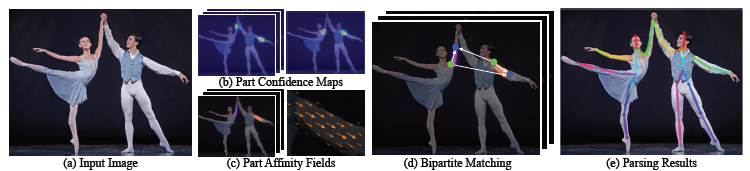
1.1 - 求所有关键点(头部,肩膀,手肘,手腕...)
- 第一个CNN将原图所为输入,输出热图(每一个热图包含一种特定关键点)
- 第二个CNN将第一个CNN的输出(热图)和原图作为输入,输出热图
循环直到收敛。示意图如上图(b)所示。
1.2 - 求所有关联区域
- 第一个CNN将原图作为输入,输出是热图(每一个热图包含某一种特定的连接区域)
- 第二个CNN将第一个CNN的输出(热图)和原图作为输入,输出热图
循环直至收敛。示意图如上图(c)所示。
(注:上述的热图是为了便于了解整体流程,其对应于下面详细描述的置信图或者PAFs)
1.3 - 根据关键点和关联区域进行矢量连接
由上述两步得到的关键点和关联区域,而后需要依据关联区域将关键点连接以组成人体真正的骨骼结构。如果全局的每对点都试验一遍然后找到最优的划分和组合结构,是一个NP难问题。因此作者提出了以一个最小限度的边数量来获得个体姿势的生成树图(用了二分图+匈牙利算法等),在保证不错的准确度的同时,大大减少了复杂度,提高了实时性。
2 - 具体方法
将输入图像通过上述两个分支,得到关键点(confidence maps,集合$S$)和关联区域(PAFs,集合$L$)。而后便是一个匹配问题,将其划分为二分图再运用匈牙利算法使得边权最大从而构出个体姿态。
2.1 - 架构
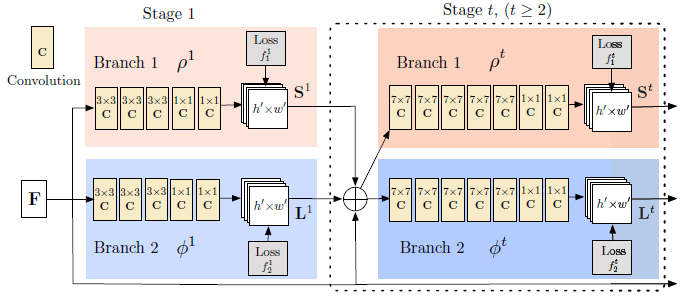
原图经过VGG-19得到F(feature maps),然后经过上下分支,每个分支有t个阶段(表示越来越精细),每个阶段将feature maps进行融合。
2.2 - 损失函数定义
通过不同损失函数引导不同分支做不同预测任务。
$$f_S^t = \sum_{j=1}^{J}\sum_{P}W(p)\cdot \left \| S_j^t(P)-S_j^*(p) \right \|_2^2$$
$$f_L^t = \sum_{c=1}^{C}\sum_{P}W(p)\cdot \left \| L_c^t(P)-L_c^*(p) \right \|_2^2$$
$$f=\sum_{t=1}^{T}(f_S^t+f_L^t)$$
2.3 - 个体区域检测置信图
置信图由ground truth的关键点生成,每一个置信图都是对特定关键点的2D表示(如果图像中有$j$个对应关键点可见,则应该有$j$个峰值)。置信图可以理解为图像该点属于对应关键点的概率。
对于第$k$个人产生部位$j$的置信图蔓延程度$S_{j,k}^*(p)=exp\left (-\frac{\left \| p-x_{j,k} \right \|^2_2}{\sigma^2}\right )$,其中$p$表示图像中的坐标,那么总的置信图(多个个体)为$S_j^*(p)=\mathop{max}\limits_{k}S^*_{j,k}(p)$。
2.4 - PAFs(部位联系场)

PAFs是一个2D矢量场,保留了位置和方向。如果坐标$P$在这个肢体上面,则值为$j_1$指向$j_2$的单位矢量,否则为零向量。
$$L_{c,k}^*(p)=\begin{cases} v\ if\ p\ on\ limb\ c,k\\ 0\ otherwise \end{cases}$$
其中,对应的单位向量由下式得到:
$$v=(x_{j_2,k}-x_{j_1,k})/\left \| x_{j_2,k}-x_{j_1,k} \right \|$$
通过下式定义肢体上的点:
$$0 \leq v \cdot (p-x_{j_1,k}) \leq l_{c,k} \ and \ \left | v_{\perp} \cdot (p-x_{j_1,k}) \right | \leq \sigma_l$$
其中,肢体宽度$\sigma_l$是像素级上的距离,肢体长度$l_{c,k}=\left \| x_{j_2,k}-x_{j_1,k} \right \|_2$,并且$v_{\prep }$是正交于$v$的向量。
一张图像中肢体$c$的PAFs通过下式计算:
$$L_c^*(p)=\frac{1}{n_c(p)}\sum_{k}L_{c,k}^*(p)$$
(此处存疑问:多个人的PAFs必定不同,这样子平均难道不会削弱精确度吗?还是因为这种情况很少出现而做得一个满足模型简易性的让步?)
根据预测出来的PAFs沿着候选区域计算两个关键点之间的线积分。对于两个候选部位位置$d_{j_1}$和$d_{j_2}$,我们从PAFs中取样,$L_c$表示的是沿着线段去衡量它们间联系的置信度:
$$E=\int_{u=0}^{u=1}L_c(p(u))\cdot \frac{d_{j_2}-d_{j_1}}{\left \| d_{j_2}-d_{j_1} \right \|_2}du,\ (10)$$
其中$p(u)$是在两个身体部位$d_{j_1}$和$d_{j_2}$间插入的位置:
$$p(u)=(1-u)d_{j_1}+ud_{j_2}.\ (11)$$
实际上,我们通过抽样和求和等间距的$u$的值来近似积分。
2.5 - 多人PAFs
如果图像中有多个个体,那么识别出来的多个关键点需要划分为多个个体,算法的目标事找到所有最佳的关联,用如下集合表示:
$$Z = \{z_{j_1j_2}^{mn}\ :\ for\ j_1,j_2 \in \{1...J\},m \in \{1...N_{j_1}\},n \in \{1...N_{j_2}\}\}$$
考虑一对关键点$j_1$和$j_2$(如脖子、右臂)组成的肢体$c$,可以抽象层二分图问题,其中节点为候选集合,边的权重由上面积分公式计算,二分图匹配选择最大权重的边,使得没有共享结点。
$$\begin{matrix}\mathop{max}\limits_{Z_c}E_c=\mathop{max}\limits_{Z_c}\sum_{m \in D_{j_1}}\sum_{n \in D_{j_2}}E_{mn}\cdot z_{j_1j_2}^{mn},\ (12)\\s.t.\ \forall m \in D_{j_1}, \sum_{n \in D_{j_2}}z_{j_1j_2}^{mn} \leq 1,\ (13)\\\forall n \in D_{j_2}, \sum_{n \in D_{j_2}}z_{j_1j_2}^{mn} \leq 1,\ (14)\end{matrix}$$
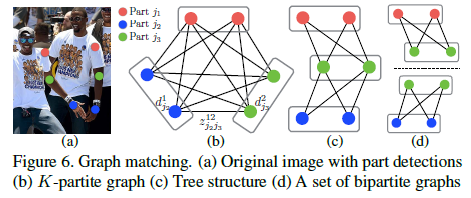
2.6 - 两个松弛(还没理解透,待补充)
- 选择一个最小限度的边数量去获得一个个体姿势生成树概要而不是使用全图
- 进一步分解匹配问题为一个集合的二分图匹配子问题并且独立地在相邻树解决匹配问题
3 - 结果
准确率高,实时性好。且贪心策略可行,效率高很多,效果也更好。

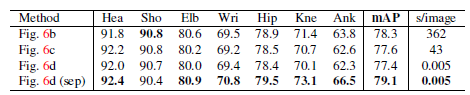
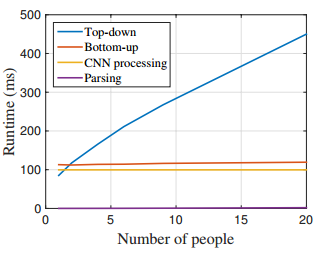
自底向上方法的运行时间几乎不随个体数量的增加而增加。运行时间主要包括两个部分:(1)CNN处理时间,其运行复杂度为$O(1)$而不管什么数量的个体;(2)多个体解析时间的运行复杂度为$O(n^2)$,其中n表示个体数量。然而,解析时间并不会很是影响整体时间,因为它比CNN处理时间小了两个数量级,例如,对于9个个体,解析用了0.58ms而CNN用了99.6ms。我们的方法对于有19个个体的视频达到了8.8fps的速度。
4 - 存在挑战

我们的方法的准确率低于对较小尺度($AP^M$)的个体的自顶向下方法。其原因是我们的方法需要处理在所有个体在一张图片的一个对焦中的更大的范围尺度。相反,自顶向下方法能够将每一个检测区域放缩到一个更大的尺寸因此相比小尺度受到更少的影响。
5 - 补充知识点
5.1 - 非极大值抑制
- 将所有框按照得分排序,选中最高分的框
- 遍历其它框,如果和当前最高分框的重叠面积(IOU)大于一定阈值,删除之
- 从未处理的框中继续选择得分最高的,重复上述过程
最后获得各个待检测区域最佳的检测框。
5.2 - 匈牙利算法
在我的另一篇博客中有详细解析。
6 - 参考资料
https://blog.csdn.net/yxr403614258/article/details/77977330